Method by Lanczos
The eigenvalues are determined directly. Using this algorithm, rapid convergence can usually be achieved. This method is suitable for standard models and is therefore set by default.
More Information: Lanczos Method
Roots of Characteristic Polynomial
This method is also based on a direct calculation method. For larger structural systems, this method can be faster than the Lanczos method. The main advantage is the accuracy of the calculation of higher eigenvalues.
More Information: Characteristic Polynomial
Subspace Iteration Method
All eigenvalues are determined in one step. The spectrum of the stiffness matrix has a strong influence on the duration of the calculation. Since the stiffness matrix is stored in the operating memory, this method is not suitable for complex systems. Furthermore, negative critical load factors may be displayed.
More Information: Krylov Subspace Method
ICG Iteration Method
The Incomplete Conjugate Gradient method requires little random access memory. Since the eigenvalues are determined one after the other, this requires more computing time for the calculation of small to medium structural systems, in comparison with the direct method. However, the spectrum has no influence on the calculation duration. The ICG method is suitable for analyses of very large systems with few eigenvalues. This method does not provide any negative critical load factors.
More Information: CG Method













.png?mw=350&hash=c6c25b135ffd26af9cd48d77813d2ba5853f936c)

























.png?mw=512&hash=831a9308cb08f34e4734dfdce7c09ccf15f76cb6)





_1.jpg?mw=350&hash=ab2086621f4e50c8c8fb8f3c211a22bc246e0552)





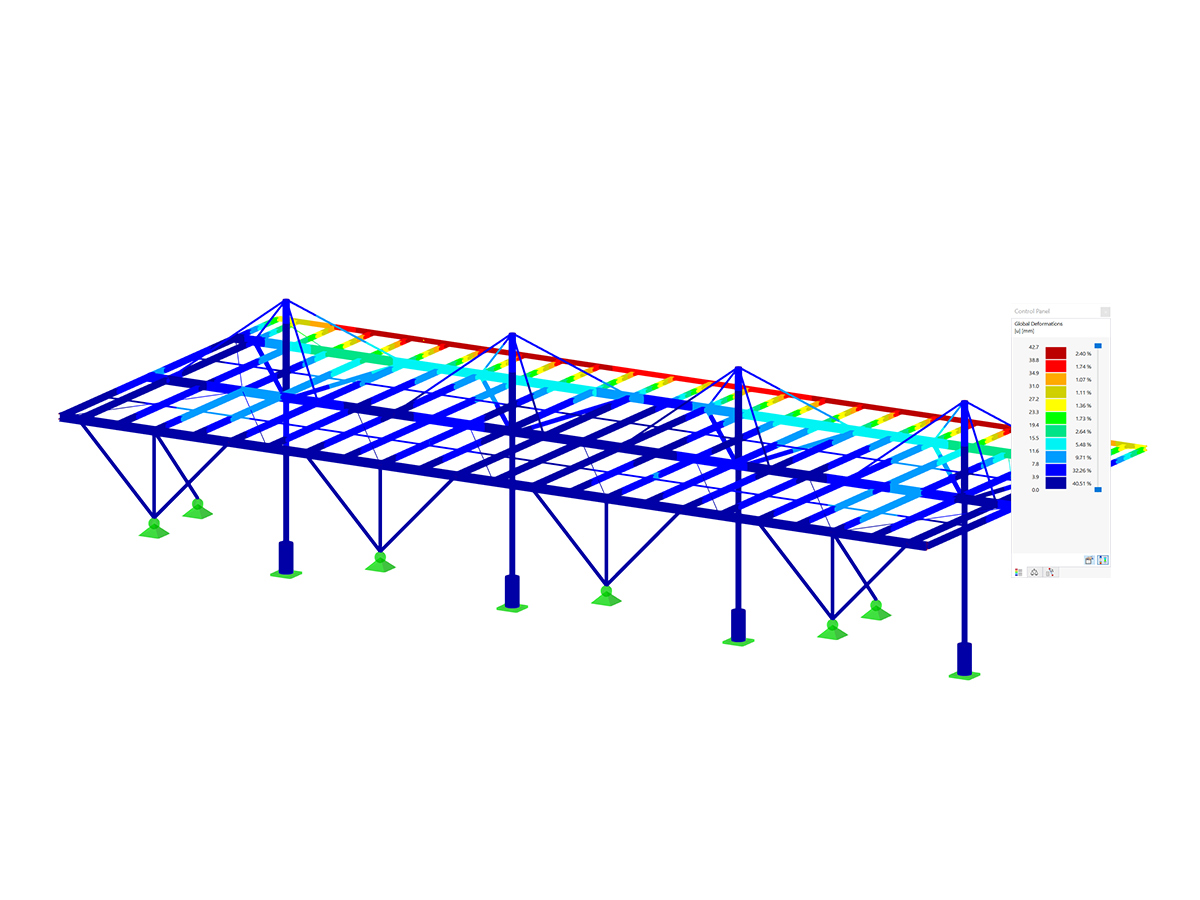
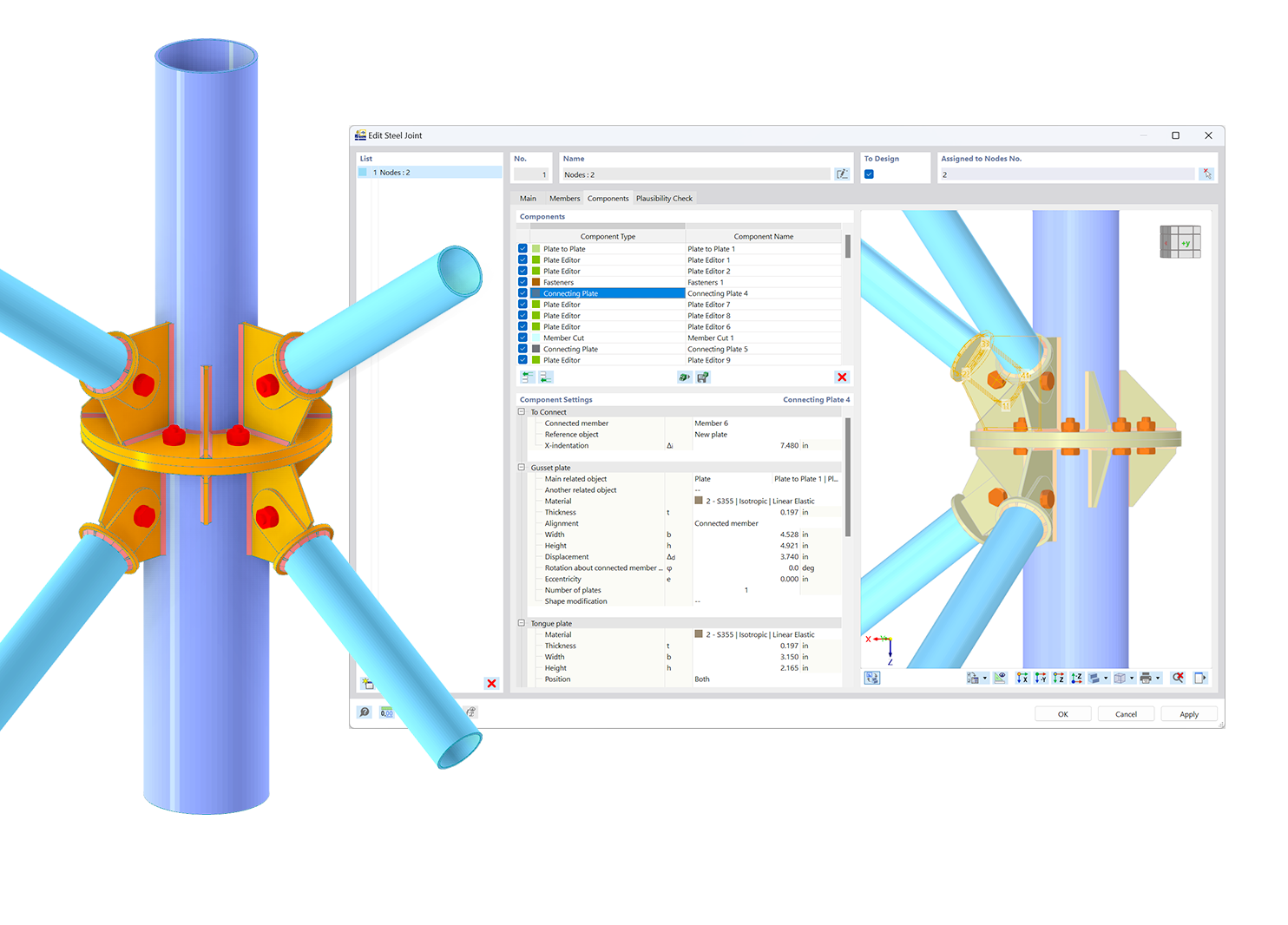.png?mw=600&hash=49b6a289915d28aa461360f7308b092631b1446e)