36x

2024-09-24

VE0063 | Centrifugal Force Loading

Description

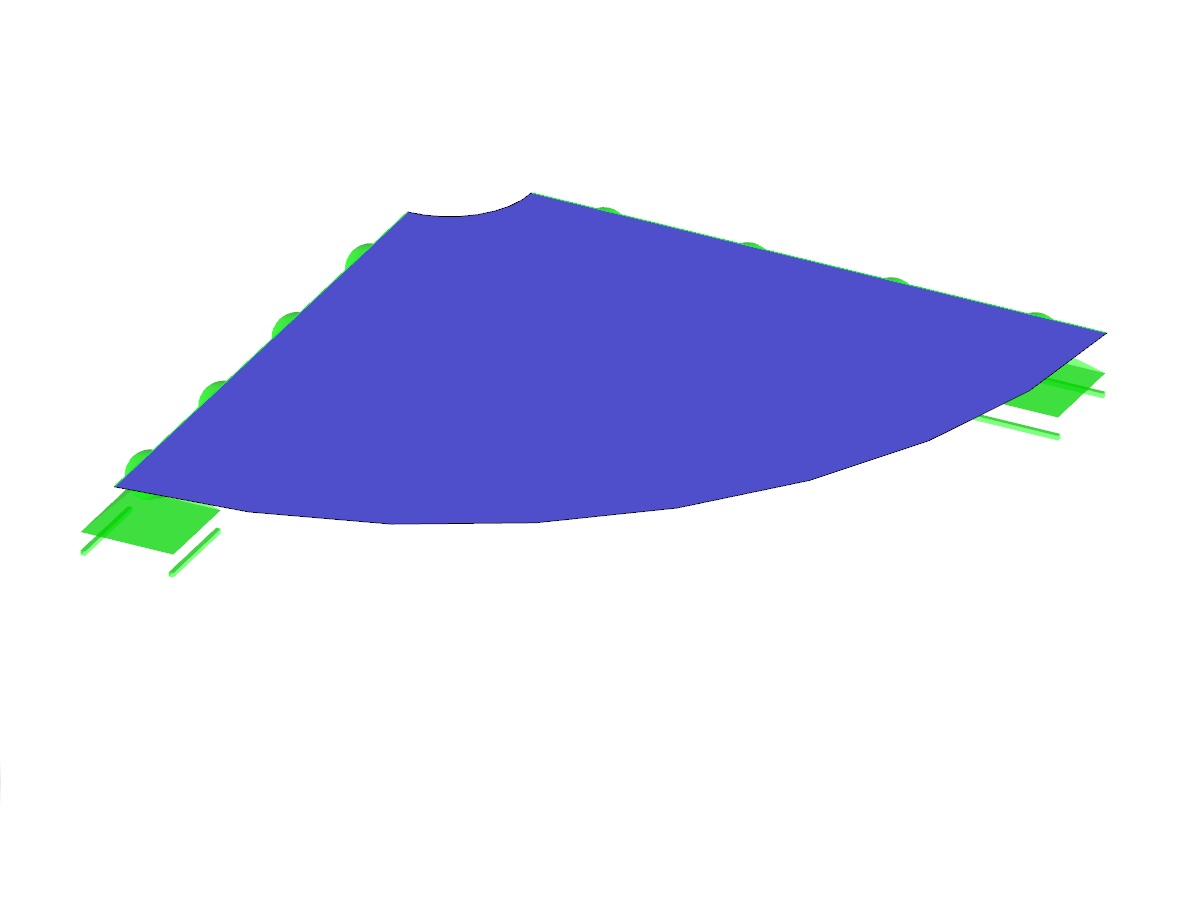
A compact disc (CD) rotates at a speed of 10,000 rpm. Therefore, it is subjected to centrifugal force. The problem is modeled as a quarter model. Determine the tangential stress σ_t on the inner and outer diameters and the radial deflection u_r of the outer radius.

Material	Polycarbonate	Modulus of Elasticity	E	850.000	MPa
		Poisson´s Ratio	ν	0.300	-
		Density	ρ	1190.000	kg/m³
Geometry		Inner Radius	r₁	7.500	mm
		Outer Radius	r₂	60.000	mm
		Thickness	t	1.200	mm
Load		Rotary Motion	ω	1047.200	rad/s

Centrifugal Force Loading

Analytical Solution

The tangential stress σ_t and radial stress σ_r on a thin rotating disc is defined as follows:

σ_{t} (r) = C_{1} + \frac{C_{2}}{r^{2}} - \frac{1 + 3 ν}{8} {ρω}^{2} r^{2}

C₁, C₂

Real constants based on boundary conditions

Tangential Stress on Thin Rotating Disc

σ_{r} (r) = C_{1} + \frac{C_{2}}{r^{2}} - \frac{3 + ν}{8} {ρω}^{2} r^{2}

C₁, C₂

Real constants based on boundary conditions

Radial Stress on Thin Rotating Disc

where C₁ and C₂ are real constants, which can be obtained from the boundary condition of zero radial stress σ_r both on the inner and outer diameter. The radial deflection of the outer radius can be calculated using the Hooke's Law.

u_{r} (r_{2}) = \frac{r_{2}}{E} [σ_{t} (r_{2}) - {νσ}_{r} (r_{2})]

Radial Deflection of Disc Outer Radius

RFEM Settings

Modeled in RFEM 5.06 and RFEM 6.06
The element size is l_FE = 1.000 mm
Isotropic linear elastic material model is used
Kirchhoff plate bending theory is used

Results

RFEM 6 Results – von Mises Stress

Quantity	Analytical Solution	RFEM 6	Ratio	RFEM 5	Ratio
σ_t(r₁) [Nmm^-2]	3.889	3.891	1.001	3.891	1.001
σ_t(r₂) [Nmm^-2]	0.883	0.882	0.999	0.882	0.999
u_r(r₂) [mm]	0.0623	0.0623	1.000	0.0623	1.000

423x

15x

Verification Example 000063 | 1

;