Pokud aktivujete funkci Nelineární chování materiálu na (vyžaduje licenci) v Model – základní údaje, jsou v seznamu materiálových modelů kromě možnosti "Izotropní | lineárně elastického' a 'Ortotropního | Lineárně elastický' v seznamu materiálových modelů k dispozici další možnosti.
Pokud v programu RFEM používáte nelineární materiálové modely, provádí se vždy iterační výpočet. V závislosti na materiálovém modelu je definována patřičná závislost napětí a přetvoření.
Tuhost konečných prvků se v průběhu iterací znovu a znovu upravuje, aby byl dodržen vztah mezi napětím a přetvořením. Úprava se vždy provádí pro celou plochu nebo těleso. Bei der Auswertung der Spannungen sollte deswegen immer die Glättungsart Konstantní v prvcích sítě .
Některé materiálové modely jsou v programu RFEM označeny jako 'plastické', jiné jako 'nelineárně elastické'.
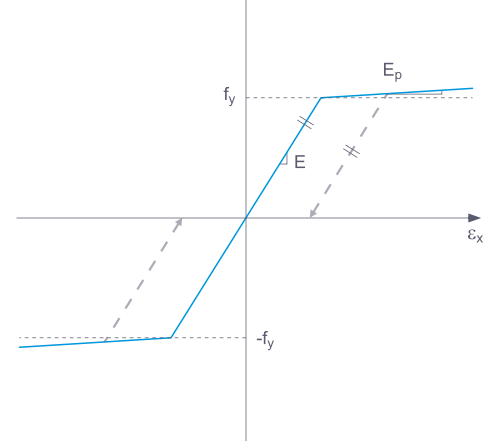
Pokud se konstrukční prvek z nelineárně elastického materiálu opět odlehčí, vrátí se přetvoření stejnou cestou zpět. Při úplném odlehčení nezůstává žádné přetvoření.
Při odlehčování konstrukčního prvku s plastickým materiálovým modelem zůstává po úplném odlehčení zbytkové přetvoření.
Die Be- und Entlastung kann mit dem Add-On Analyse von Bauzuständen simuliert werden.
Základní informace o nelineárních materiálových modelech najdete v odborném článku Podmínky plasticity v izotropním nelineárním elastickém materiálovém modelu.
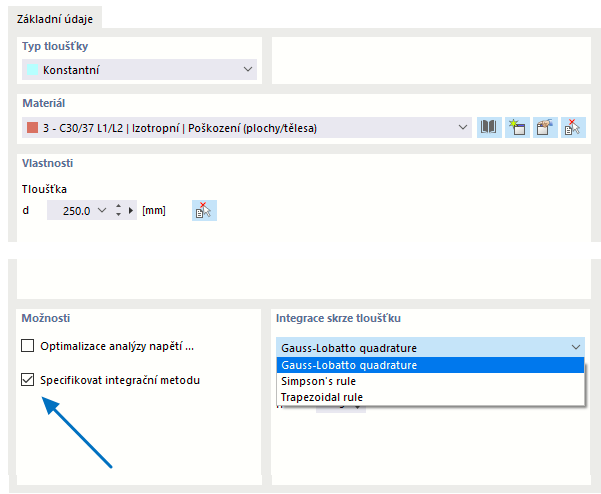
Die Schnittgrößen in Platten mit nichtlinearem Material ergeben sich aus der numerischen Integration der Spannungen über die Plattendicke. Um die Integrationsmethode für die Dicke festzulegen, haken Sie im Dialog 'Dicke bearbeiten' die Option Integrationsmethode angeben an. Damit stehen folgende Integrationsmethoden zur Auswahl:
- Gaussova-Lobattova kvadratura
- Simpsonovo pravidlo
- Lichoběžníkové pravidlo
Des Weiteren können Sie die 'Anzahl der Integrationspunkte' über die Plattendicke von 3 bis 99 vorgeben.
Izotropní plastický (pruty)
Wenn Sie in der Dropdown-Liste 'Materialmodell' den Eintrag Isotrop | Plastický (pruty), vytvoří se záložka pro zadání nelineárních materiálových parametrů.
V této záložce zadejte závislost napětí-přetvoření. K dispozici jsou následující možnosti:
- Normovaný
- Bilineární
- Graf
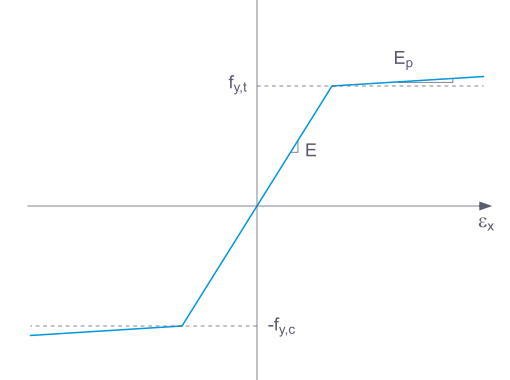
Pokud zvolíte Základní, RFEM použije bilineární materiálový model. Für den Elastizitätsmodul E und die Fließgrenze fy werden die Werte aus der Materialdatenbank genutzt. Aus numerischen Gründen verläuft der Ast nicht genau horizontal, sondern hat einen kleinen Anstieg Ep.
Pokud chcete změnit hodnoty meze kluzu a modulu pružnosti, zaškrtněte v záložce 'Základní údaje' volbu Uživatelsky zadaný materiál.
Bei der bilinearen Definition können Sie auch den Wert für Ep eingegeben.
Složitější vztahy mezi napětím a přetvořením lze definovat pomocí Pracovního diagramu. Pokud zaškrtnete tuto možnost, zobrazí se záložka 'Pracovní diagram'.
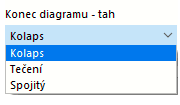
V každém řádku definujte bod pro závislost napětí-přetvoření. V seznamu 'Konec diagramu' pod diagramem můžete vybrat, jak má diagram pokračovat za posledním definičním bodem:
V případě možnosti 'Kolaps' spadne napětí za posledním definičním bodem zpět na nulu. 'Tečení' znamená, že napětí zůstane konstantní s rostoucím přetvořením. 'Spojitý' znamená, že křivka pokračuje se sklonem stejným jako mezi posledními body.
Izotropní plastický (plochy/tělesa)
Wenn Sie in der Dropdown-Liste 'Materialmodell' den Eintrag Isotrop | Plastický (plochy/tělesa), vytvoří se záložka pro zadání nelineárních materiálových parametrů.
Nejprve vyberte 'Hypotézu porušení od napětí' (pevnostní hypotézu). Můžete si vybrat z následujících hypotéz:
- von Mises (energetická hypotéza)
- Tresca (hypotéza max. smykového napětí)
- Drucker-Prager
- Mohr-Coulomb
Pokud vyberete von Mises, použije se v pracovním diagramu následující napětí:
Plochy:
Tělesa:
Podle Trescovy hypotézy se použije následující napětí:
Plochy:
Tělesa:
Podle Druckerovy-Pragerovy hypotézy se pro plochy a tělesa použije následující napětí:
Podle Mohrovy-Coulombovy hypotézy se pro plochy a tělesa použije následující napětí:
Izotropní nelineárně elastický (pruty)
Funkčnost do značné míry odpovídá materiálovému modelu Izotropní plastický (pruty). Na rozdíl od něj však po odlehčení napětí nedochází k žádné plastické deformaci.
Izotropní nelineárně elastický (plochy/tělesa)
Funkčnost do značné míry odpovídá materiálovému modelu Izotropní plastický (plochy/tělesa). Na rozdíl od něj však po odlehčení napětí nedochází k žádné plastické deformaci.
Izotropní Poškození (plochy/tělesa)
Na rozdíl od jiných materiálových modelů není pracovní diagram pro tento materiálový model antimetrický vzhledem k počátku. Tímto způsobem lze například modelovat chování drátkobetonu. Podrobné informace o modelování drátkobetonu naleznete v odborném článku Stanovení materiálových vlastností drátkobetonu.
U tohoto materiálového modelu je izotropní tuhost redukována skalárním parametrem poškození. Tento parametr poškození se stanoví na základě průběhu napětí, které je definováno v diagramu. V tomto případě se nezohledňuje směr hlavních napětí, ale dochází k poškození ve směru srovnávacího poměrného přetvoření, které zahrnuje také třetí směr kolmý na rovinu. Tahové a tlakové oblasti tenzoru napětí jsou řešeny odděleně. V každém případě platí různé parametry poškození.
Velikost "referenčního prvku" určuje, jak se má přetvoření v oblasti trhlin přizpůsobit délce prvku. Při přednastavené nulové hodnotě nedochází ke změně měřítka. Tímto způsobem se téměř realisticky modeluje materiálové chování drátkobetonu.
Teoretické základy materiálového modelu 'Izotropní Poškození' najdete v odborném článku Nelineární materiálový model Poškození.
Ortotropní plastický (plochy) / Ortotropní plastický (tělesa)
Materiálový model Tsai-Wu propojuje plastické a ortotropní vlastnosti. To umožňuje speciální modelování materiálů s anizotropními vlastnostmi, jako jsou plasty vyztužené vlákny nebo dřevo.
Při plastizaci materiálu zůstávají napětí konstantní. Dochází k jejich redistribuci v závislosti na tuhosti v jednotlivých směrech.
Der elastische Bereich entspricht dem Materialmodell Ortotropní lineárně elastický (tělesa) . Pro plastickou oblast platí následující podmínka plasticity podle Tsai-Wu:
Plochy (2D):
Tělesa (3D):
Veškeré pevnosti je třeba zadat jako kladné hodnoty.
Podmínku plasticity si můžeme představit jako plochu ve tvaru elipsy v šestirozměrném prostoru napjatosti. Pokud se jedna z daných tří složek napětí uvažuje jako konstantní hodnota, lze plochu promítnout do trojrozměrného prostoru napjatosti.
Ist der Wert für fy(σ) nach Gleichung Tsai-Wu, ebener Spannungszustand kleiner als 1, so liegen die Spannungen im elastischen Bereich. Plastická oblast je dosažena, jakmile fy (σ) = 1. Hodnoty větší než 1 nejsou přípustné. Chování modelu je ideálně plastické, tzn. nedochází k žádnému zpevnění.
Zdivo
Wenn bei den Modell-Basisangaben das Bemessungs-Add-On Mauerwerksbemessung aktiviert ist (Lizenz erforderlich), stehen für den Materialtyp 'Mauerwerk' die Materialmodelle 'Isotrop | Zdivo | Plastisch (Flächen)' und 'Orthotrop | Zdivo | Plastický (plochy)'.
Oba materiálové modely jsou popsány v kapitole Materiály manuálu pro Posouzení zdiva.