Vérification des poutres en bois selon la norme NDS 2018

Analyse d’une poutre en bois

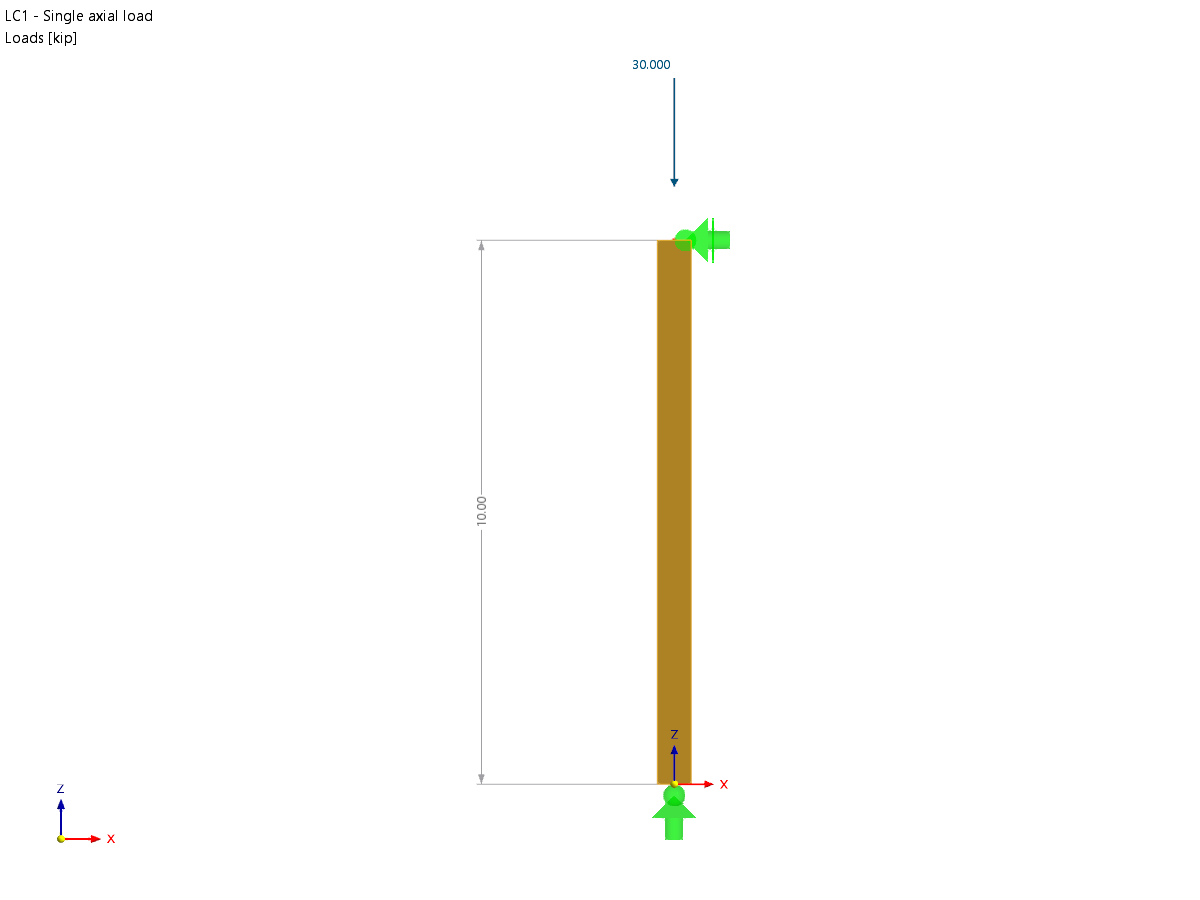
Une poutre Structural Select en sapin de Douglas et mélèze (nord) d'une longueur nominale de 4 po x 14 po avec une charge ponctuelle à mi-portée de 2 500 kip sera calculée. Le but de ce calcul est de déterminer les facteurs de flexion ajustés et la résistance en flexion de cette poutre. On suppose une durée de charge normale et des appuis articulés à chaque extrémité de barre. Les critères de charge ont été simplifiés pour cet exemple. Les critères de chargement normaux peuvent être référencés dans la clause 1.4.4 [1]. La Figure 01 montre un diagramme de poutre simple avec charges et dimensions.

1 Détails sur les charges de poutre et les dimensions

Propriétés de la poutre

La section utilisée dans cet exemple est un bois de dimension nominale de 4 po x 14 po. Les propriétés de section réelles de la poutre en bois sont calculées comme suit :

• b = 3,50 po
• d = 13,25 po
• L = 15 pi

• Aire de la section brute :
  $${\mathrm{A}}_{\mathrm{g}}= \mathrm{b} · \mathrm{d} = (3.50 \mathrm{in}) · (13.25 \mathrm{in}) = 46.38 {\mathrm{in}}^2$$

  aire de la section brute
• Module de section :
  $${\mathrm{S}}_{\mathrm{x}} = \frac{\mathrm{b} · {\mathrm{d}}^2}{6} = \frac{(3.50 \mathrm{in}) · {(13.25 \mathrm{in})}^2}{6} = 102.41 {\mathrm{in}}^3$$

  Modules de section
• Moment d’inertie :
  $${\mathrm{I}}_{\mathrm{x}} = \frac{\mathrm{b} · {\mathrm{d}}^3}{12} = \frac{(3.50 \mathrm{in}) · {(13.25 \mathrm{in})}^3}{12} = 678.48 {\mathrm{in}}^4$$

  Moment d’inertie

Le matériau utilisé pour cet exemple est « Select Structural Douglas Fir-Larch (North) » (pin Douglas et mélèze). Ses propriétés sont les suivantes :

• Valeur de calcul de référence en flexion : F_b = 1 350 psi
• Module d’élasticité minimal : E_min = 690.000 psi

Facteurs d’ajustement des poutres

Les facteurs de stabilité (ou facteurs d’ajustement) doivent être appliqués à la valeur de calcul de référence en flexion (F_b) pour calculer des barres en bois selon la norme NDS 2018 et la méthode ASD. On obtient ainsi la valeur de calcul en flexion ajustée (F'_b). Le facteur F'c est déterminé à l’aide de l'équation suivante, qui dépend fortement des facteurs d’ajustement énumérés dans le tableau 4.3.1 [1] :

Chaque facteur d’ajustement est déterminé comme suit :

C_D

Le facteur de durée de charge est implémenté pour prendre en compte différentes périodes de charge. Ce facteur permet de considérer la neige, le vent et les séismes. Ce coefficient doit être multiplié par toutes les valeurs de calcul de référence sauf pour le module d’élasticité (E), le module d’élasticité de stabilité de la poutre et du poteau (E_min) et les efforts de compression perpendiculaires au fil (F_c) selon la clause 4.3.2 [1]. C_D est dans ce cas défini sur 1,00 selon la clause 2.3.2 [1], en supposant une durée de charge normale de 10 ans.

C_M

Le facteur d’humidité de service fait référence aux valeurs de calcul pour le bois de sciage structural selon les conditions d’humidité spécifiées dans la clause 4.1.4 [1]. Dans ce cas, d’après la clause 4.3.3 [1], C_M est défini sur 1,00.

C_t

Le facteur de température est contrôlé par l’exposition permanente d’une barre à des températures élevées (jusqu'à 150 degrés Fahrenheit). Toutes les valeurs de calcul de référence sont multipliées par C_t. Selon le tableau 2.3.3 [1], C_t est défini à 1,00 pour toutes les valeurs de calcul de référence si les températures sont inférieures ou égales à 100 degrés Fahrenheit.

C_F

Le facteur de taille pour le bois de sciage prend en compte le fait que le bois n’est pas un matériau homogène. La taille de la poutre et le type de bois sont pris en compte. Pour cet exemple, notre poutre a une largeur comprise entre 2 pouces et 4 pouces et une profondeur nominale de 14 pouces. D’après le tableau 4A et selon le matériau ainsi que la taille de la poutre, un facteur de 1,00 est appliqué. Cette information se trouve dans la clause 4.3.6.1 [1].

C_i

Le facteur d’incision est utilisé pour prendre en compte le traitement de préservation du bois pour résister à une pourriture qui peut causer le développement de champignons. La plupart du temps, il s’agit d’un traitement sous pression, mais dans certains cas, le bois doit être incisé afin d’augmenter la surface de couverture chimique. Dans cet exemple, on suppose que le bois est incisé. Le tableau 4.3.8 [1] donne une vue d’ensemble des facteurs par lesquels chaque propriété de barre doit être multipliée.

_r

Le facteur répétitif de la barre est utilisé dans les cas où plusieurs barres en bois de sciage agissent de manière uniforme, ce qui entraîne une distribution uniforme des charges entre les barres. Ces barres ne peuvent pas être espacées de plus de 24 pouces du centre. Nous supposons dans cet exemple que la poutre est proche et reliée par un revêtement ou un enrobage. Dans ce cas, le facteur répétitif de la barre C_r est égal à 1,15 selon la clause 4.3.9 [1].

C_L

Le facteur de stabilité de la poutre vérifie que le flambement par torsion ou le flambement par axe faible ne se produit pas sur de longues travées non supportées latéralement. Cela fait référence à la clause 5.3.4 [1] et est calculé ci-dessous.

C_fu

Le facteur d’utilisation plane est utilisé selon si la charge d’une barre en bois est appliquée à l’axe faible ou à l’axe fort.

1. Pour cet exemple, nous allons appliquer la charge à l’axe fort, ce facteur ne sera donc pas inclus dans nos calculs.

C_T

Le facteur de rigidité de flambement est utilisé pour considérer le revêtement en contreplaqué, qui peut augmenter la résistance au flambement des membrures de treillis en compression. Pour cet exemple, nous supposerons qu'il n’y a pas de revêtement en contreplaqué, donc C_T est égal à 1,00.

Module d’élasticité ajusté

Les valeurs du module d’élasticité de référence (E et E_min) doivent également être ajustées. Le module d’élasticité ajusté (E' et E'_min) est déterminé à partir du tableau 4.3.1 [1] et le facteur d’incision C_i est égal à 0,95 d'après le tableau 4.3.8 [1].

Facteur de stabilité de la poutre (C_L)

Le facteur de stabilité de la poutre (C_L) est nécessaire pour calculer la valeur de calcul en flexion ajustée de la poutre et pour calculer le ratio de vérification en flexion. Les étapes suivantes incluent les équations et valeurs nécessaires pour trouver C_L.

La longueur efficace de cette poutre peut être calculée à l’aide de la longueur latérale sans appui (l_u), qui correspond à la longueur totale de la poutre. La longueur de barre convertie en pouces est utilisée dans l’équation de longueur efficace du tableau 3.3.3 [1].

Nous allons ensuite calculer l’élancement des barres en flexion (R_B) à l’aide de la clause 3.3.3.6 [1] avec la largeur, la profondeur et la portée efficace de la poutre.

La valeur critique de calcul du flambement des barres en flexion (F_be) est maintenant calculée en référence à la clause 3.3.3.8 [1]. Le module d’élasticité pour la stabilité de la poutre (E_min) et l’élancement en flexion (R_B) calculé précédemment sont utilisés.

Le facteur de stabilité de la poutre (C_L) peut maintenant être calculé par rapport à la section déjà utilisée comme référence ci-dessus.

Le facteur d’incision C_i est égal à 0,80 pour F_b selon le tableau 4.3.8 [1]. Tous les facteurs d’ajustement ont été déterminés à partir du tableau 4.3.1 [1]. Ainsi, la valeur de calcul en flexion ajustée (F'_b) peut être calculée.

Ratio de vérification de la poutre

Le but de cet exemple est d’obtenir le ratio de vérification de cette poutre simple. Cela déterminera si la taille de barre est adéquate sous la charge donnée, ou si elle doit être optimisée davantage. Le moment fléchissant maximal et la contrainte de flexion réelle sont nécessaires pour calculer ce ratio de vérification.

Le moment maximal autour de l’axe x (M_max) est calculé comme suit.

La contrainte réelle en flexion (f_b) est ensuite calculée en ajoutant les valeurs M_max et S obtenues au terme des calculs précédents. Nous pouvons le voir ci-dessous, avec la clause 3.3.2.1 [1].

Enfin, le ratio de vérification (η) selon la clause 3.3.1 peut alors être calculé.

Application dans RFEM

Le module additionnel RF-TIMBER AWC permet d'analyser et d'optimiser les sections selon les critères de charge et la capacité de barre d'une barre simple ou d'un ensemble de barres pour la vérification du bois selon la norme NDS 2018 dans RFEM. Cette option est disponible pour les méthodes de calcul LRFD ou ASD. Lorsque vous modélisez et calculez l'exemple de poutre ci-dessus dans RF-TIMBER AWC, les résultats peuvent être comparés.

• Visionneuse 3D | Google
• Visionneuse 3D | Babylon
• Réalité virtuelle

2 Modèle RFEM

La barre, les conditions de charge et les méthodes de calcul sont sélectionnées dans le tableau des Données de base du module additionnel RF-TIMBER AWC. Le matériau et les sections sont définis à partir de RFEM et la durée de charge est réglée sur dix ans. La condition de service d’humidité est définie sur « Sèche » et la température est inférieure ou égale à 100 degrés Fahrenheit. Le déversement est défini selon le tableau 3.3.3 [1]. Les calculs effectués par le module permettent d’obtenir une contrainte réelle en flexion (f_b) de 1 098,50 psi et une valeur de calcul en flexion ajustée (f'_b) de 1 189,59 psi. Un ratio de vérification (η) de 0,92 est déterminé à partir de ces valeurs et correspond aux calculs analytiques manuels ci-dessus.

3 Boîte de dialogue dans le module additionnel RF-TIMBER AWC