The internal forces in plates with nonlinear material result from the numerical integration of the stresses over the thickness d of the plate, as shown in Formula 1.
Please note that numerical quadrature means approximating the above integral by a weighted finite sum (Formula 2) for n points over the thickness -d/2 ≤ z1 < ... < zn ≤ d/2, and so-called weights wi, which are specific to a given quadrature and the number n.
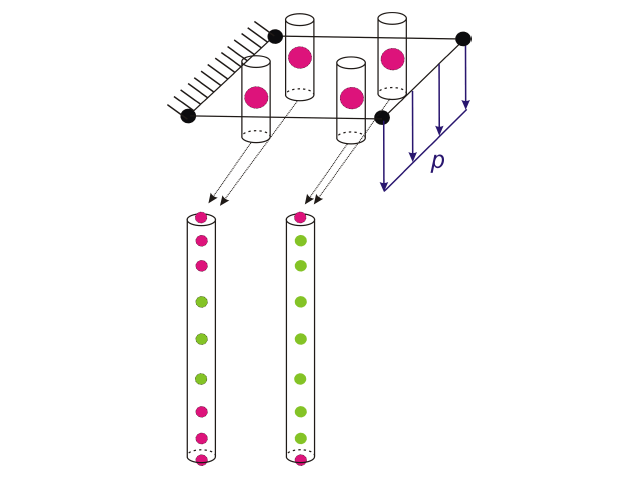
Up to RFEM version 6.02.0049 this numerical integration is performed with a 9-point Gauss-Lobatto quadrature rule containing the endpoints of the interval, i.e., the top and bottom of the thickness. This is accurate for polynomials up to order 15 (2*9-3), regardless of the material model or the user-defined diagram. Figure 1 shows the 9 nodes through the thickness for Gauss-Lobatto squaring at each planar integration point in a 2D finite element.
Hence, for materials with a "less good" stress-strain curve, the internal forces in a severely cracked slab can be approximated by the standard integration scheme with a numerical error greater than 10%. One of these materials is fiber reinforced concrete and its tensile behavior. Figure 2 shows the typical stress-strain diagram for fiber-reinforced concrete (tension on the left, compression on the right).
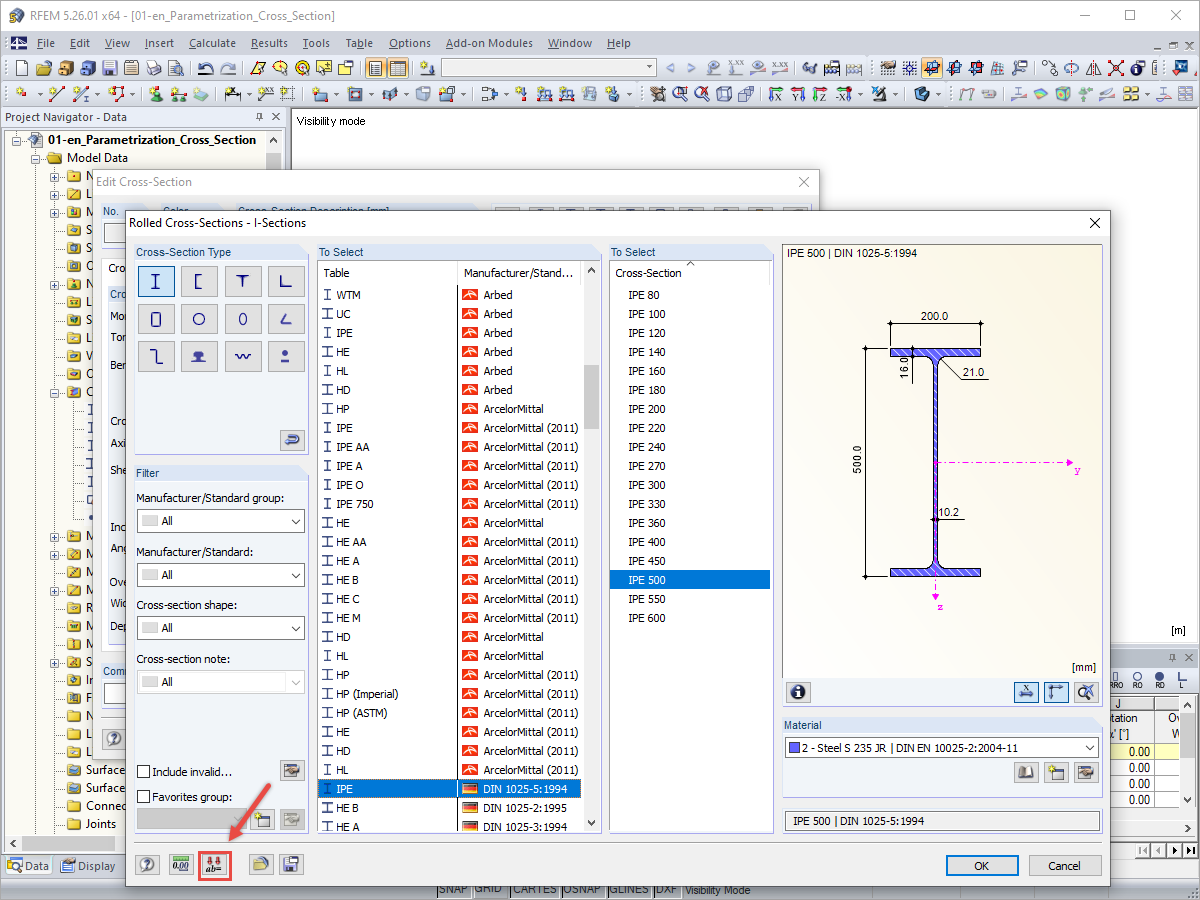
To solve this problem, a custom option is introduced in RFEM 6.02.0049 to specify the details of the numerical integration over the plate thickness (Figure 3). This option allows you as a user to change both the number of integration points (between 3 and 99) and the quadrature rule itself. Now, you can select Trapezoidal or Simpson's rule in addition to Gauss-Lobatto squaring. Note, however, that this will probably only improve integration in some very specific cases.
It is also important to know that the Gauss-Lobatto and Simpson’s rules explicitly require an odd number of integration points. So, if the user-defined number is an even number, the next largest odd number is considered for the calculation. In other words, if the user input is 4, for example, the calculation uses 5 integration points through the thickness.
An advantage of this new option is that you can improve computational performance by reducing the number of integration points in 2D structural elements with nonlinear materials. For example, you can reduce the number of integration points in regions which are not considered to be of great interest (such as regions within the elastic range).
The burning question that arises is the "right" number of integration points. Still, this is a question with no right answer. This depends on the stress-strain diagram of the material and the actual stress state of the finite elements under the given load; therefore, insight from the engineer is required in any case.
.png?mw=600&hash=49b6a289915d28aa461360f7308b092631b1446e)
