Los esfuerzos internos en placas con material no lineal resultan de la integración numérica de las tensiones sobre el espesor d de la placa, como se muestra en la fórmula 1.
Tenga en cuenta que la cuadratura numérica significa aproximar la integral anterior mediante una suma finita ponderada (fórmula 2) para n puntos sobre el espesor -d/2 ≤ z1 < ... < zn ≤ d/2, y los llamados pesos wi, que son específicos para una cuadratura dada y el número n.
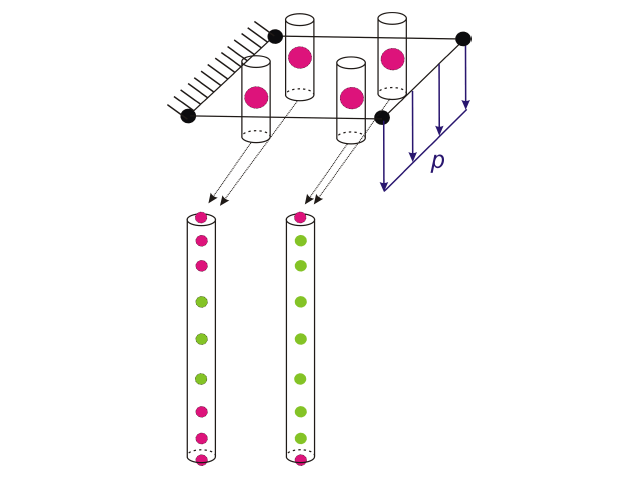
Hasta la versión de RFEM 6.02.0049, esta integración numérica se realiza con una regla de cuadratura de Gauss-Lobatto de 9 puntos que contiene los puntos finales del intervalo, es decir, la parte superior e inferior del espesor. Esto es preciso para polinomios hasta el orden 15 (2*9 - 3), independientemente del modelo de material o del diagrama definido por el usuario. La figura 01 muestra los 9 nudos a través del espesor para la cuadratura de Gauss-Lobatto en cada punto de integración plano en un elemento finito 2D.
Por lo tanto, para materiales con una curva tensión-deformación "menos buena", los esfuerzos internos en una losa severamente fisurada se pueden aproximar mediante el esquema de integración estándar con un error numérico superior al 10%. Uno de estos materiales es el hormigón reforzado con fibras y su comportamiento a tracción. La figura 02 muestra el diagrama tensión-deformación típico para hormigón reforzado con fibras (tracción a la izquierda, compresión a la derecha).
Para resolver este problema, se introduce una opción personalizada en RFEM 6.02.0049 para especificar los detalles de la integración numérica sobre el espesor de la placa (figura 3). Esta opción le permite como usuario cambiar tanto el número de puntos de integración (entre 3 y 99) como la regla de cuadratura en sí. Ahora, puede seleccionar la regla del trapecio o de Simpson además de la cuadratura de Gauss-Lobatto. Sin embargo, tenga en cuenta que esto probablemente solo mejorará la integración en algunos casos muy específicos.
También es importante saber que las reglas de Gauss-Lobatto y Simpson requieren explícitamente un número impar de puntos de integración. Por lo tanto, si el número definido por el usuario es un número par, se considera el siguiente número impar más grande para el cálculo. En otras palabras, si la entrada del usuario es 4, por ejemplo, el cálculo utiliza 5 puntos de integración a través del espesor.
Una ventaja de esta nueva opción es que puede mejorar el rendimiento computacional al reducir el número de puntos de integración en elementos estructurales 2D con materiales no lineales. Por ejemplo, puede reducir el número de puntos de integración en regiones que no se consideran de gran interés (como las regiones dentro del intervalo elástico).
La pregunta candente que surge es el número "correcto" de puntos de integración. Sobre eso todavía no hay una respuesta correcta. Esto depende del diagrama tensión-deformación del material y del estado de tensión real de los elementos finitos bajo la carga proporcionada; por tanto, se requiere una visión del ingeniero en cualquier caso.