Le forze interne nelle piastre con materiale non lineare risultano dall'integrazione numerica delle tensioni sullo spessore d della piastra, come mostrato nella Formula 1.
Si noti che quadratura numerica significa approssimare l'integrale sopra di una somma finita ponderata (Formula 2) per n punti sullo spessore -d/2 ≤ z1 < ... < zn ≤ d/2, e i cosiddetti pesi wi, che sono specifici di una data quadratura e del numero n.
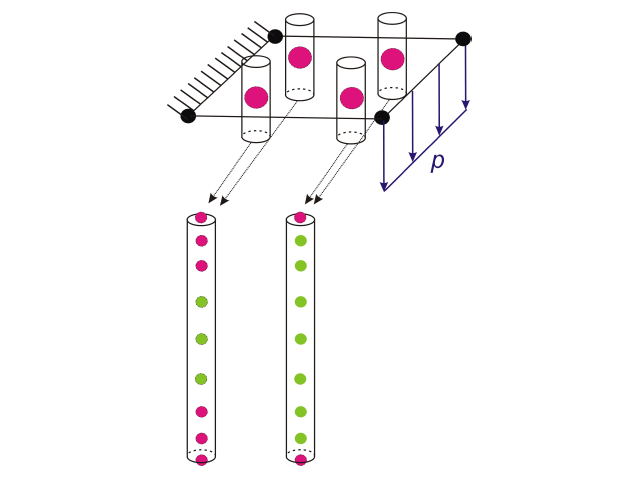
Fino a RFEM versione 6.02.0049 questa integrazione numerica viene eseguita con una regola di quadratura di Gauss-Lobatto a 9 punti contenente i punti finali dell'intervallo, ovvero la parte superiore e inferiore dello spessore. Questo è accurato per polinomi fino all'ordine 15 (2*9-3), indipendentemente dal modello del materiale o dal diagramma definito dall'utente. La Figura 1 mostra i 9 nodi attraverso lo spessore per la quadratura di Gauss-Lobatto in ogni punto di integrazione planare in un elemento finito 2D.
Quindi, per i materiali con una curva tensione-deformazione "meno buona", le forze interne in una soletta gravemente fessurata possono essere approssimate dallo schema di integrazione standard con un errore numerico maggiore del 10%. Uno di questi materiali è il calcestruzzo fibrorinforzato e il suo comportamento a trazione. La Figura 2 mostra il tipico diagramma tensione-deformazione per il calcestruzzo fibrorinforzato (trazione a sinistra, compressione a destra).
Per risolvere questo problema, in RFEM 6.02.0049 è stata introdotta un'opzione personalizzata per specificare i dettagli dell'integrazione numerica sullo spessore della piastra (Figura 3). Questa opzione consente all'utente di modificare sia il numero di punti di integrazione (tra 3 e 99) sia la regola di quadratura stessa. Ora, oltre alla quadratura di Gauss-Lobatto, puoi selezionare la regola Trapezoidale o Simpson'. Si noti, tuttavia, che questo probabilmente migliorerà l'integrazione solo in alcuni casi molto specifici.
È anche importante sapere che le regole di Gauss-Lobatto e Simpson richiedono esplicitamente un numero dispari di punti di integrazione. Quindi, se il numero definito dall'utente è un numero pari, per il calcolo viene considerato il numero dispari successivo più grande. In altre parole, se l'input dell'utente è 4, ad esempio, il calcolo utilizza 5 punti di integrazione attraverso lo spessore.
Un vantaggio di questa nuova opzione è che è possibile migliorare le prestazioni di calcolo riducendo il numero di punti di integrazione negli elementi strutturali 2D con materiali non lineari. Ad esempio, è possibile ridurre il numero di punti di integrazione nelle regioni che non sono considerate di grande interesse (come le regioni all'interno dell'intervallo elastico).
La domanda scottante che si pone è il numero "giusto" di punti di integrazione. Tuttavia, questa è una domanda senza una risposta giusta. Ciò dipende dal diagramma tensione-deformazione del materiale e dallo stato tensionale effettivo degli elementi finiti sotto il carico dato; pertanto, è comunque necessaria l'intuizione dell'ingegnere.