Les efforts internes dans les plaques avec un matériau non linéaire résultent de l'intégration numérique des contraintes sur l'épaisseur d de la plaque, comme le montre la formule 1.
Veuillez noter que la quadrature numérique correspond à une approximation de l'intégrale ci-dessus par une somme finie pondérée (formule 2) pour n points sur l'épaisseur -d/2 ≤ z1 < ... < zn ≤ d/2, et les poids wi, qui sont spécifiques à une quadrature donnée et au nombre n.
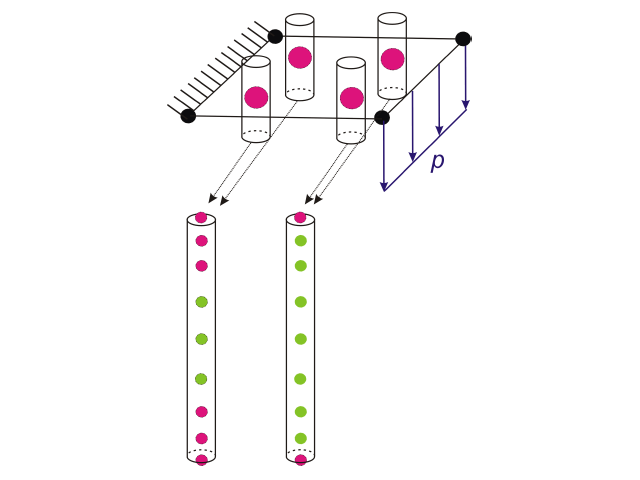
Jusqu’à la version 6.02.0049 de RFEM, cette intégration numérique est effectuée à l’aide d'une règle de quadrature de Gauss-Lobatto à 9 points contenant les extrémités de l’intervalle, c’est-à-dire le haut et le bas de l’épaisseur. Ceci est précis pour les polynômes jusqu'à l'ordre 15 (2*9-3), quel que soit le modèle de matériau ou le diagramme défini par l'utilisateur. La Figure 1 montre les 9 nœuds à travers l'épaisseur pour la quadrature de Gauss-Lobatto à chaque point d'intégration planaire dans un élément fini 2D.
Ainsi, pour les matériaux avec une courbe contrainte-déformation « moins bonne », les efforts internes dans une dalle fortement fissurée peuvent être approximés par le schéma d'intégration standard avec une erreur numérique supérieure à 10 %. L’un de ces matériaux est le béton fibré et son comportement en traction. La Figure 2 montre le diagramme contrainte-déformation type du béton fibré (traction à gauche, compression à droite).
Pour résoudre ce problème, une option personnalisée est introduite dans RFEM 6.02.0049 pour spécifier les détails de l'intégration numérique sur l'épaisseur de plaque (Figure 3). Cette option vous permet, en tant qu'utilisateur, de modifier à la fois le nombre de points d'intégration (entre 3 et 99) et la règle de quadrature elle-même. Vous pouvez maintenant sélectionner une règle trapézoïdale ou une règle de Simpson en plus de la quadrature de Gauss-Lobatto. Notez cependant que cela n'améliorera probablement l'intégration que dans certains cas très spécifiques.
Il est également important de savoir que les règles de Gauss-Lobatto et de Simpson nécessitent explicitement un nombre impair de points d'intégration. Ainsi, si le nombre défini par l'utilisateur est un nombre pair, le plus grand nombre impair suivant est considéré pour le calcul. En d'autres termes, si l'entrée utilisateur est 4, par exemple, le calcul utilise 5 points d'intégration à travers l'épaisseur.
L'un des avantages de cette nouvelle option est qu'elle permet d'améliorer les performances de calcul en réduisant le nombre de points d'intégration dans les éléments de structure 2D avec des matériaux non linéaires. Par exemple, vous pouvez réduire le nombre de points d’intégration dans les régions qui ne sont pas considérées comme présentant un grand intérêt (telles que les régions situées dans le domaine élastique).
La question cruciale qui se pose est celle du « bon » nombre de points d'intégration. Il s'agit néanmoins d'une question sans bonne réponse. Cela dépend du diagramme contrainte-déformation du matériau et de l'état de contrainte réel des éléments finis sous la charge donnée ; l'avis de l'ingénieur est donc nécessaire dans tous les cas.