Os esforços internos em placas de material não linear resultam da integração numérica das tensões sobre a espessura d da placa, como apresentado na Fórmula 1.
Observe que quadratura numérica significa aproximar o integral acima por uma soma finita ponderada (Fórmula 2) para n pontos sobre a espessura -d/2 ≤ z1 < ... < zn ≤ d/2, e os chamados pesos wi, que são específicos de uma quadratura dada e do número n.
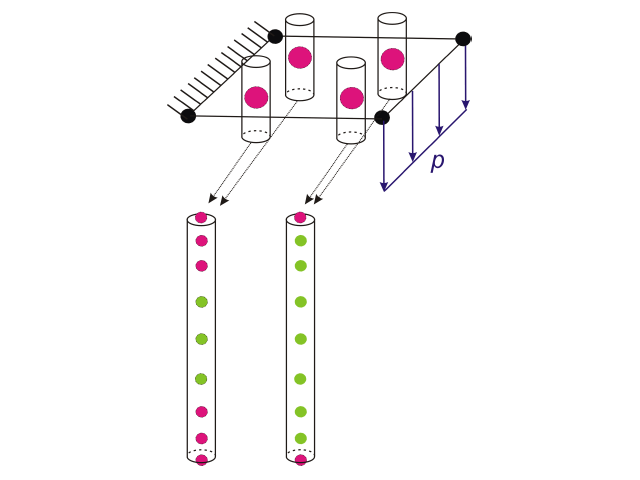
Até à versão 6.02.0049 do RFEM esta integração numérica era realizada com uma regra de quadratura de Gauss-Lobatto de 9 pontos contendo as extremidades do intervalo, ou seja, as partes superior e inferior da espessura. Isto é preciso para polinômios até a ordem 15 (2*9-3), independentemente do modelo do material ou do diagrama definido pelo utilizador. A Figura 1 mostra os 9 nós através da espessura para a quadratura de Gauss-Lobatto em cada ponto de integração plana num elemento finito 2D.
Assim, para materiais com uma curva de tensão-deformação "menos boa", os esforços internos numa laje muito fendilhado podem ser aproximados pelo esquema de integração padrão com um erro numérico superior a 10%. Um desses materiais é o betão armado com fibras e o seu comportamento à tração. A Figura 2 apresenta um diagrama tensão-deformação típico para betão armado com fibras (tração à esquerda, compressão à direita).
Para solucionar este problema, é introduzida no RFEM 6.02.0049 uma opção personalizada para especificar os detalhes da integração numérica sobre a espessura da placa (Figura 3). Esta opção permite ao utilizador alterar tanto o número de pontos de integração (entre 3 e 99) como a própria regra de quadratura. Agora pode selecionar a regra Trapezoidal ou de Simpson' além da quadratura de Gauss-Lobatto. Observe, no entanto, que isso provavelmente só melhorará a integração em alguns casos muito específicos.
Também é importante saber que as regras de Gauss-Lobatto e de Simpson requerem explicitamente um número ímpar de pontos de integração. Assim sendo, se o número definido pelo utilizador for um número par, o segundo maior número ímpar é considerado para o cálculo. Por outras palavras, se a entrada do utilizador for 4, por exemplo, o cálculo utiliza 5 pontos de integração através da espessura.
Uma vantagem desta nova opção é que pode melhorar o desempenho computacional reduzindo o número de pontos de integração em elementos estruturais 2D com materiais não lineares. Por exemplo, é possível reduzir o número de pontos de integração em regiões que não são consideradas de grande interesse (tais como regiões do intervalo elástico).
A questão candente que se coloca é o número "certo" de pontos de integração. Ainda assim, esta é uma pergunta sem resposta certa. Isto depende do diagrama tensão-deformação do material e do estado de tensão real dos elementos finitos para um determinado carregamento; portanto, é necessária uma visão geral do engenheiro em qualquer caso.