5071x

18.12.2020

Phénomène de déversement dans les structures bois | Exemple 2

L'article précédent, Phénomènes de déversement dans les structures bois | Exemple 1, explique l'application pratique de la détermination du moment fléchissant critique Mcrit ou de la contrainte de flexion critique σcrit pour le flambement latéral d'une poutre en flexion à l'aide d'exemples simples. Dans cet article, le moment fléchissant critique est déterminé en considérant une fondation élastique résultant d'un contreventement.

Modèle de calcul de structure

Les treillis doivent être analysés pour le flambement latéral dans le cas du système représenté sur la Figure 01. Dans le plan de toiture, se trouvent six barres de treillis sous forme de poutres parallèles de 18 m de longueur et deux contreventements. Les poutres des côtés du pignon sont supportées par des poteaux et ne sont pas considérées pour le calcul. Une charge de calcul q_d de 10 kN/m agit sur les barres en treillis.

Modèle de structure

Données du modèle

L	18	m	Longueur de la poutre
b	120	mm	Largeur de la poutre
h	1.200	mm	Hauteur de la poutre
GL24h			Matériau selon l'EN 14080
I_z	172.800.000	mm⁴	Moment d'inertie
I_T	647.654.753	mm⁴	Inertie de torsion
q_d	10	kN/m	Charge de calcul
a_z	600	mm	Position de la charge
e	600	mm	Position de la fondation

Remarque : Même si les équations suivantes pour E et G ne se réfèrent pas explicitement aux valeurs de quantiles à 5 % dans l'index, elles ont été prises en compte en conséquence.

Poutre à travée simple avec maintien latéral et en torsion sans appuis intermédiaires

Poutre à travée simple avec maintien latéral et de torsion sans appuis intermédiaires

Par souci d'exhaustivité, la barre en treillis est d'abord analysée, sans appuis latéraux (voir la Figure 02). La longueur de barre équivalente résulte de l'application de charge sur la face supérieure du treillis avec a₁ = 1,13 et a₂ = 1,44 comme suit :

l_{ef} = \frac{L}{a_{1} \cdot (1 - a_{2} \cdot \frac{a_{z}}{L} \cdot \sqrt{\frac{E_{0, 05} \cdot I_{Z}}{G_{0, 05} \cdot I_{T}}})}

l_ef	longueur de barre équivalente
L	Longueur de poutre, espacement entre les appuis latéraux
un₁ , un₂	Facteurs utilisés pour le déversement latéral
a_z	distance d'application de la charge au centre de cisaillement
E_0,05	5 % Quantile des Elastizitätsmoduls
G_0,05	5 % Quantile des Schubmoduls
I_z	module d'inertie selon l'axe faible
I_T	Inertie de torsion

longueur de barre équivalente

l_ef = 17,79 m

Le moment fléchissant critique peut alors être calculé comme suit :

M_{crit} = \frac{π \cdot \sqrt{E_{0, 05} \cdot I_{Z} \cdot G_{0, 05} \cdot I_{tor}}}{l_{ef}}

M_crit	Moment fléchissant critique
E_0,05	5 % Quantile des Elastizitätsmoduls
G_0,05	5 % Quantile des Schubmoduls
I_z	module d'inertie selon l'axe faible
I_T	Inertie de torsion
l_ef	longueur de barre équivalente

Moment de flexion critique

M_crit = 134,52 kNm

Ces exemples n'augmentent pas le produit des propriétés de rigidité à 5 % en raison de l'homogénéisation des poutres en bois lamellé-collé.

Le moment fléchissant agissant sur les treillis est le suivant :

M_{d} = \frac{q_{d} \cdot L^{2}}{8}

M_d	Moment de calcul
q_d	charge de calcul
L	Longueur de la poutre

Moment de calcul

M_d = 405,00 kNm

L'analyse des valeurs propres avec le module additionnel RF-/FE-LTB fournit un facteur de charge critique de flambement de 0,3334. On obtient ainsi le moment fléchissant critique

M_crit = 0,3334 ⋅ 405 kNm = 135,03 kNm

qui est donc identique au résultat de la solution analytique.

Ergebnis der Eigenwertanalyse für den gabelgelagerter Einfeldträger ohne Zwischenabstützungen

Comme prévu pour cette barre en treillis élancée non supportée, le moment fléchissant agissant est supérieur (par un facteur 3) au moment fléchissant critique et le treillis n'est donc pas suffisamment maintenu contre le flambement latéral. Cependant, un contreventement devrait agir contre cela, ce qui est désormais considéré pour le calcul.

Poutre à travée simple avec maintien latéral et en traction et appuis intermédiaires rigides

Poutre à travée simple avec maintien latéral et de torsion avec appuis intermédiaires rigides

Si le contreventement est assez rigide, l'espacement entre les appuis latéraux (par exemple, par des pannes) est souvent utilisé comme longueur de barre équivalente pour l'analyse du déversement latéral. Cette procédure a été décrite dans l'article précédent Phénomène de déversement dans les structures bois | Exemples 1. Ainsi, 2,25 m sont utilisés comme L. Pour a₁ = 1,00 et a₂ = 0,00 :

l_{ef} = \frac{L}{a_{1} \cdot (1 - a_{2} \cdot \frac{a_{z}}{L} \cdot \sqrt{\frac{E_{0, 05} \cdot I_{z}}{G_{0, 05} \cdot I_{T}}})}

l_ef	Longueur de barre équivalente
L	Longueur de poutre, espacement entre les appuis latéraux
un₁ , un₂	Facteurs utilisés pour le déversement latéral
a_z	distance d'application de la charge au centre de cisaillement
E_0,05	5 % du module d'élasticité
G_0,05	5 % du module de cisaillement
I_z	module d'inertie selon l'axe faible
I_T	Inertie de torsion

longueur de barre équivalente

l_ef = 2,25 m

Résultats suivants pour le moment fléchissant critique :

M_{crit} = \frac{π \cdot \sqrt{E_{0, 05} \cdot I_{Z} \cdot G_{0, 05} \cdot I_{tor}}}{l_{ef}}

M_crit	Moment fléchissant critique
E_0,05	5 % Quantile des Elastizitätsmoduls
G_0,05	5 % Quantile des Schubmoduls
I_z	module d'inertie selon l'axe faible
I_T	Inertie de torsion
l_ef	longueur de barre équivalente

Moment de flexion critique

M_crit = 1 063,51 kNm

Étant donné que le moment fléchissant agissant sur la poutre est inférieur au moment fléchissant critique, la poutre n'est pas menacée par un flambement latéral en cas d'appuis intermédiaires rigides.

L'analyse des valeurs propres avec le module additionnel RF-/FE-LTB fournit un facteur de charge critique de flambement de 2,7815. On obtient ainsi le moment fléchissant critique

M_{crit} = η \cdot M_{d}

M_crit	Moment fléchissant critique
η	facteur de charge de flambement
M_d	Moment de calcul

Moment de flexion critique

M_crit = 2,7815 ⋅ 405 kNm = 1 126,50 kNm

Ergebnis der Eigenwertanalyse für den gabelgelagerten Einfeldträger mit starren Zwischenabstützungen

Poutre à travée simple avec maintien latéral et en torsion et fondation élastique de barre

Poutre à travée simple avec maintien latéral et de torsion et fondation élastique de barre

Comme décrit dans Phénomène de déversement dans les structures bois | Principes théoriques , la longueur de barre équivalente pour les barres sur fondation élastique est complétée par les facteurs α et β dans [1]. Il est ainsi possible de considérer la rigidité de cisaillement d'un contreventement pour le flambement latéral des treillis. La rigidité de cisaillement du contreventement peut être déterminée par exemple selon la Figure 6.34 de [2]. Comme indiqué ci-dessus, cela dépend du type de contreventement, de la rigidité des diagonales et des poteaux, de l'inclinaison des diagonales et de la ductilité des organes d'assemblage. Pour le contreventement représenté sur la Figure 01, on obtient la rigidité de cisaillement suivante :

s_{id} = E_{D} \cdot A_{D} \cdot \sin (^{α) 2} \cdot \cos (α)

s_id	Rigidité de cisaillement idéale des contreventements
E_d	5 % Quantile des Elastizitätsmoduls der Diagonalen
A_d	Aire de section des diagonales
α	Angle entre les diagonales et les membrures

Rigidité de cisaillement idéale pour les contreventements

E_D est le module d'élasticité des diagonales et A_D de leur aire de section. Cependant, l'équation ci-dessus n'inclut pas la ductilité des organes d'assemblage des diagonales. Celles-ci et l'allongement de barre des diagonales peuvent être considérés à l'aide de l'aire de section fictive A_D'. Le calcul est effectué comme suit :

s_{id} = E_{D} \cdot A_{D}' \cdot \sin (^{α) 2} \cdot \cos (α)

s_id	Rigidité de cisaillement idéale des contreventements
E_d	5 % Quantile des Elastizitätsmoduls der Diagonalen
A_d'	Aire notionnelle des diagonales
α	Angle entre les diagonales et les membrures

Rigidité de cisaillement idéale pour les contreventements

où

A_{D}' = \frac{A_{D}}{1 + \frac{E_{D} \cdot A_{D}}{L_{D}} \cdot \sum \frac{1}{K_{ser}}}

A_d'	Aire notionnelle des diagonales
A_d	Aire de section des diagonales
E_d	5 % Quantile des Elastizitätsmoduls der Diagonalen
L_d	Longueur des diagonales
K_ser	Module de glissement de la connexion

Aire de section théorique des diagonales

Les diagonales ont une dimension l/h de 120/200 mm et une longueur L_D de 4,59 m. Le module de glissement de l’assemblage de chaque côté des diagonales doit être de 110 000 N/mm.

La zone idéale est donc

A_D' = 12 548 mm²

la rigidité de cisaillement d'un contreventement avec un angle d'inclinaison de la membrure de 60,64 ° est

s_{id} = E_{D} \cdot A_{D}' \cdot \sin (^{α) 2} \cdot \cos (α)

s_id	Rigidité de cisaillement idéale des contreventements
E_d	5 % Quantile des Elastizitätsmoduls der Diagonalen
A_d'	Aire notionnelle des diagonales
α	Angle entre les diagonales et les membrures

Rigidité de cisaillement idéale pour les contreventements

s_id = 44,864 kN

La fondation de barre par contreventement peut être convertie selon la Formule 7.291 de [2] comme suit :

K_{y}' = s_{id} \cdot \frac{π^{2}}{L^{2}}

K_{y}' = 44.864 kN \cdot \frac{π^{2}}{(^{18 m) 2}} = 1.367 \frac{kN}{m^{2}} = 1, 367 \frac{N}{{mm}^{2}}

K_y'	Fondation de barre élastique par contreventement
s_id	Rigidité de cisaillement idéale des contreventements
L	Longueur du contreventement

Fondation de barre élastique par contreventement

Pour deux contreventements et six treillis, la constante de ressort suivante est disponible par treillis :

K_{y} = \frac{2 \cdot K_{y}'}{6}

K_y	Fondation de barre élastique par barre de treillis
K_y'	Fondation de barre élastique par contreventement

Fondation de barre élastique par barre de treillis

K_y = 455,6 kN/m² = 0,456 N/mm²

Si K_G = ∞, K_θ = 0, K_y = 0,456 N/mm², e = 600 mm, a₁ = 1,13 et a₂ = 1,44, la longueur de barre équivalente est obtenue comme suit :

l_{ef} = \frac{L}{a_{1} \cdot (1 - a_{2} \cdot \frac{a_{z}}{L} \cdot \sqrt{\frac{E_{0, 05} \cdot I_{z}}{G_{0, 05} \cdot I_{T}}})} \cdot \frac{1}{α \cdot β}

l_ef	longueur de barre équivalente
L	Longueur de poutre, espacement entre les appuis latéraux
un₁ , un₂	Facteurs utilisés pour le déversement latéral
a_z	distance d'application de la charge au centre de cisaillement
E_0,05	5 % Quantile des Elastizitätsmoduls
G_0,05	5 % Quantile des Schubmoduls
I_z	module d'inertie selon l'axe faible
I_T	Inertie de torsion
α, β	Facteurs pour considérer une fondation membre

longueur de barre équivalente

l_ef = 0,13

Le moment fléchissant critique est ainsi obtenu avec une valeur irréaliste de :

M_{crit} = \frac{π \cdot \sqrt{E_{0, 05} \cdot I_{Z} \cdot G_{0, 05} \cdot I_{tor}}}{l_{ef}}

M_crit	Moment fléchissant critique
E_0,05	5 % Quantile des Elastizitätsmoduls
G_0,05	5 % Quantile des Schubmoduls
I_z	module d'inertie selon l'axe faible
I_T	Inertie de torsion
l_ef	longueur de barre équivalente

Moment de flexion critique

M_crit = 18 482,84 kNm

Une valeur similaire à celle du système avec des appuis intermédiaires rigides est souhaitée. Comme décrit dans Déversement dans les structures bois | Théorie, l'application de la formule étendue avec α et β est limitée dans son application. Elle n'est valide qu'en cas de flèche dans une grande courbure sinusoïdale. En d'autres termes, si la fondation est très molle. Cette opération n'est plus effectuée dans cet exemple. Les fonctions propres à plusieurs ondes, qui entraînent une faible charge critique de flambement pour une constante de ressort plus importante, ne sont pas incluses dans l'équation ci-dessus, car elle est basée sur des approches de sinus monomial.

Comme vous pouvez le voir sur la Figure 07, un mode propre multi-onde est obtenu à partir de l'analyse des valeurs propres.

Ergebnis der Eigenwertanalyse für den gabelgelagerten Einfeldträger mit elastischer Stabbettung

Dans ce cas, la méthode définie par le professeur Heinrich Kreuzinger (2020) peut être appliquée. Le moment fléchissant critique est calculé comme suit :

M_{crit} = \frac{(2 \cdot e \cdot c^{*} - a_{z}^{*} \cdot B^{*}) + \sqrt{(^{2 \cdot e \cdot c^{*} - a_{z}^{*} \cdot B^{*}) 2} + 4 \cdot 1, 0 \cdot (B^{*} \cdot T^{*} - e^{*} \cdot {c^{*}}^{2})}}{2}

c^{*} = K_{y} \cdot \frac{L^{2}}{π^{2} \cdot n^{2}}

a_{z}^{*} = \frac{a_{z}}{n^{2}}

B^{*} = E_{0, 05} \cdot I_{Z} \cdot \frac{π^{2} \cdot n^{2}}{L^{2}} + c^{*}

T^{*} = G_{0, 05} \cdot I_{T} + c^{*} \cdot e^{2}

n = 1, 2, 3 . . .

M_crit	Moment fléchissant critique
a_z	distance d'application de la charge au centre de cisaillement
e	distance entre la fondation élastique de barre et le centre de cisaillement
K_y	Fondation de barre élastique par barre de treillis
L	Longueur de la poutre
n	n ^th eigensolution
E_0,05	5 % Quantile des Elastizitätsmoduls
I_z	module d'inertie selon l'axe faible
G_0,05	5 %-Quantile des Schubmoduls
I_T	Inertie de torsion

Moment de flexion critique

La constante n indique la 1re, 2e, 3e ...solution propre. Plusieurs solutions propres doivent être analysées et le moment fléchissant critique le plus faible s'applique alors. Les moments fléchissants critiques suivants sont les résultats pour n = 1...30.

n	M_crit [kNm]	n	M_crit [kNm]
1	9.523,25	16	2.214,63
2	4.281,26	17	2.339,17
3	2.294,32	18	2.464,92
4	1.605,56	19	2.591,63
5	1.354,68	20	2.719,14
6	1.282,70	21	2.847,30
7	1.294,12	22	2.976,00
8	1.348,81	23	3.105,16
9	1.428,05	24	3.234,71
10	1.522,29	25	3.364,60
11	1.626,24	26	3.494,77
12	1.736,77	27	3.625,20
13	1.851,94	28	3.755,84
14	1.970,50	29	3.886,67
15	2.091,60	30	4.017,68

M_crit devient minimal pour n = 6, et est d'environ 1 282,70 kNm.

La solution des valeurs propres du module additionnel RF-/FE-LTB (voir la Figure 07) est calculée comme suit :

M_crit = 3,4376 ⋅ 405 kNm = 1 397,25 kNm

Les deux résultats correspondent très bien. La solution analytique reste toutefois sûre, car cette méthode est basée sur une distribution constante des moments fléchissants. Une charge critique q_crit est ensuite assignée au moment fléchissant critique constant M_crit.

q_{crit} = \frac{M_{crit} \cdot 8}{L^{2}}

q_crit	Charge critique
M_crit	Moment fléchissant critique
L	Longueur de la poutre

Charge critique

Étant donné que la fondation de barre dans cet exemple est considérée comme très rigide et uniformément répartie sur la longueur de la barre en treillis, des moments de flexion critiques légèrement plus élevés que ceux des appuis simples rigides ont lieu.

Selon le chapitre 9.2.5.3 (2) de [3], les raidisseurs doivent être suffisamment rigides pour ne pas dépasser la flèche horizontale de L/500. Le calcul doit être effectué avec les valeurs de calcul des rigidités (voir [1], Chapitres NCI à 9.2.5.3).

Pour k_crit = 0,195, H = 5 m et q_p = 0,65 kN/m² comme pression dynamique de rafale, on obtient les charges suivantes (voir le Chapitre 9.2.5.3 de [3] ) :

N_{d} = (1 - k_{crit}) \cdot \frac{M_{d}}{h}

N_d	Force de stabilisation de la membrure comprimée
k_crit	Facteur de stabilité latérale
M_d	Moment de calcul
h	Hauteur de la poutre

Force de stabilisation de la membrure en compression

N_d = (1 - 0,195) ⋅ 405/1,2 = 271,68 kN

q_{d} = \sqrt{\frac{15}{L}} \cdot \frac{n \cdot N_{d}}{k_{f, 3} \cdot L}

q_d	Charge raidissante
n	Nombre de barres de treillis
L	Longueur de la poutre
k_{f, 3}	Facteur de modification pour la résistance au raidissement

Charge raidissante

q_d = 2,76 kN/m

q_{d, Wind} = γ_{Q} \cdot (c_{pe, D} \cdot c_{pe, E}) \cdot q_{p} \cdot \frac{H}{2}

q_{d, vent}	Charge de calcul due au vent
γ_Q	Coefficient partiel de sécurité pour une action variable
c_pe	Coefficient de pression externe
q_P	pression dynamique extrême
h	Hauteur du bâtiment

Charge de calcul due au vent

q_d,vent = 1,5 ⋅ (0,7 + 0,3) ⋅ 0,65 ⋅ 5/2 = 2,44 kN/m

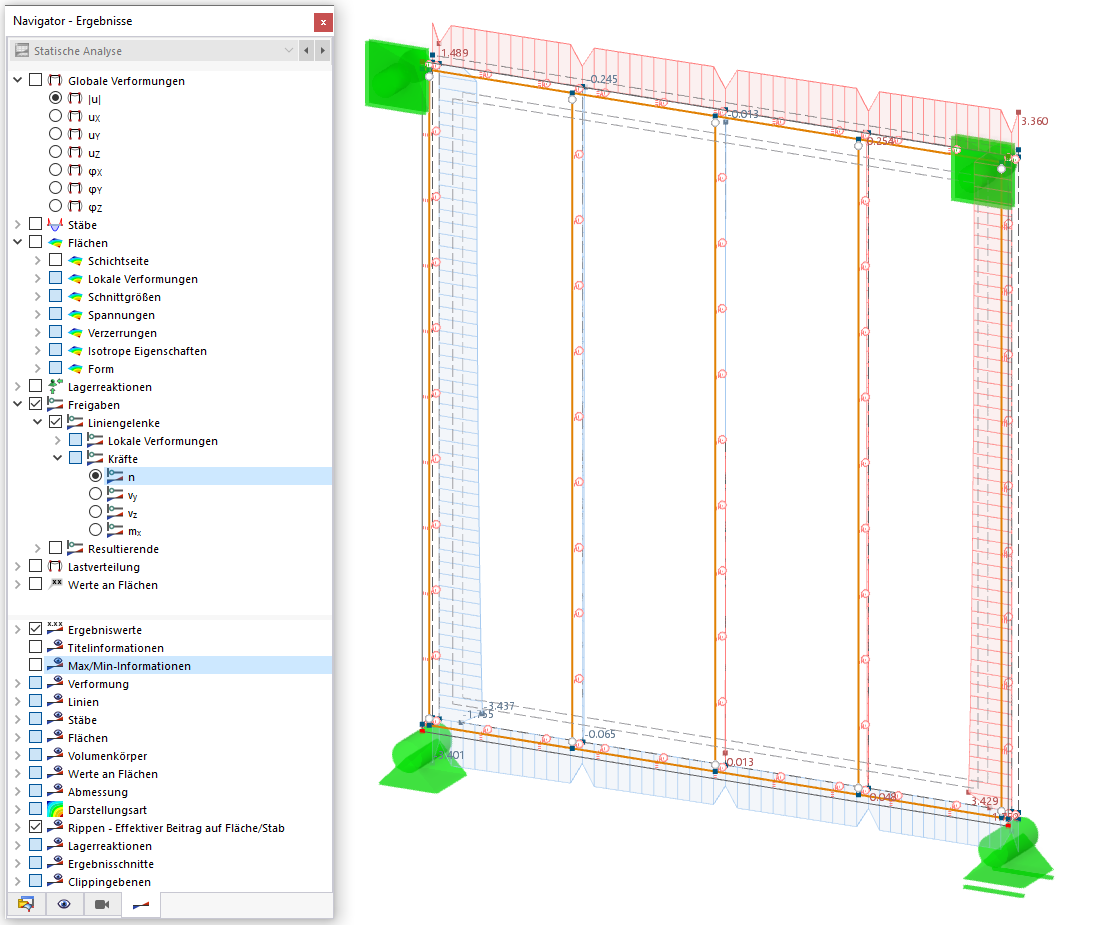
La déformation du contreventement est illustrée dans la Figure 08. Les charges ont été réduites par moitié car il y a deux contreventements.

Déplacement horizontal du contreventement de raidissement

La déformation admissible est :

\frac{L}{500} = \frac{18 m}{500} = 36, 00 mm \geq 4, 74 mm

Déformation admissible

Le résultat confirme l'hypothèse d'un contreventement très rigide et est cohérent avec les moments fléchissants critiques presque identiques du système avec des appuis intermédiaires rigides et un avec fondation élastique de barre.

Résumé

Il a été montré quelles possibilités dans la construction bois peuvent être utilisées pour analyser le déversement latéral des poutres en flexion. Pour les méthodes courantes, il est important de s'assurer que les raidisseurs sont suffisamment rigides pour supporter des appuis rigides. Des options ont été présentées dans cet article pour les cas où cette hypothèse ne s'applique pas. Les poutres en flexion et les raidisseurs doivent être calculés pour leur capacité portante et leur ELS selon la norme correspondante. Cela n'est cependant pas détaillé dans cet article.

Base de connaissance

KB 001669 | Phénomène de déversement dans les structures bois | Exemple 2

Auteur

M. Rehm est responsable du développement de produits pour les structures en bois et il fournit une assistance technique aux clients.

Liens

Références

Annexe Nationale - Eurocode 5 : Bemessung und Konstruktion von Holzbauten - Teil 1-1: Allgemeines - Allgemeine Regeln und Regeln für den Hochbau; DIN EN 1995-1-1/NA:2013-08
Petersen, C.: Statik und Stabilität der Baukonstruktionen, 2. Auflage. Wiesbaden: Vieweg, 1982
Eurocode 5 : calcul des structures en bois - Partie 1-1 : Général – Règles courantes et règles pour les bâtiments ; DIN EN 1995-1-1:2010-12

Avez-vous des questions ?

Evénements

21.05.2024

Vérification des bâtiments en CLT dans RFEM 6 selon la CSA O86:19

Webinaire

Vérification des bâtiments en CLT dans RFEM 6 selon la CSA O86:19 (États-Unis)

29.05.2024

Vérification de planchers bois dans RFEM 6

Webinaire

Vérification de planchers bois dans RFEM 6

20.11.2024

Formation en ligne

RFEM6 | Étudiants | Introduction à la vérification du bois

Vidéos

Base de connaissance

KB 001669 | Phénomène de déversement dans les structures bois | Exemple 2

Longueur: 00:02:15 min

RFEM 6 pour les étudiants | Introduction à la vérification du bois

Événement

RFEM 6 pour les étudiants | Introduction à la vérification du bois | 30 avril 2024

Longueur: 01:08:02 min

faq 005511 | Que font chaque option dans la section « Calcul de la torsion » sous l'onglet Résistance...

Foire aux questions (FAQ)

faq 005511 | Que font chaque option dans la section « Calcul de la torsion » sous l'onglet Résistance...

Longueur: 00:00:16 min

Foire aux questions (FAQ)

FAQ 005494 | Comment modéliser une poutre en bois avec des raidisseurs des deux côtés ? (éclisse)

Longueur: 00:01:22 min

Fonctionnalité de produit

Vérification de la résistance au feu des surfaces selon l'EN 1995, la SIA 265, la NDS et la CSA O86

Longueur: 00:00:56 min

Événement

Webinaire | Calculs des planchers bois dans RFEM 6

Longueur: 00:55:27 min

Événement

RFEM 6 pour les étudiants | Introduction à la vérification du bois | 29 novembre 2023

Longueur: 01:10:03 min

Fonctionnalité de produit

Optimisation des sections

Longueur: 00:00:56 min

Événement

Matinale de Dlubal Software | Paramétrage des articulations linéiques pour les panneaux CLT

Longueur: 00:47:05 min

Playlist

Modèles à télécharger

Poutre fourchue à travée simple sans maintiens latéraux intermédiaires

1981x

53x

Poutre en bois à travée simple avec appuis articulés

3229x

115x

Treillis en bois

102x

Station de charge Charges améliorées, Danemark

Modèle 000000 | Bâtiment à ossature bois

552x

114x

Bâtiment à ossature bois

447x

63x

Bâtiment en CLT

271x

27x

Plancher bois

Modèle 004717 | Plafond avec des libérations linéiques

312x

32x

Plafond avec des libérations linéiques

Modèle 004707 | Bâtiment des bureaux des Services des municipalités Communes de Kirchheim sub T modèle

326x

Bâtiment administratif avec structure en bois et éléments en béton armé

555x

Capannone industriale à Legno Siegrist Igor Carmenteria

Articles de la base de connaissance

Poutre à travée simple avec appuis articulés et sans appui intermédiaire

L'article technique « Phénomène de déversement dans les structures bois : principes théoriques » présente les principes théoriques pour la détermination analytique du moment de flexion critique M_crit ou de la contrainte de flexion critique σ_crit pour le flambement latéral d'une poutre en flexion. Dans ce nouvel article technique, plusieurs exemples sont utilisés pour vérifier la méthode analytique à l'aide du résultat de l'analyse des valeurs propres.

Lire la suite

Flambement latéral d'une poutre à travée simple

Les poutres droites élancées ayant un rapport h/b élevé présentent des risques de problèmes de stabilité lorsqu’elles sont chargées parallèlement à l'axe faible. Cela est lié au déplacement hors-plan de la semelle comprimée.

Lire la suite

Lire la suite

Ko 001848 | Vérification des poteaux en bois selon la norme NDS 2018 dans RFEM 6

Le module complémentaire Timber Design permet de calculer des poteaux en bois selon la méthode ASD de la norme NDS 2018. La précision du calcul de la résistance en compression et des facteurs d’ajustement des barres en bois est importante pour la sécurité et le calcul des composants. Cet article permet de vérifier la résistance critique maximale au flambement calculée par le module complémentaire Calcul du bois à l'aide d'équations analytiques étape par étape selon la norme NDS 2018, y compris les facteurs d'ajustement en compression, la valeur de calcul en compression ajustée et le rapport de calcul final.

Lire la suite

Captures d'écran

Modèle de structure

Poutre à travée simple avec maintien latéral et de torsion sans appuis intermédiaires

Ergebnis der Eigenwertanalyse für den gabelgelagerter Einfeldträger ohne Zwischenabstützungen

Poutre à travée simple avec maintien latéral et de torsion avec appuis intermédiaires rigides

Ergebnis der Eigenwertanalyse für den gabelgelagerten Einfeldträger mit starren Zwischenabstützungen

Poutre à travée simple avec maintien latéral et de torsion et fondation élastique de barre

Ergebnis der Eigenwertanalyse für den gabelgelagerten Einfeldträger mit elastischer Stabbettung

Déplacement horizontal du contreventement de raidissement

Modèle de la meilleure charge d'énergie dans RWIND

Fonctionnalités de produit

Fonctionnalité 002792 | Élément de panneau en bois

Avec le type d'épaisseur « Panneau de poutre », vous pouvez modéliser des ossatures bois en 3D. Il suffit de définir la géométrie de la surface et les éléments du panneau en bois sont générés via une structure barre-surface interne, y compris la simulation de la flexibilité de l'assemblage.

Accéder à la vidéo explicative

Lire la suite

Fonctionnalité 002585 | Vérification de la résistance au feu des surfaces pour l'EN 1995 et la SIA 265

Vous avez la possibilité d'effectuer une vérification de la résistance au feu des surfaces à l'aide de la méthode de la section réduite. La réduction est appliquée sur l'épaisseur de la surface. Les vérifications peuvent être effectuées pour tous les matériaux bois admis pour le calcul.

Pour le bois lamellé-croisé, vous pouvez choisir entre les différents types d'adhésif, et décider la chute de parties de couche carbonisée est possible de sorte qu'une carbonisation accrue soit attendue dans certaines zones de couche.

Lire la suite

Fonctionnalité 002615 | Superstructures en bois lamellé-croisé pour les États-Unis, le Canada et la Suisse

Entre autres, les fabricants de bois lamellé-croisé suivants sont disponibles dans la bibliothèque de structures en couches :

Binderholz (USA)
KLH (USA, CAN)
Kalesnikoff (USA, CAN)
Nordic Structures (USA, CAN)
Mercer Mass Timber
SmartLam
Sterling Structural
Superstructures répertoriées dans l'édition 32 de Lignatec « Bois lamellé-croisé de production suisse ».

En important une composition de la bibliothèque de structures en couches, tous les paramètres pertinents sont automatiquement adoptés. La base de données est continuellement mise à jour et enrichie.

Lire la suite

Le module complémentaire Vérification du bois pour RFEM 6 / RSTAB 9 est polyvalent et combine de nombreux éléments supplémentaires. [*S16332764*] Module complémentaire Calcul du bois pour RFEM 6

Lire la suite

Foire aux Questions (FAQ)

Comment les facteurs NDS et CSA O86 peuvent-ils être ajustés manuellement pour être considérés dans le module complémentaire Vérification du bois ?

Quel calcul est effectué pour les options « Calcul de la torsion » de la configuration pour la résistance NDS ?

Quels logiciels Dlubal recommandez-vous pour le calcul de structure, notamment les structures bois ?

Comment modéliser une poutre en bois avec des raidisseurs des deux côtés ? (éclisses)

Comment puis-je générer une charge surfacique sur des barres à l'aide de cellules dans RFEM 6 ou RSTAB 9 ?

Quels logiciels sont nécessaires pour calculer les structures en panneaux CLT, stratifiés et sandwich ?

Projets clients

Produits recommandés pour vous

RFEM 6 | Logiciel de base RFEM 6

RFEM 6

Logiciel de base

La nouvelle génération de logiciels aux éléments finis est utilisée pour le calcul de structures composées de barres, de surfaces et de solides.

Prix de la licence initiale 4 170,00 USD

RFEM 6 | Vérification

Vérification du bois pour RFEM 6

Module complémentaire

Le module complémentaire Vérification du bois permet d'effectuer les vérifications à l'état limite ultime, à l'état limite de service et de la résistance au feu des barres en bois selon diverses normes.

Prix de la licence initiale 1 930,00 USD

RFEM 6 | Analyse supplémentaire

Stabilité de structure pour RFEM 6

Module complémentaire

Le module complémentaire Stabilité de la structure permet d'effectuer l'analyse de stabilité des structures. Il détermine les facteurs de charge critiques et les modes de stabilité correspondants.

Prix de la licence initiale 1 300,00 USD

RSTAB 9 | Logiciel de base RSTAB 9

RSTAB 9

logiciel de calcul de structures filaires

Logiciel de base

Le logiciel de calcul de structures filaires 3D RSTAB pour le calcul statique et dynamique des charpentes en acier, en béton, en bois et en d'autres matériaux.

Prix de la licence initiale 2 910,00 USD

RSTAB 9 | Vérification

Vérification du bois pour RSTAB 9

Module complémentaire

Le module complémentaire Vérification du bois permet d'effectuer les vérifications à l'état limite ultime, à l'état limite de service et à la résistance au feu des barres en bois selon diverses normes.

Prix de la licence initiale 1 930,00 USD

RX-TIMBER 2 | Structures bois

RX-TIMBER Glued-Laminated Beam 2

Programme autonome

Calcul de poutres en lamellé-collé à travée simple et à grande portée selon l'Eurocode 5 ou DIN 1052

Prix de la licence initiale 1 120,00 USD

RX-TIMBER 2 | Structures bois

Poutre continue RX-TIMBER 2

Programme autonome

Calcul de poutres simples, continues et Gerber avec ou sans porte-à-faux selon l'Eurocode 5 ou la DIN 1052