Is this page helpful?

10774x

001656

Dipl.-Ing. (FH) René Flori

2020-09-11

Design of K-Type Joint Using CHS Sections According to EN 1993-1-8

Closed circular cross-sections are ideal for welded truss structures. The architecture of such constructions is popular when designing transparent roofs. This article shows the special features of the connection design using hollow sections.

1 Spatial Truss Girder

General

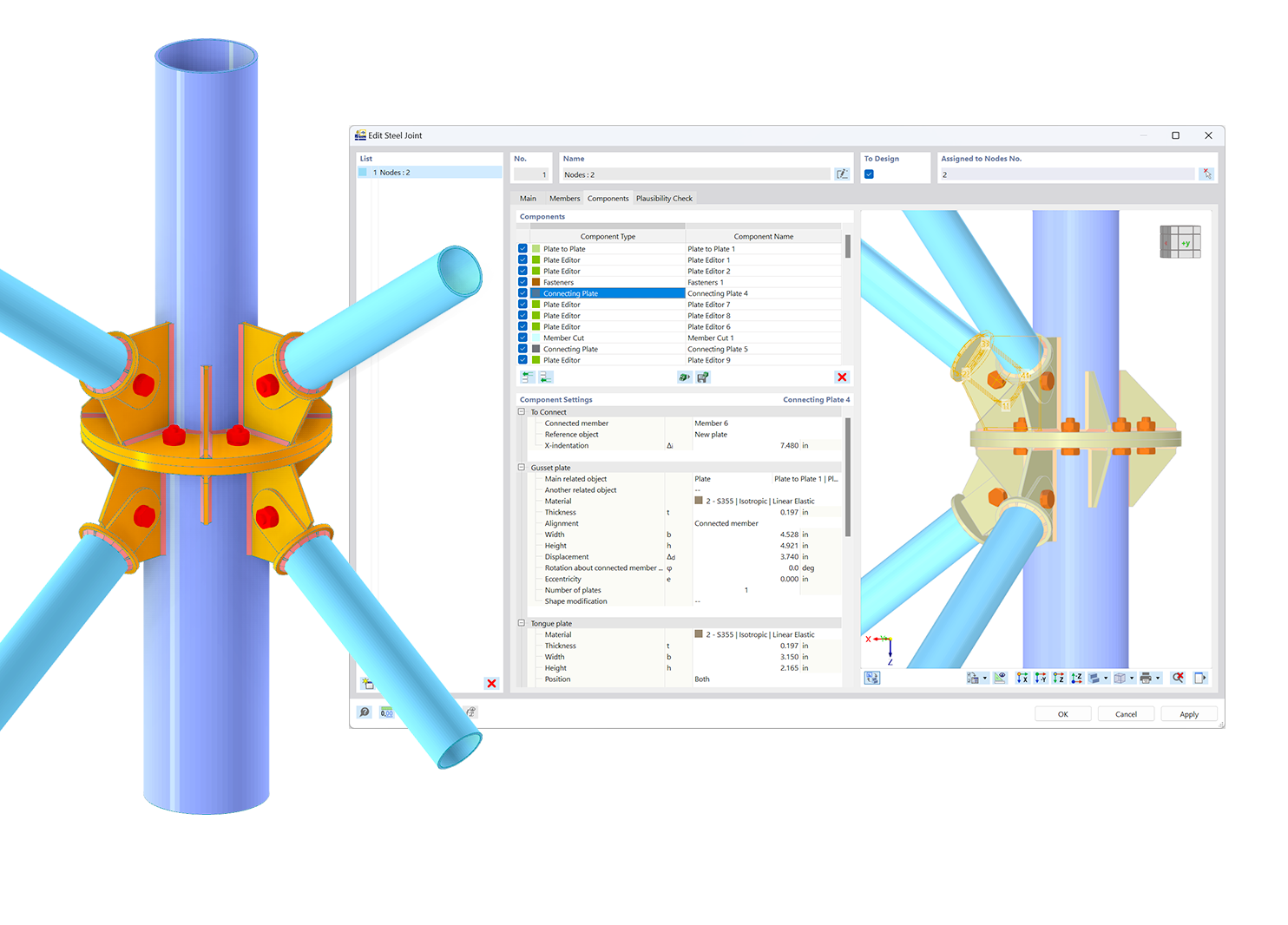
Slender truss structures made of closed cross-sections are popular in architecture. Due to computer-aided production of cuts and connection geometries, it is possible also to have complex spatial nodes. This technical article deals with the design of a K‑node. The node definition and the design, in particular, are described in detail.

Roof Structure Truss Girder Curved from CHS

2 Curved Spatial Truss Girders of Welded CHS

Details of Model

Material: S355
Chord cross-section: RO 108x6.3 | DIN 2448, DIN 2458
Strut cross-section: RO 60.3x4 | DIN 2448, DIN 2458
Dimensions: see the graphic

3 Truss Dimensions

Assigning Node to Joint Type

The connection type for a hollow section node is not only defined by the geometry, but also by the orientation of the axial forces in the struts. In our example, there is a tensile force in Member 35 (Strut 1) and a compression force in Member 36 (Strut 2) on Node 28 to be designed. Given this distribution of internal forces and moments, the joint type is a K‑node. If there was compression or tension in both struts, the connection type would be a Y‑node.

4 Distribution of Internal Forces for Axial Force

Checking Validity Limits

Compliance with the validity limits is crucial for any design. The ratio of the diameters of struts and chords is important. If it is not in the range of 0.2 ≤ d_i / d_o ≤ 1.0, it is impossible to perform the design. The diameter ratio d_i / d_o is also referred to as β. The European standard EN 1993-1-8 [1] specifies in Table 7.1 the validity limits for struts and chord members, as well as a limitation of the struts' overlap. If you want to have a gap between the struts, a minimum dimension of g ≥ t₁ + t₂ must be observed, too. t is the respective wall thickness of the struts. Structural components subjected to compression also need to be classified into cross-section classes 1 or 2. A corresponding check is carried out according to EN 1993-1-1 [2], Chapter 5.5.

5 Displaying Window 1.3 Geometry in RF-/HSS

Design

In our example, the connection meets the validity limits according to Table 7.1. Therefore, it is sufficient according to EN 1993-1-8, Section 7.4.1 (2), to analyze the chord member for flange failure and punching shear.

Flange Failure of Chord Member due to Axial Force According to EN 1993-1-8, Table 7.2, Row 3.2

Determination of Diameter-Wall Ratio γ

γ = \frac{d_{0}}{2 \cdot t_{0}}

γ	Verhältnis der Breite oder des Durchmessers des Gurtstabes zum zweifachen seiner Wanddicke
d₀	Gesamtdurchmesser Gurtstab
t₀	Wanddicke des Gurtstabquerschnitts

Determination of Diameter-Wall Thickness Ratio γ

γ = 8.57

Determination of Factor k_g

k_{g} = γ^{0.2} \cdot (1 + \frac{0.024 \cdot γ^{1.2}}{1 + e^{(0.5 \cdot g / t_{0} - 1.33)}})

k_g	Beiwert bei Knotenanschlüssen mit Spalt g
γ	Verhältnis der Breite oder des Durchmessers des Gurtstabes zum zweifachen seiner Wanddicke
e	Eulersche Zahl
g	Spaltweite zwischen den Streben eines K- oder N-Anschlusses
t₀	Wanddicke des Gurtstabquerschnitts

Factor k_g According to EN 1993-1-8, Table 7.2

k_g = 1.72

Determination of Chord Tension Coefficient k_p

k_{p} = 1 + 0.3 \cdot n_{p} \cdot (1 - n_{p})

n_{p} = \frac{f_{p}}{f_{y}}

f_{p} = \frac{N_{p}}{A_{0}} - \frac{|M_{0}|}{W_{0}}

k_p	Gurtvorspannungsbeiwert
n_p	Verhältniswert
f_p	Wert der einwirkenden Druckspannung im Gurtstab ohne die Spannungen infolge der Komponenten der Strebenkräfte am Anschluss parallel zum Gurt
f_y	Streckgrenze
N_p	Anlaufende Normaldruckkraft im Gurt
A₀	Querschnittsfläche Gurtstab
M₀	Sekundäres Moment aus Exzentrizität
W₀	Elastisches Widerstandsmoment des Gurtquerschnitts

Chord Prestress Coefficient k_p EN 1993-1-8

f_p is the chord tension from the axial force N_p and the additional moment from eccentricity. Since there is compression and tension in the chors, it is assumed that N_p = 0. Furthermore, the eccentricity of the joint is so small that an additional moment from any eccentric connection of the struts does not have to be considered. The auxiliary coefficient is thus zero. The sign convention for compression and tension forces in RFEM and RSTAB differs from those of the European standard EN 1993-1-8. Therefore, the formula is adjusted to k_p.
k_p = 1.0

Determination of Allowable Limit Internal Force N_Rd

N_{1, Rd} = \frac{k_{g} \cdot k_{p} \cdot f_{y 0} \cdot {t_{0}}^{2}}{\sin (θ_{1})} \cdot (1.8 + 10.2 \cdot \frac{d_{1}}{d_{0}}) / γ_{M 5}

N_{2, Rd} = \frac{\sin (θ_{1})}{\sin (θ_{2})} \cdot N_{1, Rd}

N_1,Rd	Bemessungswert der Normalkrafttragfähigkeit des Anschlusses für Strebe 1
k_g	Beiwert bei Knotenanschlüssen mit Spalt g
k_p	Gurtvorspannungsbeiwert
f_y0	Streckgrenze des Werkstoffs eines Gurtstabes
t₀	Wanddicke des Gurtstabquerschnitts
θ₁	Eingeschlossener Winkel zwischen Strebe 1 und Gurtstab
d₁	Gesamtdurchmesser Strebe 1
d₀	Gesamtdurchmesser Gurtstab
y_M5	Teilsicherheitsbeiwert
N_2,Rd	Bemessungswert der Normalkrafttragfähigkeit des Anschlusses für Strebe 2
θ₂	Eingeschlossener Winkel zwischen Strebe 2 und Gurtstab

Flange Failure According to EN 1993-1-8, Table 7.2, Row 3.2

N_1,Rd = N_2,Rd = 257.36 kN
N_1,Ed / N_1,Rd = 197.56 / 257.36 = 0.77 < 1.0
N_2,Ed / N_2,Rd = 186.89 / 257.36 = 0.73 < 1.0

Punching of Chord Member due to Axial Force According to EN 1993-1-8, Table 7.2, Row 4

Determination of Allowable Limit Internal Force N_Rd

N_{i, Rd} = \frac{f_{y 0}}{\sqrt{3}} \cdot t_{0} \cdot π \cdot d_{i} \cdot \frac{1 + \sin (θ_{i})}{2 \cdot \sin^{2} (θ_{i})} / γ_{M 5}

N_i,Rd	Bemessungswert der Normalkrafttragfähigkeit des Anschlusses für das Bauteil i
f_y0	Streckgrenze des Werkstoffs eines Gurtstabes
t₀	Wanddicke des Gurtstabquerschnitts
π	Kreiszahl
d_i	Gesamtdurchmesser bei KHP-Bauteilen i
θ_i	Eingeschlossener Winkel zwischen Strebe i und Gurtstab
γ_M5	Teilsicherheitsbeiwert

Punching Chord Member due to Axial Force According to EN 1993-1-8, Table 7.2, Row 4

N_1,Rd = N_2,Rd = 417.58 kN
N_1,Ed / N_1,Rd = 197.56 / 417.58 = 0.47 < 1.0
N_2,Ed / N_2,Rd = 186.89 / 417.58 = 0.45 < 1.0

Flange Failure of Chord Member due to Moment M_op According to EN 1993-1-8, Table 7.5, Row 2

This design is only relevant for 3D structures where moments may also occur from the truss plane.

Determination of Allowable Limit Internal Force M_op,Rd

M_{op, i, Rd} = \frac{f_{y 0} \cdot {t_{0}}^{2} \cdot d_{i}}{\sin (θ_{i})} \cdot \frac{2.7}{1 - 0.81 \cdot β} \cdot k_{p} / γ_{M 5}

M_op,i,Rd	Bemessungswert der Momententragfähigkeit des Anschlusses bei Biegung aus der Tragwerksebene für das Bauteil i
f_y0	Streckgrenze des Werkstoffs eines Gurtstabes
t₀	Wanddicke des Gurtstabquerschnitts
d_i	Gesamtdurchmesser bei KHP-Bauteilen i
θ_i	Eingeschlossener Winkel zwischen Strebe i und Gurtstab
β	Verhältnis der mittleren Durchmesser oder mittleren Breiten von Strebe und Gurtstab
k_p	Gurtvorspannungsbeiwert
y_M5	Teilsicherheitsbeiwert

Flange Failure of Chord Member due to Moment Mₒₚ According to EN 1993-1-8, Table 7.5, Row 2

M_op,1,Rd = M_op,2,Rd = 5.92 kNm
M_op,1,Ed / M_op,1,Rd = 0.08 / 5.92 = 0.01 < 1.0
M_op,2,Ed / M_op,2,Rd = 0.01 / 5.92 = 0.00 < 1.0

Flange Failure of Chord Member due to Moment M_ip According to EN 1993-1-8, Table 7.5, Row 1

Determination of Allowable Limit Internal Force M_ip,Rd

M_{ip, i, Rd} = 4.85 \cdot \frac{f_{y 0} \cdot {t_{0}}^{2} \cdot d_{i}}{\sin (θ_{i})} \cdot \sqrt{γ} \cdot β \cdot k_{p} / γ_{M 5}

M_ip,i,Rd	Bemessungswert der Momententragfähigkeit des Anschlusses bei Biegung in der Tragwerksebene für das Bauteil i
f_y0	Streckgrenze des Werkstoffs eines Gurtstabes
t₀	Wanddicke des Gurtstabquerschnitts
d_i	Gesamtdurchmesser bei KHP-Bauteilen i
θ_i	Eingeschlossener Winkel zwischen Strebe i und Gurtstab
γ	Verhältnis der Breite oder des Durchmessers des Gurtstabes zum zweifachen seiner Wanddicke
β	Verhältnis der mittleren Durchmesser oder mittleren Breiten von Strebe und Gurtstab
k_p	Gurtvorspannungsbeiwert
γ_M5	Teilsicherheitsbeiwert

Flange Failure of Chord Member due to Moment Mᵢₚ According to EN 1993-1-8, Table 7.5, Row 1

M_ip,1,Rd = M_ip,2,Rd = 9.53 kNm
M_ip,1,Ed / M_ip,1,Rd = 0.37 / 9.53 = 0.04 < 1.0
M_ip,2,Ed / M_ip,2,Rd = 0.14 / 9.53 = 0.01 < 1.0

Punching of Chord Member due to Moment M_op According to EN 1993-1-8, Table 7.5, Row 3.2

This design is only relevant for 3D structures where moments may also occur from the truss plane.

Determination of Allowable Limit Internal Force M_op,Rd

M_{op, i, Rd} = \frac{f_{y 0} \cdot t_{0} \cdot {d_{i}}^{2}}{\sqrt{3}} \cdot \frac{3 + \sin (θ_{i})}{4 \cdot \sin^{2} (θ_{i})} / γ_{M 5}

M_op,i,Rd	Bemessungswert der Momententragfähigkeit des Anschlusses bei Biegung aus der Tragwerksebene für das Bauteil i
f_y0	Streckgrenze des Werkstoffs eines Gurtstabes
t₀	Wanddicke des Gurtstabquerschnitts
d_i	Gesamtdurchmesser bei KHP-Bauteilen i
θ_i	Eingeschlossener Winkel zwischen Strebe i und Gurtstab
y_M5	Teilsicherheitsbeiwert

Punching of Chord Member due to Moment M_op According to EN 1993-1-8, Table 7.5, Row 3.2

M_op,1,Rd = M_op,2,Rd = 8.70 kNm
M_op,1,Ed / M_op,1,Rd = 0.08 / 8.70 = 0.01 < 1.0
M_op,2,Ed / M_op,2,Rd = 0.01 / 8.70 = 0.00 < 1.0

Punching of Chord Member due to Moment M_ip According to EN 1993-1-8, Table 7.5, Row 3.1

Determination of Allowable Limit Internal Force M_ip,Rd

M_{ip, i, Rd} = \frac{f_{y 0} \cdot t_{0} \cdot {d_{i}}^{2}}{\sqrt{3}} \cdot \frac{1 + 3 \cdot \sin (θ_{i})}{4 \cdot \sin^{2} (θ_{i})} / γ_{M 5}

M_ip,i,Rd	Bemessungswert der Momententragfähigkeit des Anschlusses bei Biegung in der Tragwerksebene für das Bauteil i
f_y0	Streckgrenze des Werkstoffs eines Gurtstabes
t₀	Wanddicke des Gurtstabquerschnitts
d_i	Gesamtdurchmesser bei KHP-Bauteilen i
θ_i	Eingeschlossener Winkel zwischen Strebe i und Gurtstab
y_M5	Teilsicherheitsbeiwert

Punching of Chord Member due to Moment M_ip According to EN 1993-1-8, Table 7.5, Row 3.1

M_ip,1,Rd = M_ip,2,Rd = 7.33 kNm
M_ip,1,Ed / M_ip,1,Rd = 0.37 / 7.33 = 0.05 < 1.0
M_ip,2,Ed / M_ip,2,Rd = 0.14 / 7.33 = 0.02 < 1.0

Interaction Conditions According to EN 1993-1-8, Chapter 7.4.2, Equation 7.3

In this design step, the struts are designed for the shared loading from axial force and bending. Currently, only bending perpendicular to the truss plane is considered here.

\frac{N_{i, Ed}}{N_{i, Rd}} + \frac{|M_{op, i, Ed}|}{M_{op, i, Rd}} \leq 1.0

\frac{197.56}{257.36} + \frac{|- 0.08|}{5.92} = 0.78 < 1.0 (S 1)

\frac{- 186.89}{257.36} + \frac{|- 0.01|}{5.92} = 0.72 < 1.0 (S 2)

N_i,Ed	Bemessungswert der einwirkenden Normalkraft für das Bauteil i
N_i,Rd	Bemessungswert der Normalkrafttragfähigkeit des Anschlusses für das Bauteil i
M_op,i,Ed	Bemessungswert des einwirkenden Momentes aus der Tragwerksebene für das Bauteil i
M_op,i,Rd	Bemessungswert der Momententragfähigkeit des Anschlusses bei Biegung aus der Tragwerksebene für das Bauteil i
S1	Strebe 1
S2	Strebe 2

Interaction Conditions According to EN 1993-1-8, Section 7.4.2, Equation 7.3

Conclusion

The technical article shows that the design for a K-node is not trivial. With the RF-/HSS add-on module, Dlubal offers a tool for designing all nodal types defined in the European standard, for CHS as well as SHS and RHS sections.

Knowledge Base

KB 001656 | Design of K-Type Joint Using CHS-Sections According to EN 1993-1-8

Author

Mr. Flori is the customer support team leader and provides technical support for customers of Dlubal Software.

Links

References

European Committee for Standardization. (2009). Eurocode 3: Design of Steel Structures – Part 1-8: Design of Joints; EN 1993‑1‑8:2005 + AC:2009. Berlin: Beuth Verlag GmbH.
DIN. (1993). Eurocode 3: Design of Steel Structures – Part 1‑1: General Rules and Rules for Buildings, EN 1993-1-1:2005. Berlin: Beuth Verlag GmbH.

Downloads

Model of Technical Article | RFEM 5 File

3.98 MB

Recommended Products for You

RFEM 6 | Main Program RFEM 6

RFEM 6

Main Program

The new generation of 3D FEA software is used for the structural analysis of members, surfaces, and solids.

Price of First License 4,790.00 USD

RFEM 6 | Design

Steel Design for RFEM 6

Add-On

The Steel Design add-on performs the ultimate and serviceability limit state design checks of steel members according to various standards.

Price of First License 2,970.00 USD

RFEM 6 | Joints

Steel Joints for RFEM 6

Add-On

The Steel Joints add-on for RFEM allows you to analyze steel connections using an FE model. The FE model is generated automatically in the background and can be controlled via the simple and familiar input of components.

Price of First License 2,670.00 USD

RFEM 6 | Additional Analysis

Torsional Warping (7 DOF) for RFEM 6

Deformation analysis of a rod subjected to warping torsion loads, showcasing the resulting structural behavior.

Add-On

The Torsional Warping (7 DOF) add-on allows you to consider cross-section warping as an additional degree of freedom.

Price of First License 1,660.00 USD

RFEM 6 | Additional Analysis

Nonlinear Material Behavior for RFEM 6

Add-On

The Nonlinear Material Behavior add-on allows you to consider material nonlinearities in RFEM for example, isotropic plastic, orthotropic plastic, isotropic damage).

Price of First License 1,660.00 USD

RFEM 6 | Additional Analysis

Structure Stability for RFEM 6

Add-On

The Structure Stability add-on performs stability analysis of structures. It determines critical load factors and the corresponding stability modes.

Price of First License 1,460.00 USD

RFEM 6 | Additional Analysis

Construction Stages Analysis (CSA) for RFEM 6

Add-On

The Construction Stages Analysis (CSA) add-on allows for considering the construction process of structures (member, surface, and solid structures) in RFEM.

Price of First License 1,760.00 USD

RFEM 6 | Additional Analysis

Time-Dependent Analysis (TDA) for RFEM 6

Add-On

The Time-Dependent Analysis (TDA) add-on allows you to consider the time-dependent material behavior of members and surfaces. The long-term effects, such as creep, shrinkage, and aging, can influence the distribution of internal forces, depending on the structure.

Price of First License 1,160.00 USD

RFEM 6 | Additional Analysis

Form-Finding for RFEM 6

Add-On

The Form-Finding add-on finds the optimal shape of members subjected to axial forces and tension-loaded surface models. The shape is determined by the equilibrium between the member axial force or the membrane stress and the existing boundary conditions.

Price of First License 2,320.00 USD

RFEM 6 | Dynamic Analysis

Modal Analysis for RFEM 6

Add-On

The Modal Analysis add-on allows for the calculation of eigenvalues, natural frequencies, and natural periods for member, surface, and solid models.

Price of First License 1,360.00 USD

RFEM 6 | Dynamic Analysis

Pushover Analysis for RFEM 6

Add-On

Using the Pushover Analysis add-on, you can analyze the seismic actions on a particular building, and thus assess whether the building can withstand an earthquake.

Price of First License 1,460.00 USD

RFEM 6 | Special Solutions

Building Model for RFEM 6

Add-On

The Building Model add-on for RFEM allows you to define and manipulate a building using stories. The stories can be adjusted in many ways afterwards. The information about stories and the entire model (center of gravity) is displayed in tables and graphics.

Price of First License 1,970.00 USD

RFEM 6 | Design

Stress-Strain Analysis for RFEM 6

Add-On

The Stress-Strain Analysis add-on performs general stress analysis by calculating the existing stresses and comparing them with the limit stresses.

Price of First License 1,360.00 USD

RSTAB 9 | Main Program RSTAB 9

RSTAB 9

Structural Frame and Truss Analysis Software

Main Program

The modern 3D structural analysis and design program is suitable for the structural and dynamic analysis of beam structures as well as the design of concrete, steel, timber, and other materials.

Price of First License 3,380.00 USD

RSTAB 9 | Design

Steel Design for RSTAB 9

Add-On

The Steel Design add-on performs the ultimate and serviceability limit state design checks of steel members according to various standards.

Price of First License 2,970.00 USD

RSTAB 9 | Additional Analysis

Structure Stability for RSTAB 9

Add-On

The Structure Stability add-on performs the stability analysis of structures. It determines critical load factors and the corresponding stability modes.

Price of First License 1,460.00 USD

RSTAB 9 | Design

Stress-Strain Analysis for RSTAB 9

Add-On

The Stress-Strain Analysis add-on performs a general stress analysis by calculating the existing stresses and comparing them to the limit stresses.

Price of First License 1,260.00 USD

RSTAB 9 | Additional Analysis

Torsional Warping (7 DOF) for RSTAB 9

Add-On

The Torsional Warping (7 DOF) add-on allows for considering cross-section warping as an additional degree of freedom when calculating members.

Price of First License 1,660.00 USD

RSTAB 9 | Dynamic Analysis

Modal Analysis for RSTAB 9

Add-On

The Modal Analysis add-on allows for the calculation of eigenvalues, natural frequencies, and natural periods for member, surface, and solid models.

Price of First License 1,360.00 USD

RSTAB 9 | Dynamic Analysis

Pushover Analysis for RSTAB 9

Add-On

Earthquakes may have a significant impact on the deformation behavior of buildings. A pushover analysis allows you to analyze the deformation behavior of buildings and compare them with seismic actions. Using the Pushover Analysis add-on, you can analyze the seismic actions on a particular building, and thus assess whether the building can withstand the earthquake.

Price of First License 1,460.00 USD

RFEM 6 | Special Solutions

Multilayer Surfaces (e.g. Laminate, CLT) for RFEM 6

Add-On

The Multilayer Surfaces add-on allows you to define multilayer surface structures. The calculation can be carried out with or without the shear coupling.

Price of First License 1,560.00 USD

RFEM 6 | Special Solutions

Optimization & Cost / CO2 Emission Estimation for RFEM 6

3D Model of the Vocational School in RFEM (© Eggers Tragwerksplanung GmbH)

Add-On

The two-part Optimization & Costs / CO2 Emission Estimation add-on finds suitable parameters for parameterized models and blocks via the artificial intelligence (AI) technique of particle swarm optimization (PSO) for compliance with common optimization criteria. Furthermore, this add-on estimates the model costs or CO2 emissions by specifying unit costs or emissions per material definition for the structural model.

Price of First License 1,660.00 USD

RFEM 6 | Design

Concrete Design for RFEM 6

Add-On

The Concrete Design add-on allows for various design checks according to international standards. You can design members, surfaces, and columns, as well as perform punching and deformation analyses.

Price of First License 2,970.00 USD

RFEM 6 | Design

Timber Design for RFEM 6

Add-On

The Timber Design add-on performs the ultimate, serviceability, and fire resistance limit state design checks of timber members according to various standards.

Price of First License 2,170.00 USD

RFEM 6 | Design

Masonry Design for RFEM 6

Add-On

The Masonry Design add-on for RFEM allows you to design masonry using the finite element method. It was developed as part of the research project titled DDMaS – Digitizing the Design of Masonry Structures. The material model represents the nonlinear behavior of the brick-mortar combination in the form of macro-modeling.

Price of First License 1,860.00 USD

RFEM 6 | Design

Aluminum Design for RFEM 6

Visual analysis showing deformation in an aluminum hall structure. Detailed depiction of structural response to forces.

Add-On

The Aluminum Design add-on performs the ultimate and serviceability limit state design checks of aluminum members according to various standards.

Price of First License 1,970.00 USD

RSTAB 9 | Special Solutions

Optimization & Cost / CO2 Emission Estimation for RSTAB 9

Add-On

Price of First License 1,660.00 USD

RSTAB 9 | Design

Concrete Design for RSTAB 9

Add-On

Concrete Design add-on allows for various design checks of members and columns according to international standards.

Price of First License 2,970.00 USD

RSTAB 9 | Design

Timber Design for RSTAB 9

Add-On

The Timber Design add-on performs the ultimate, serviceability, and fire resistance limit state design checks of timber members according to various standards.

Price of First License 2,170.00 USD

RSTAB 9 | Design

Aluminum Design for RSTAB 9

Add-On

The Aluminum Design add-on performs the ultimate and serviceability limit state design checks of aluminum members according to various standards.

Price of First License 1,970.00 USD

Display Product Family

Design of K-Type Joint Using CHS Sections According to EN 1993-1-8

General

Details of Model

Assigning Node to Joint Type

Checking Validity Limits

Design

Flange Failure of Chord Member due to Axial Force According to EN 1993-1-8, Table 7.2, Row 3.2

Punching of Chord Member due to Axial Force According to EN 1993-1-8, Table 7.2, Row 4

Flange Failure of Chord Member due to Moment Mop According to EN 1993-1-8, Table 7.5, Row 2

Flange Failure of Chord Member due to Moment Mip According to EN 1993-1-8, Table 7.5, Row 1

Punching of Chord Member due to Moment Mop According to EN 1993-1-8, Table 7.5, Row 3.2

Punching of Chord Member due to Moment Mip According to EN 1993-1-8, Table 7.5, Row 3.1

Interaction Conditions According to EN 1993-1-8, Chapter 7.4.2, Equation 7.3

Conclusion

Flange Failure of Chord Member due to Moment M_op According to EN 1993-1-8, Table 7.5, Row 2

Flange Failure of Chord Member due to Moment M_ip According to EN 1993-1-8, Table 7.5, Row 1

Punching of Chord Member due to Moment M_op According to EN 1993-1-8, Table 7.5, Row 3.2

Punching of Chord Member due to Moment M_ip According to EN 1993-1-8, Table 7.5, Row 3.1