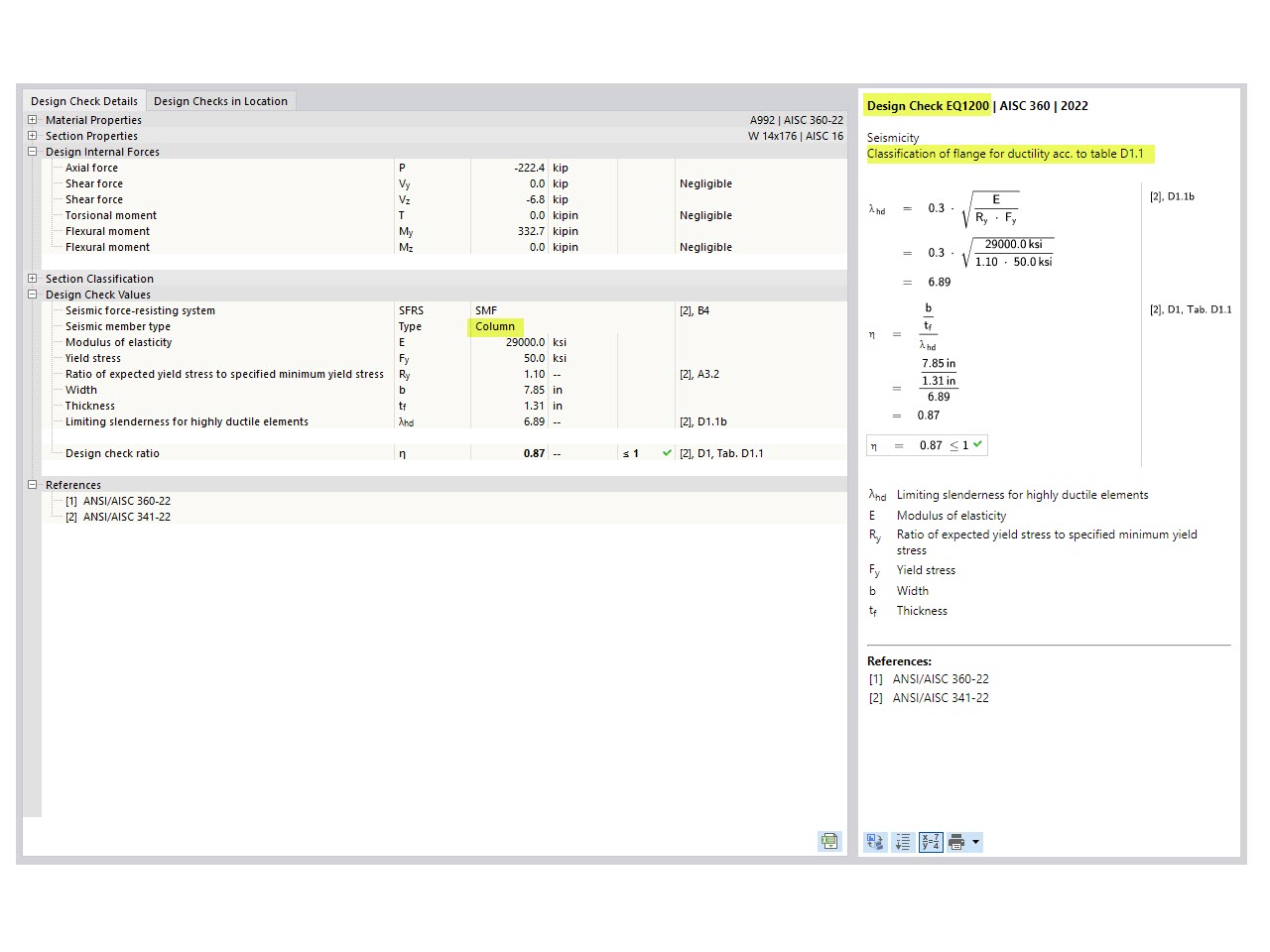
General
The total settlement stot on soil caused by structural loads consists of the components of the immediate settlement s0, consolidation settlement s1, and the time-dependent creep settlement s2.
stot = s0 + s1 + s2 = s + s2
According to DIN 4019 [2], the method described below includes a specific setting "s" consisting of both settlement components – settlement caused by consolidation and settlement caused by creep (secondary settlement). Image 01 shows the time-dependent settlement components graphically. In this case, the time t0 represents the period until complete consolidation occurs.
![Time-Dependent Settlement Components [2]](/en/webimage/009673/2419908/01-en-png-png.png)
Settlement Calculation Using Vertical Stresses on Soil
The settlement calculation method described below is based on the model of an elastic, isotropic, homogeneous half-space. This calculation approach can also be applied for the settlement of foundation soil with several layers.
To determine the settlement, it is necessary to divide the soil into strips and define the vertical soil stresses beneath the foundation base. Based on the elasticity analysis, the specific settlements si are determined for each strip; these are then added together to obtain the total settlement s.
where
Δσz,i is the additional stress-generating settlement in strip i,
ES,i is the stiffness modulus of strip i,
Δzi is the thickness of strip i.
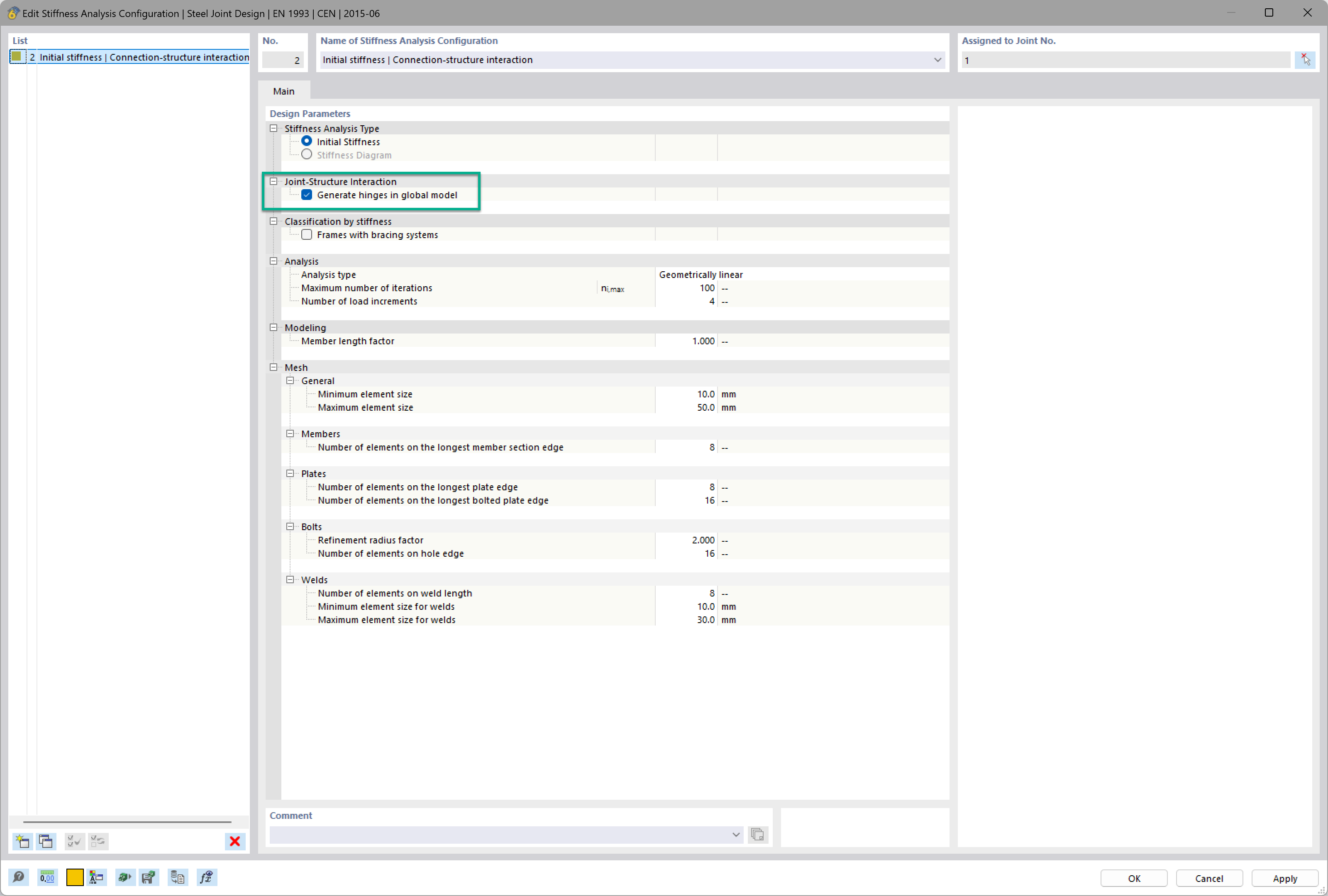
Determination of Vertical Soil Stresses
First, the settlement calculation requires the determination of vertical soil stresses. The stress and settlement calculation is based on a model of the elastic isotropic half-space. The respective stresses can be distinguished according to their cause as follows:
σor is the soil stress caused by the soil self-weight
σz is the stress caused by a structural load
σz,i is the stress caused by the structural load in strip i
The vertical soil stresses σz due to the additional load at depth z can be calculated on the basis of the Boussinesq approach [3] and the superposition principle.
According to Boussinesq, the vertical stress on soil caused by the vertical concentrated load V is calculated on the half-space surface as shown in Image 02.
![Vertical Soil Stress According to Boussinesq [2]](/en/webimage/009674/2419912/02-en-png-png.png)
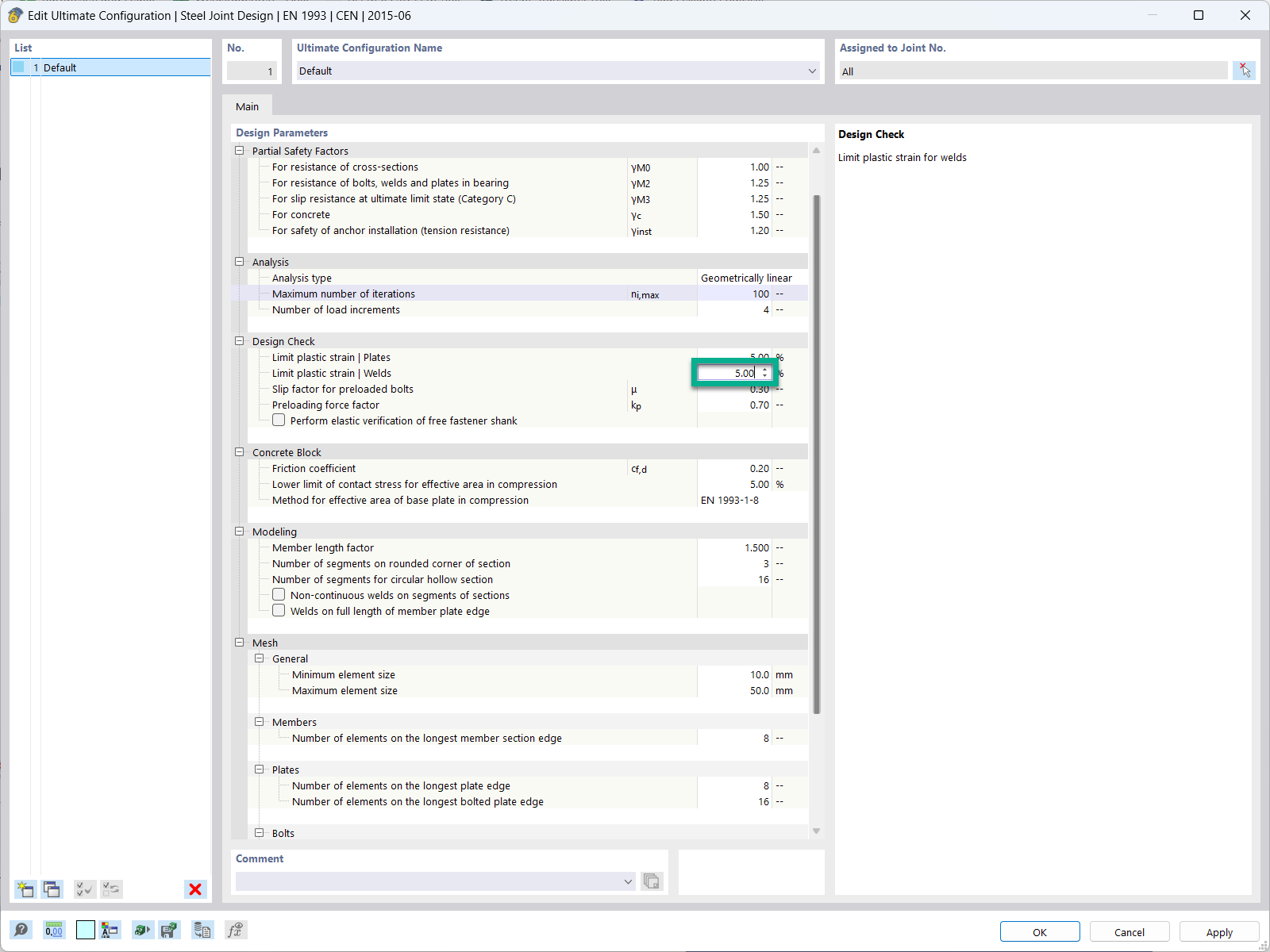
The vertical soil stresses at depth z under the corner point of a uniform "elastic" rectangle stress σz can be determined according to Image 03.
![Vertical Soil Stress Under Corner Point of Uniform Rectangular Load [2]](/en/webimage/009675/2419916/03-en-png-png.png)
The stress influence coefficient iR can be deduced from the corresponding nomograms, for example from DIN 4019 [2].
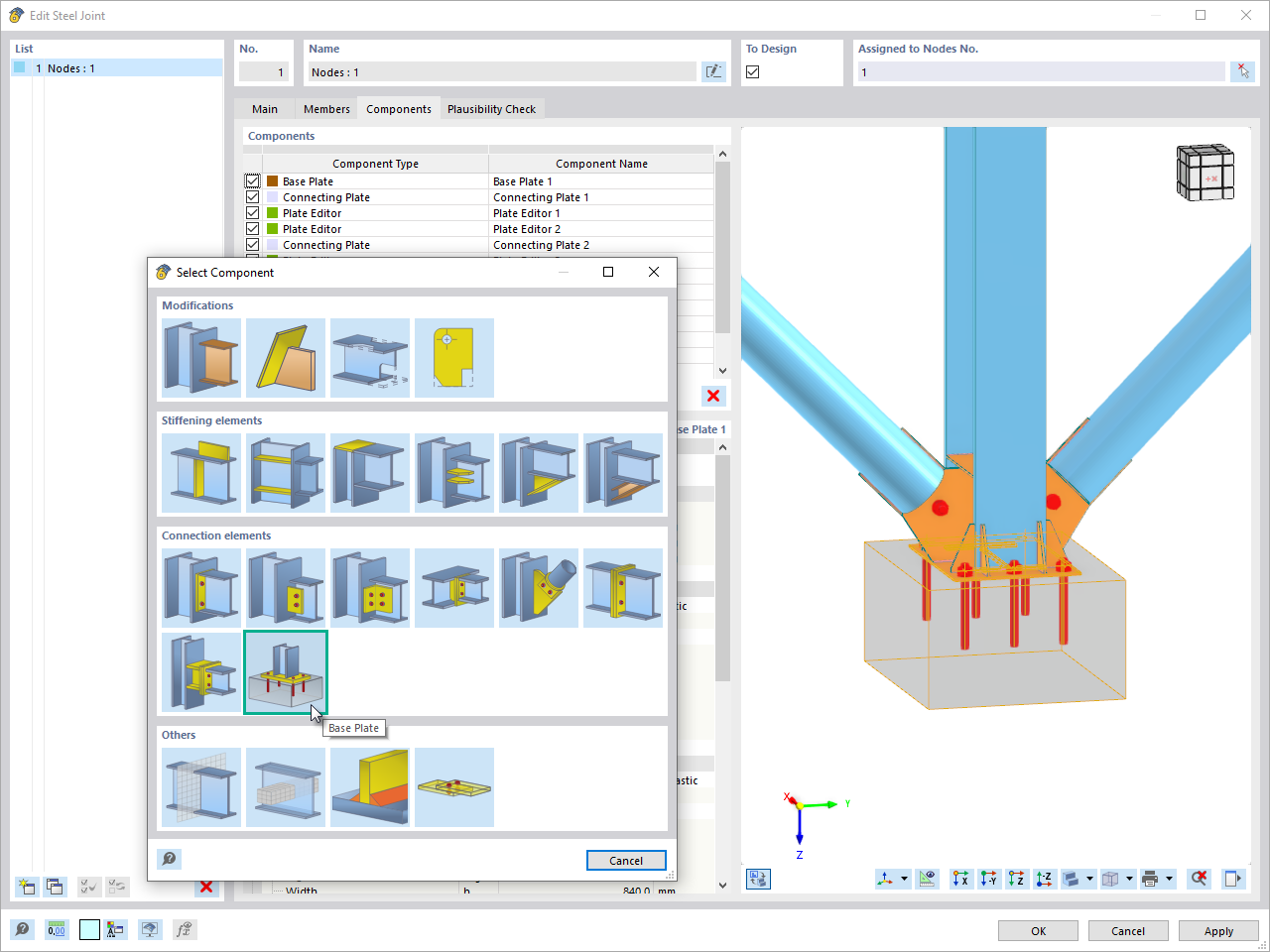
By applying the approach mentioned above, you obtain the result of the vertical soil stress distribution on the soil under the foundation, which is symbolically represented in Image 04.
![Distribution of Vertical Soil Stresses and Related Settlement Under Uniformly Distributed Load from [2]](/en/webimage/009676/2419920/04-en-png-png.png)
Settlement Depth
In the settlement calculation, it is necessary to consider additional stresses due to the foundation load up to the influence depth of the settlement, also called limit depth. According to EN 1997-1 [1] and DIN 4019 [2], the settlement influence depth may be taken as the depth z, at which the effective vertical stresses due to the foundation load are 20% of the effective initial vertical stresses in the soil.