Nastavení pro modální analýzu ( MOS ) určuje pravidla, podle kterých se vypočítají vlastní čísla. Přednastaveny jsou dva standardní typy analýzy. Tyto typy lze kdykoli upravit nebo vytvořit další nastavení pro modální analýzu.
Základní údaje
V záložce Základní údaje se spravují nastavení potřebná pro modální analýzu a některé další základní parametry výpočtu. Programy RFEM a RSTAB nabízejí různé možnosti pro výběr metody vlastních čísel.
Metoda vlastních čísel
V této sekci můžete definovat, která metoda se použije pro analýzu úlohy vlastních čísel a kolik vlastních tvarů se stanoví.
Metoda stanovení počtu tvarů
V seznamu máme na výběr ze tří možností.
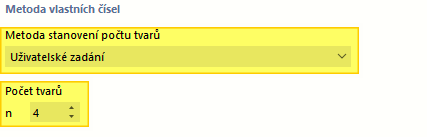
- Uživatelské zadání
Uživatelsky definovaná metoda umožňuje zadat počet nejmenších tvarů, které se mají vypočítat. Definovat lze až 9 999 vlastních tvarů. Kromě tohoto omezení představuje model také omezení počtu možných vlastních tvarů: Odpovídá stupňům volnosti, které vyplývají z počtu volných hmotných bodů vynásobených počtem směrů, ve kterých hmoty působí.
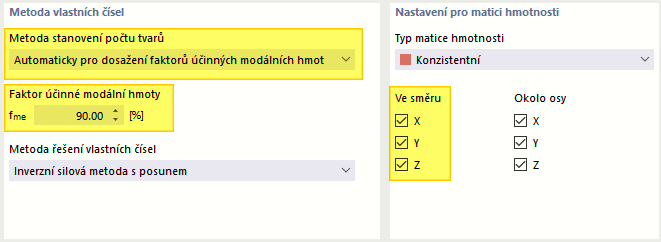
- Automaticky pro dosažení faktorů účinných modálních hmot
Program stanoví tolik vlastních tvarů, kolik je třeba, dokud není dosaženo zadaného součinitele modálních hmot. Součinitele účinných modálních hmot se analyzují pro zadané směry posunu (X, Y, Z).
- Automaticky pro dosažení maximální vlastní frekvence
Program stanoví tolik vlastních tvarů, kolik je třeba, dokud není dosaženo zadané vlastní frekvence.
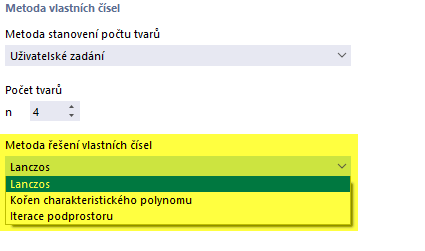
Metoda řešení problému vlastních čísel (pro RFEM)
V seznamu jsou k dispozici tři metody řešení úlohy vlastních čísel. Pokud jste nastavili automatickou metodu stanovení počtu vlastních čísel, je k dispozici pouze jedna metoda řešení.
Další informace o jednotlivých metodách najdete v kapitolách Bathe [1] a Natke [2].
- Lanczos
Lanczosova metoda je vhodná jako iterační metoda pro stanovení nejmenších vlastních čísel a příslušných vlastních tvarů velkých modelů. Ve většině případů tento algoritmus umožňuje dosáhnout rychlé konvergence. Lze spočítat až n–1 vlastních tvarů ( n : stupně volnosti modelu s hmotou).
Úvodní popis lze najít na cs.wikipedia.org/wiki/Lanczos_algorithm.
- Kořen charakteristického polynomu
Touto metodou se analytické řešení úlohy vlastních čísel provádí přímou metodou. Hlavní výhodou této metody je přesnost vyšších vlastních čísel a skutečnost, že lze stanovit všechna vlastní čísla modelu. U větších modelů může být tato metoda poměrně časově náročná.
Úvodní popis lze najít na cs.wikipedia.org/wiki/Characteristic_polynomial.
- Iterace podprostoru
Touto metodou se stanoví všechna vlastní čísla v jednom kroku. V tomto případě má spektrum matice tuhosti velký vliv na dobu výpočtu. Proto se tato metoda doporučuje pouze pro velké modely konečných prvků, pokud chceme spočítat několik vlastních čísel. Pracovní paměť omezuje počet vlastních čísel, která lze stanovit v rozumném čase.
Úvodní popis lze najít na cs.wikipedia.org/wiki/Krylov_subspace.
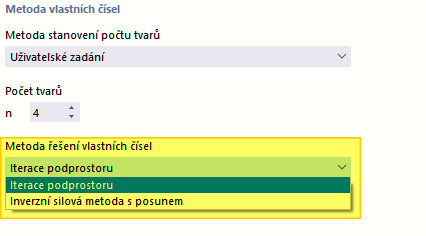
Metoda řešení problému vlastních čísel (pro RSTAB)
V seznamu jsou k dispozici dvě metody řešení úlohy vlastních čísel. Pokud jste zadali některou z automatických metod pro stanovení počtu vlastních čísel, je k dispozici pouze jedna metoda řešení.
Další informace o jednotlivých metodách najdete v článku Bathe [1].
- Iterace podprostoru
Touto metodou se stanoví všechna vlastní čísla v jednom kroku. V tomto případě má spektrum matice tuhosti velký vliv na dobu výpočtu. Proto se tato metoda doporučuje pouze pro velké modely konečných prvků, pokud chceme spočítat několik vlastních čísel. Pracovní paměť omezuje počet vlastních čísel, která lze stanovit v rozumném čase.
Úvodní popis lze najít na cs.wikipedia.org/wiki/Krylov_subspace.
- Inverzní silová metoda s posunem (Shifted inverse iteration)
Tato metoda je založena na předpokladech pro vlastní tvary vlastních tvarů, které se během výpočtu iteračně aproximují ke konvergentnímu řešení. Výhodou této metody je krátká doba výpočtu díky rychlé konvergenci. „Posun“ znamená, že touto metodou lze také stanovit všechny výsledky mezi největšími a nejmenšími vlastními čísly dané matice.
Úvodní popis lze najít na cs.wikipedia.org/wiki/Inverse_iteration.
Nastavení pro matici hmotnosti
V této sekci dialogu lze stanovit, která matice hmot se použije a ve kterých osách nebo okolo kterých mají hmoty při modální analýze působit.
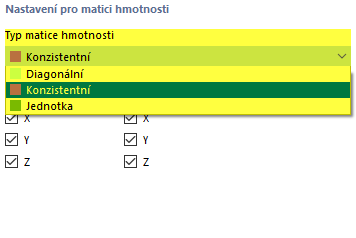
typ matice hmotnosti
V seznamu jsou k dispozici tři typy matic hmot.
- Diagonální
V případě diagonální matice hmot M se předpokládá, že hmoty jsou soustředěny v uzlech sítě konečných prvků. Vstupem do matice jsou soustředěné hmoty v translačních směrech X, Y a Z a také směry rotace okolo globálních os X (φX ), Y (φY ) a Z (φZ ). Je třeba rozlišovat následující dva případy:
– Diagonální matice pouze s translačními stupni volnosti: Pokud jsou pro diagonální matici aktivovány pouze translační směry, zobrazí se diagonální matice:
– Diagonální matice s translačními a rotačními stupni volnosti: Pokud jsou aktivovány translační směry a směry rotace, zobrazí se diagonální matice:
|
m |
Hmotnost |
|
IX, IY, IZ |
Momenty setrvačnosti hmot (RFEM 6) |
- Konzistentní
Konzistentní hmotová matice je kompletní hmotová matice konečných prvků. Hmoty se tak nesoustředí v uzlu sítě KP. Místo toho se používají tvarové funkce pro realističtější rozdělení hmot v konečných prvcích. Pomocí této matice hmot se zohledňují nediagonální vstupy v matici, takže se obecně zohledňuje natočení hmot. Konzistentní hmotová matice má následující strukturu (tvarové funkce se pro zjednodušení zanedbávají):
- Jednotka
Jednotková matice přepíše všechny dříve definované hmoty. Tato matice je konzistentní, kde všechny diagonální prvky mají hodnotu 1 kg. Hmota je nastavena na 1 v každém uzlu sítě KP. Zohledňují se posuny a natočení hmot. Tento matematický přístup by měl být použit pouze pro numerickou analýzu.
Další informace o typech matic a zejména o použití jednotkové matice lze najít v publikaci Barth/Rustler [3].
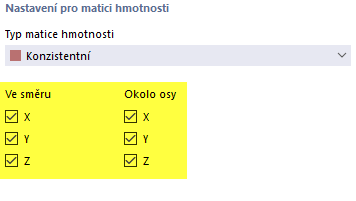
Ve směru/Okolo osy
Šest zaškrtávacích políček určuje, v kterém směru resp. okolo kterých os budou hmoty působit při stanovení vlastních čísel. Hmoty mohou působit v globálních směrech posunu X, Y nebo Z a mohou se natáčet okolo os X, Y a Z. Zaškrtněte příslušná políčka. Pro výpočet vlastních čísel je nutné aktivovat alespoň jeden směr nebo osu.
Možnosti
Poslední sekce v záložce "Základní údaje" nabízí důležitou možnost nastavení pro modální analýzu.
Najít vlastní tvary s frekvencí vyšší než
Pokud mají jednotlivé pruty nebo plochy v modelu velmi nízkou vlastní frekvenci, objeví se nejdříve jako lokální vlastní tvary. Pokud je zaškrtávací políčko zaškrtnuto, budou se počítat pouze vlastní čísla nad určitou hodnotou "f" vlastní frekvence. Tímto způsobem lze snížit počet výsledků a omezit ho na vlastní čísla, která jsou relevantní pro globální model.
Nastavení
V záložce Nastavení lze provést další nastavení pro modální analýzu a také základní parametry výpočtu.
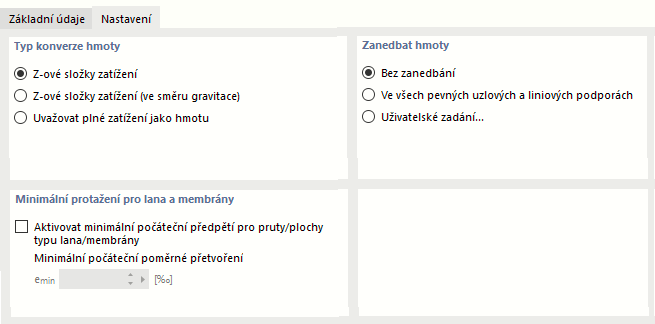
Typ konverze hmoty
V této sekci se řídí import hmot pro modální analýzu. Standardně se zohledňují pouze "'Z-složky zatížení". Jedná se o složky zatížení působící v obou směrech osy Z - kladné i záporné.
Při výběru možnosti "Složky zatížení Z (ve směru gravitace)" program použije pouze složky zatížení, které působí ve směru gravitace. Tíha je dána orientací globální osy Z (viz kapitola Orientace osy manuálu k programu RFEM): Působí ve směru globální osy Z, pokud směřuje dolů. Pokud globální osa Z směřuje nahoru, má to opačný účinek
Výběrem možnosti "Celá zatížení jako hmota" se importují všechna zatížení a všechny komponenty se použijí jako hmoty.
Zanedbání hmoty
Modální analýza zohledňuje všechny hmoty definované v modelu. V této sekci je možné zanedbat hmotu částí modelu, jako je hmota ve všech pevných uzlových a liniových podporách. Objekty lze vybrat i uživatelsky.
Při výběru možnosti "Uživatelské zadání" se zobrazí další záložka "Zanedbat hmoty". Zde můžete zadat objekty bez hmot.
Seznam objektů (uzlů, linií, prutů atd.) lze vytvořit přímo pomocí čísel objektů. Alternativně použijte
![]() v poli "Seznam objektů" pro grafický výběr objektů. Klikněte na tlačítko
v poli "Seznam objektů" pro grafický výběr objektů. Klikněte na tlačítko
![]() pro přednastavení pouze pevných podpor.
pro přednastavení pouze pevných podpor.
Pomocí zaškrtávacích políček pro směry posunů uX, uY a uZ a pro natočení φX, φY a φZ určíme, ve kterém směru se mají hmoty zanedbat.
Tuhost těles, jejichž hmoty jsou zanedbány, se přesto v matici zohlední. Pokud chcete zanedbat také tuhost těchto objektů, můžete pomocí Změna konstrukce upravit tuhosti individuálně. Objekty pro výpočet lze také deaktivovat (viz kapitola Main manuálu k programu RFEM).
Minimální protažení pro lana a membrány
Správné zadání lanové pruty a membránových ploch vyžaduje minimální změnu délky. Pokud je mezní hodnota nastavena příliš nízko, nejsou dosažené vlastní tvary realistické a stanoví se pouze lokální vlastní tvary. Výchozí hodnota počátečního předpětí pro emin je ve většině případů vhodná.