Настройка модального анализа ( MOS ) задает правила, по которым рассчитываются собственные числа. Предустановлены два стандартных типа расчета. Вы можете изменить эти типы или создать дополнительные настройки модального анализа в любое время.
Основное
Вкладка « Основные » управляет настройками, необходимыми для модального анализа, а также некоторые другие элементармые параметры расчета. Программы RFEM и RSTAB предоставляют различные возможности для выбора метода собственных чисел.
метод собственных чисел
В данном разделе можно задать, какой метод будет использоваться для анализа проблемы собственных чисел и сколько собственных форм будет определено.
Метод определения количества форм
В списке можно выбрать один из трех вариантов.
- Заданный пользователем
Пользовательский метод позволяет указать количество наименьших форм для расчета. Можно задать до 9 999 форм колебаний. В дополнение к этому пределу, модель также представляет ограничение на количество возможных форм колебаний: Она соответствует степеням свободы, которые получаются в результате количества точек свободных масс, умноженных на количество направлений, в которых действуют массы.
- Автоматически, чтобы достичь коэффициентов эффективных модальных масс
Программа определяет столько собственных форм, сколько необходимо, пока не будет достигнут заданный коэффициент модальных масс. Для заданных поступательных направлений (X, Y, Z) анализируются коэффициенты эффективных модальных масс.
- Автоматически, чтобы достичь максимальной собственной частоты
Программа определяет столько собственных форм, сколько необходимо для достижения заданной собственной частоты.
Метод решения проблем собственных чисел (для RFEM)
В списке доступны три метода для решения проблемы собственных чисел. Если вы установили автоматический метод определения количества собственных чисел, будет доступен только один метод решения.
Более подробная информация об отдельных методах расчета находится в статьях Бате [1] и Natke [2]].
- Ланцош
Метод Ланцоша подходит в качестве итерационного метода для нахождения наименьших собственных значений и соответствующих собственных форм у больших моделей. В большинстве случаев данный алгоритм позволяет достичь быстрой сходимости. Можно рассчитать до n –1 форм колебаний ( n : степени свободы модели с массой).
Вводное описание затем можно найти на en.wikipedia.org/wiki/Lanczos_algorithm.
- Корень характеристического полинома
В данном методе аналитическое решение задачи собственных чисел выполняется прямым методом. Основным преимуществом этого метода является точность высших собственных значений и возможность определения всех собственных значений модели. Однако у больших моделей этот метод может быть довольно трудоемким.
Вводное описание затем можно найти на en.wikipedia.org/wiki/Characterist_polynomial.
- Итерация субпространства
В данном методе все собственные значения определяются за один шаг. В данном случае спектр матрицы жесткости оказывает сильное влияние на продолжительность расчета. Таким образом, этот метод рекомендуется только для больших моделей КЭ, если вы хотите рассчитать несколько собственных чисел. Рабочая память ограничивает количество собственных значений, которые могут быть определены в разумный отрезок времени.
Вводное описание находится на en.wikipedia.org/wiki/Krylov_subspace.
Метод решения проблем собственных чисел (для RSTAB)
В списке доступны два метода для решения проблемы собственных чисел. В случае, если вы выбрали один из автоматических методов для определения количества собственных чисел, будет в программе доступен только один метод решения.
Для получения более подробной информации об отдельных методах, см.
- Итерация субпространства
В данном методе все собственные значения определяются за один шаг. В данном случае спектр матрицы жесткости оказывает сильное влияние на продолжительность расчета. Таким образом, этот метод рекомендуется только для больших моделей КЭ, если вы хотите рассчитать несколько собственных чисел. Рабочая память ограничивает количество собственных значений, которые могут быть определены в разумный отрезок времени.
Вводное описание находится на en.wikipedia.org/wiki/Krylov_subspace.
- Обратный степенной метод со сдвигом
Этот метод основан на предположениях для собственных векторов форм колебаний, которые в ходе расчета итерационно приближены к сходящемуся решению. Преимуществом данного метода является короткое время расчета благодаря быстрой сходимости. «Сдвиг» означает, что данный метод можно также использовать для нахождения всех результатов между наибольшим и наименьшим собственным значением данной матрицы.
Вводное описание метода можно найти на en.wikipedia.org/wiki/Inverse_iteration.
Параметры матрицы масс
В этом разделе диалога можно задать, какая матрица масс будет использоваться, и вдоль или вокруг каких осей массы должны действовать в модальном анализе.
тип матрицы масс
Для выбора в перечне доступны три типа матрицы масс.
- Диагональ
В случае диагональной матрицы масс M, предполагается, что массы сосредоточены в узлах КЭ. Вводом матрици являются сосредоточенные массы в поступательных направлениях X, Y и Z, а также направления вращения вокруг глобальных осей X (φX ), Y (φY ) и Z (φZ ). Необходимо различать следующие два случая:
– Диагональная матрица только с поступательными степенями свободы: Если для диагональной матрицы активированы только поступательные направления, то диагональная матрица приведет к:
– Диагональная матрица с поступательными и поворотными степенями свободы: При активации поступательных направлений и вращательных направлений диагональная матрица получается:
|
m |
Масса |
|
IX, IY, IZ |
Моменты инерции массы (RFEM 6) |
- Согласованная
Соответствующая матрица масс - это полная матрица масс конечных элементов. Таким образом, массы не концентрируются на узле КЭ. Вместо этого функции формы используются для более реалистичного распределения масс в конечных элементах. С помощью данной матрицы масс учитываются недиагональные элементы в матрице, таким образом учитывается вращение масс. Соответствующая матрица масс имеет следующую структуру (функции формы не учитываются для простоты):
- Единица измерения
Единичная матрица перезаписывает все ранее заданные массы. Данная матрица представляет собой последовательную матрицу, в которой все диагональные элементы равны 1 кг. Масса установлена на 1 в каждом узле КЭ. Учитываются перемещения и повороты масс. Данный математический подход следует применять только для численного анализа.
Более подробную информацию о типах матриц и особенно о применении единичной матрицы можно найти в работе по Барту/Rustler [3].
В направлении/Вокруг оси
Шесть флажков контролируют, в каком направлении или вокруг каких осей действуют массы при нахождении собственных чисел. Массы могут действовать в глобальных направлениях перемещения X, Y или Z, а также вращаться вокруг осей X, Y и Z. Установите соответствующие флажки. Для расчета собственных чисел необходимо активировать хотя бы одно направление или ось.
Опции
В последнем разделе диалога вкладки «Основные данные» находится важная опция настройки для модального анализа.
Найти формы за пределами частоты
Если отдельные стержни или поверхности имеют в модели очень низкую собственную частоту, то они сначала возникают в качестве местных собственных форм. Если вы установите флажок, будут рассчитаны только собственные числа выше определенного значения «f» собственной частоты. Таким образом, можно уменьшить количество результатов и ограничить их собственными числами, соответствующими общей модели.
Предпочтения
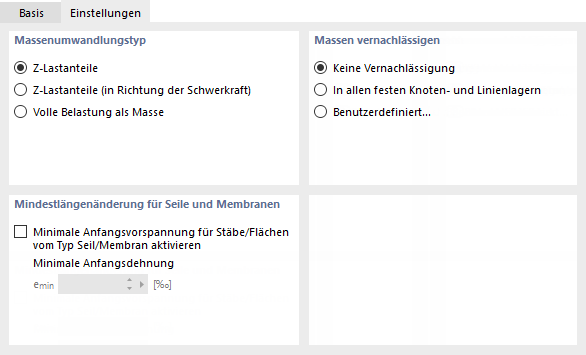
Вкладка Параметры управляет дополнительными настройками, необходимыми для модального анализа, а также задаются параметрами элементарного расчета.
Тип преобразования массы
Этот раздел диалога управляет импортом масс для модального анализа. По умолчанию учитываются только «'Z-компоненты нагрузок». Это относится к компонентам нагрузки, действующим в обоих направлениях оси Z - положительной и отрицательной.
С опцией «Компоненты нагрузки Z (в направлении гравитации)» программа применяется только те компоненты нагрузки, которые эффективны в направлении силы тяжести. Сила тяжести определяется ориентацией общей оси Z (см. раздел {%://#/ru/skachat-i-info/dokumenty/rukovodstva-online/rfem-6/000369#global-axes Ориентация оси]] руководства RFEM): Она действует в направлении общей оси Z, если та направлена вниз. Если общая ось Z ориентирована вверх, это имеет противоположный эффект.
Чтобы импортировать все нагрузки и применить все компоненты в качестве масс, выберите возможность «Полные нагрузки как масса».
Не учитывать массы
Модальный анализ учитывает все массы, заданные в модели. В данном разделе диалога можно пренебречь массой частей модели, например, массой во всех неподвижных узловых и линейных опорах. Вы также можете сделать выбор пользовательского объекта.
При выборе возможности «Пользовательский» появляется дополнительная вкладка «Пренебречь массы». Здесь можно указать объекты без масс.
Список объектов (узлы, линии, стержни и т.д.) можно создать напрямую, используя номера объектов. В качестве альтернативы можно
![]() в поле ввода «Список объектов», чтобы выбрать объекты графически. Нажмите на
в поле ввода «Список объектов», чтобы выбрать объекты графически. Нажмите на
![]() чтобы предустановить только неподвижные опоры.
чтобы предустановить только неподвижные опоры.
Используйте флажки для направлений перемещения uX, uY, и uZ, а также для поворотов φX, φY и φZ, чтобы задать, в каком направлении следует пренебрегать массами.
Тем не менее, жесткость объектов, массами которых пренебрегают, учитывается в матрице. Если вы хотите пренебречь жесткостью этих объектов, то можно использовать модификацию конструкции для настройки жесткости по отдельности. Также можно деактивировать объекты для расчета (см. главу № в руководстве пользователя RFEM. image@028432#
Минимальная осевая деформация для канатов и мембран
Правильный ввод стержни канатов и мембранные поверхности требует минимального изменения длины. Если предел установлен слишком низким, то достигнутые собственные значения не будут реалистичными и будут определяться только местные собственные формы. Значение по умолчанию начального предварительного напряжения для emin в большинстве случаев подходит.