Ustawienie analizy modalnej ( MOS ) określa zasady, zgodnie z którymi obliczane są wartości własne. Domyślnie ustawione są dwa standardowe typy analizy. Te typy ustawień można w dowolnym momencie dostosować lub utworzyć dodatkowe ustawienia dla analizy modalnej.
Główne
Zakładka Główne umożliwia zarządzanie ustawieniami wymaganymi dla analizy modalnej oraz niektórych innych podstawowych parametrów obliczeniowych. Programy RFEM i RSTAB oferują różne opcje wyboru metody wartości własnych.
metoda wartości własnych
W tej sekcji można zdefiniować, która metoda zostanie użyta do analizy problemu wartości własnej i ile kształtów drgań zostanie określonych.
Metoda wyznaczania liczby modów
Do wyboru są trzy opcje z listy.
- Zdefiniowana przez użytkownika
Metoda zdefiniowana przez użytkownika umożliwia określenie liczby najmniejszych postaci, które mają zostać obliczone. Można zdefiniować do 9999 kształtów drgań. Oprócz tego ograniczenia model ogranicza również liczbę możliwych kształtów drgań własnych: Odpowiada ona stopniom swobody wynikającym z liczby punktów o swobodnych masach pomnożonych przez liczbę kierunków, w których działają masy.
- Automatycznie, aby osiągnąć współczynniki efektywnej masy modalnej
Program określa niezbędną liczbę postaci własnych, aż do osiągnięcia określonego modalnego współczynnika masy. Dla określonych kierunków translacyjnych (X, Y, Z) analizowane są efektywne współczynniki masy modalnej.
- Automatycznie, aby osiągnąć częstotliwość drgań własnych
Program określa niezbędną liczbę postaci własnych, aż do osiągnięcia określonej częstotliwości drgań własnych.
Metoda rozwiązywania problemu wartości własnych (RFEM)
Na liście dostępne są trzy metody rozwiązywania problemu wartości własnych. Jeżeli aktywowano automatyczną metodę określania liczby wartości własnych, dostępna jest tylko jedna metoda rozwiązywania.
Więcej informacji na temat poszczególnych metod można znaleźć w sekcji Bathe [1] and Natke [2].
- Lanczos
Metoda Lanczosa może być stosowana jako metoda iteracyjna do określania najniższych wartości własnych i odpowiadających im postaci drgań w dużych modelach. W większości przypadków algorytm ten pozwala na uzyskanie szybkiej zbieżności. Możliwe jest obliczenie do n–1 postaci drgań ( n : stopni swobody modelu z masą).
Opis wprowadzający można znaleźć na stronie pl.wikipedia.org/wiki/Lanczos_algorithm.
- Pierwiastek wielomianu charakterystycznego
Dzięki tej metodzie analityczne rozwiązanie problemu wartości własnych jest przeprowadzane metodą bezpośrednią. Główną zaletą tej metody jest dokładność przy wyznaczaniu wyższych wartości własnych oraz możliwość wyznaczania wszystkich wartości własnych modelu. W przypadku większych modeli metoda ta może być czasochłonna.
Opis wprowadzający można znaleźć na stronie pl.wikipedia.org/wiki/Characteristic_polynomial.
- Iteracja podprzestrzeni
Przy użyciu tej metody wszystkie wartości własne są określane w jednym kroku. W takim przypadku spektrum macierzy sztywności ma duży wpływ na czas trwania obliczeń. Dlatego w przypadku dużych modeli elementów skończonych ta metoda jest zalecana tylko w przypadku obliczania kilku wartości własnych. Pamięć robocza ogranicza liczbę wartości własnych, które można określić w rozsądnym czasie.
Opis wprowadzający można znaleźć na stronie pl.wikipedia.org/wiki/Krylov_subspace.
Metoda rozwiązywania problemu wartości własnych (dla RSTAB)
Na liście dostępne są dwie metody rozwiązania problemu wartości własnej. W przypadku wybrania jednej z automatycznych metod określania liczby wartości własnych, dostępna jest tylko jedna metoda rozwiązywania.
Więcej informacji na temat poszczególnych metod można znaleźć w sekcji Bathe [1].
- Iteracja podprzestrzeni
Przy użyciu tej metody wszystkie wartości własne są określane w jednym kroku. W takim przypadku spektrum macierzy sztywności ma duży wpływ na czas trwania obliczeń. Dlatego w przypadku dużych modeli elementów skończonych ta metoda jest zalecana tylko w przypadku obliczania kilku wartości własnych. Pamięć robocza ogranicza liczbę wartości własnych, które można określić w rozsądnym czasie.
Opis wprowadzający można znaleźć na stronie pl.wikipedia.org/wiki/Krylov_subspace.
- Metoda Powera z przesuniętą odwrotnością
Metoda ta opiera się na założeniach dotyczących wektorów własnych postaci drgań, które podczas obliczeń są iteracyjnie przybliżane do rozwiązania zbieżnego. Zaletą tej metody jest krótki czas obliczeń ze względu na szybką zbieżność. "Przesunięcie" oznacza, że ta metoda może być również użyta do określenia wszystkich wyników pomiędzy największą i najmniejszą wartością własną danej macierzy.
Opis wprowadzający można znaleźć na stronie pl.wikipedia.org/wiki/Inverse_iteration.
Ustawienia macierzy mas
W tej sekcji można określić, która macierz mas zostanie zastosowana oraz w jakich osiach lub względem których osi mają działać masy w analizie modalnej.
typ macierzy mas
Na liście dostępne są trzy typy macierzy mas.
- Diagonalna
W przypadku diagonalnej macierzy mas M przyjmuje się, że masy są skupione w węzłach ES. Dane wejściowe do macierzy stanowią masy skupione w kierunkach translacyjnych X, Y i Z oraz w kierunkach obrotu względem globalnych osi X (φX ), Y (Y ) i Z (φZ ). Należy rozróżnić dwa przypadki:
– Macierz diagonalna z tylko translacyjnymi stopniami swobody: Jeżeli dla macierzy diagonalnej aktywowane są tylko kierunki translacyjne, wynik macierzy diagonalnej:
– Macierz diagonalna z translacyjnymi i rotacyjnymi stopniami swobody: Jeżeli aktywowane są kierunki translacyjne oraz kierunki obrotu, macierz diagonalna daje:
|
m |
Masa |
|
IX, IY, IZ |
Momenty bezwładności masy (RFEM 6) |
- Konsystentna
Spójna macierz mas jest pełną macierzą mas elementów skończonych. Dzięki temu masy nie są skoncentrowane w węźle ES. Zamiast tego, funkcje kształtu służą do bardziej realistycznego rozmieszczenia mas w elementach skończonych. Przy użyciu tej macierzy mas uwzględniane są dane niebędące przekątną, dzięki czemu zazwyczaj uwzględniany jest obrót mas. Spójna macierz mas ma następującą strukturę (dla uproszczenia pominięto funkcje kształtu):
- Jednostka
Macierz jednostek nadpisuje wszystkie zdefiniowane wcześniej masy. Jest to macierz spójna, w której wszystkie elementy na przekątnej mają wartość 1 kg. Masa jest ustawiona na 1 w każdym węźle ES. Uwzględniane są przesunięcia i obroty mas. To matematyczne podejście powinno być stosowane tylko do analiz numerycznych.
Więcej informacji na temat typów macierzy, a zwłaszcza na temat stosowania macierzy jednostek, można znaleźć w Barth/Rustler [3].
W kierunku/względem osi
Sześć pól wyboru określa, w którym kierunku lub wokół jakich osi działają masy podczas określania wartości własnych. Masy mogą działać w globalnych kierunkach przemieszczeń X, Y lub Z i obracać się wokół osi X, Y i Z. Należy zaznaczyć odpowiednie pola wyboru. W celu obliczenia wartości własnych należy aktywować co najmniej jeden kierunek lub oś.
Opcje
Ostatnia sekcja okna dialogowego w zakładce "Główne" zapewnia ważną opcję ustawień dla analizy modalnej.
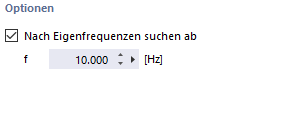
Znajdź wektory własne poza częstotliwością
Jeżeli poszczególne pręty lub powierzchnie w modelu mają bardzo niską częstotliwość drgań własnych, najpierw pojawiają się jako lokalne postacie własne. W przypadku zaznaczenia pola wyboru zostaną obliczone tylko wartości własne powyżej określonej wartości "f" częstotliwości drgań własnych. W ten sposób można zredukować liczbę wyników i ograniczyć ją do wartości własnych, które są istotne dla modelu globalnego.
Ustawienia i opcje
Zakładka Ustawienia umożliwia zarządzanie dalszymi ustawieniami wymaganymi do analizy modalnej oraz podstawowymi parametrami obliczeniowymi.
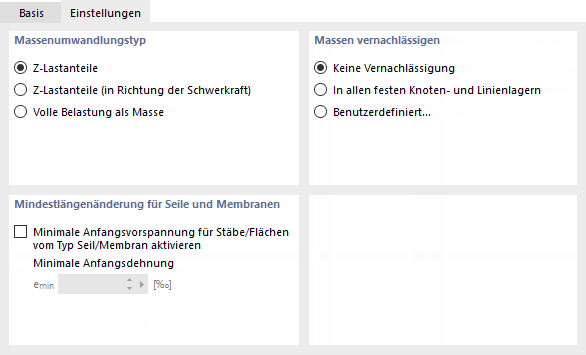
typ konwersji masy
Ta sekcja okna dialogowego kontroluje import mas do analizy modalnej. Domyślnie uwzględniane są tylko "'Składowe obciążeń Z". Dotyczy to składowych obciążenia działających w obu kierunkach osi Z – dodatnim i ujemnym.
Dzięki opcji "Składowe obciążenia Z (w kierunku grawitacji)" program stosuje tylko składowe obciążenia, które działają w kierunku grawitacji. Siła ciężkości jest określana przez orientację globalnej osi Z (patrz rozdział Axis Orientation instrukcji do programu RFEM): Działa on w kierunku globalnej osi Z, jeżeli jest skierowana w dół. Skierowanie globalnej osi Z do góry ma odwrotny skutek
Po wybraniu opcji 'Pełne obciążenia jako masa' wszystkie obciążenia zostają zaimportowane i zastosowane jako masy.
Pomiń masy
W analizie modalnej uwzględniane są wszystkie masy zdefiniowane w modelu. Ta sekcja okna dialogowego zawiera możliwość pominięcia mas części modelu, takich jak masy we wszystkich utwierdzonych podporach węzłowych i liniowych. Można też wybrać obiekty zdefiniowane przez użytkownika.
Po wybraniu opcji "Zdefiniowane przez użytkownika" pojawia się dodatkowa zakładka "Pomiń masy". Tutaj można określić obiekty bez mas.
Listę obiektów (węzłów, linii, prętów itp.) można utworzyć bezpośrednio przy użyciu numerów obiektów. Alternatywnie można zastosować
![]() w polu tekstowym "Listy obiektów", aby wybrać obiekty graficznie. Przycisk
w polu tekstowym "Listy obiektów", aby wybrać obiekty graficznie. Przycisk
![]() aby wstępnie ustawić tylko podpory utwierdzone.
aby wstępnie ustawić tylko podpory utwierdzone.
Za pomocą pól wyboru dla kierunków przemieszczeń uX, uY, i uZ oraz obrotów φX, φY i φZ można określić, w którym kierunku mają zostać pominięte masy.
Sztywność obiektów, których masy są pominięte, jest jednak uwzględniana w macierzy. Jeśli chcesz pominąć sztywność również tych obiektów, można użyć modyfikacji konstrukcji, aby indywidualnie dostosować sztywności. Istnieje również możliwość dezaktywacji obiektów do obliczeń (patrz rozdział (główny instrukcji obsługi programu RFEM).
Minimalne odkształcenie osiowe dla kabli i membran
Prawidłowy wpis kabel pręty i powierzchnie membranowe wymagają minimalnej zmiany długości. Jeżeli wartość graniczna jest ustawiona zbyt nisko, osiągnięte wartości własne nie są realistyczne i określane są tylko lokalne postacie własne. W większości przypadków odpowiednia jest domyślna wartość początkowego naprężenia wstępnego dla emin.