Расчёт стационарного потока можно выбрать на вкладке "Общие" диалогового окна "Параметры моделирования" (см. изображение Параметры моделирования ).
Начальные условия
При активации опции "Использовать потенциальный поток для расчёта начального условия" используется линеаризованная версия уравнений Навье-Стокса для невязкой жидкости для генерации начальных условий.
Расчёт стационарного потока
Вы можете задать "Максимальное количество итераций". По умолчанию, предел составляет 500 итераций. Если расчёт сходится с меньшим количеством итераций, он прекращается. Вы также можете задать "Минимальное количество итераций", которое по умолчанию установлено на 300 итераций (см. изображение Параметры программы ), независимо от того, выполнено ли уже условие сходимости (см. ниже). Максимальное количество полезно для предотвращения бесконечных циклов.
"Критерий сходимости" представляет собой предел остановки для расчёта. Доступны два критерия сходимости; вы можете следовать либо критерию давления, либо критерию силы сопротивления. Выберите один из вариантов в Тип остатка и затем установите целевое значение.
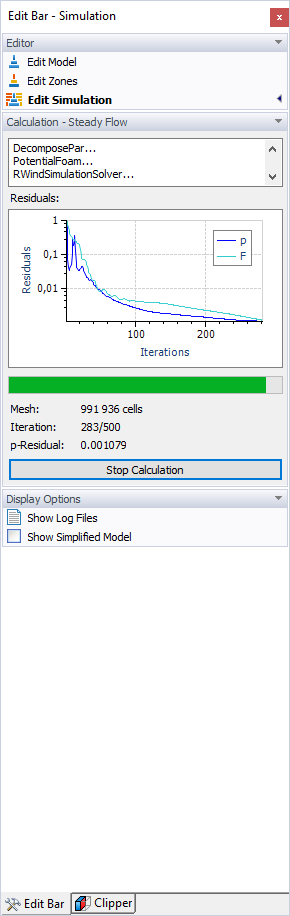
Как только величина остатка падает ниже установленного значения, расчёт прекращается. Диаграмма итераций и остаточной величины (p-остаток для давления) отображается во время расчёта. Она также доступна в результатах моделирования (см. главу Остатки).
Флажок "Использовать численную схему второго порядка" контролирует, какая численная схема используется для дивергенциальных членов (потоков). По умолчанию он не активирован, поэтому расчёт выполняется согласно первому порядку. Если флажок выбран, решение выполняется согласно второму порядку.
Другие опции
Стационарный решатель RWIND 3 не полностью захватывает "колебательные" эффекты, как описано в FAQ 4731. Для численного решения уравнений в частных производных все дифференциальные члены (производные по пространству и времени) должны быть дискретизированы. Вы можете найти больше информации о решателях в документации Алгоритмы и решатели. Существует обширный список дискретизаций ("схем"), каждая из которых имеет особое численное поведение с точки зрения точности, стабильности и сходимости. Для получения дополнительной информации о сходимости смотрите CFD Direct.