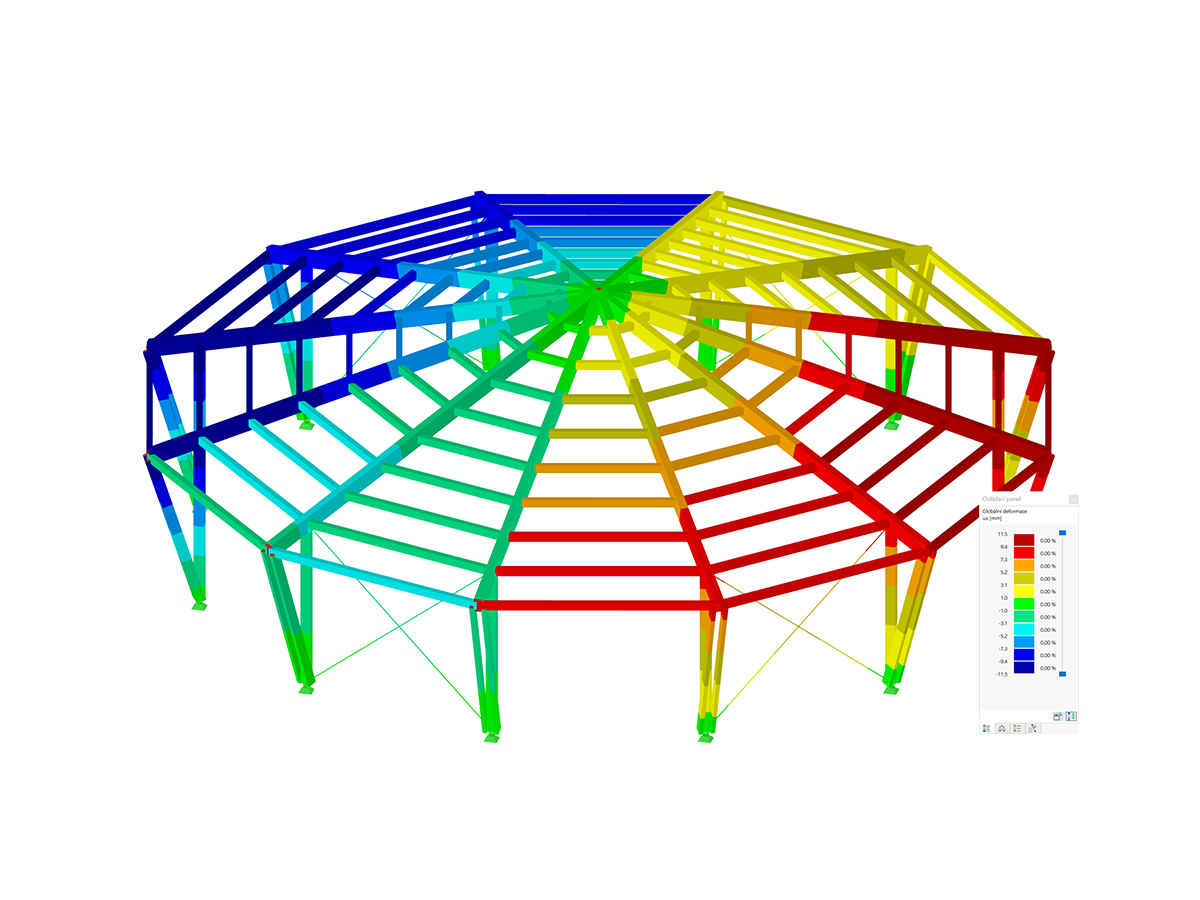
A iteração é um processo repetitivo que se aproxima de um objetivo. In der numerischen Tragwerksanalyse wird diese Methode meist zur Findung einer Lösung von Aufgaben mit nichtlinearen Zusammenhängen genutzt. Solch eine Aufgabenstellungen besteht in der Regel aus einer Gleichung mit nichtlinearen Termen, die von einer Variablen abhängig sind.
Der Iterationsprozess setzt in einem ersten Schritt einen beliebigen Startwert für die unbekannte Variable ein und löst die Terme auf der linken und rechten Seite der Gleichung. Ist die Gleichung nicht erfüllt, wiederholt sich der Prozess mit einem modifizierten Startwert. Dieser iterative Vorgang läuft solange, bis die Gleichung erfüllt ist. In diesem Fall spricht man von einer Konvergenz und der zuletzt eingesetzte Variablenwert ist die Lösung.
Die Genauigkeit dieses Verfahrens hängt von den eingesetzten Variablen ab. Dies bedeutet, dass man zur Findung der exakten Lösung meist sehr viele Iterationen vornehmen muss. Wenn eine Lösung mit reduzierter Genauigkeit ausreichend ist, knüpft man die Konvergenz der Iteration an ein Toleranzkriterium. Dabei wird nur dann eine neue Iteration gestartet, wenn die Differenz zwischen den Termen der linken und rechten Seite der Gleichung größer als ein definiertes Toleranzkriterium ist.
Iterative Prozesse in der Tragwerksanalyse
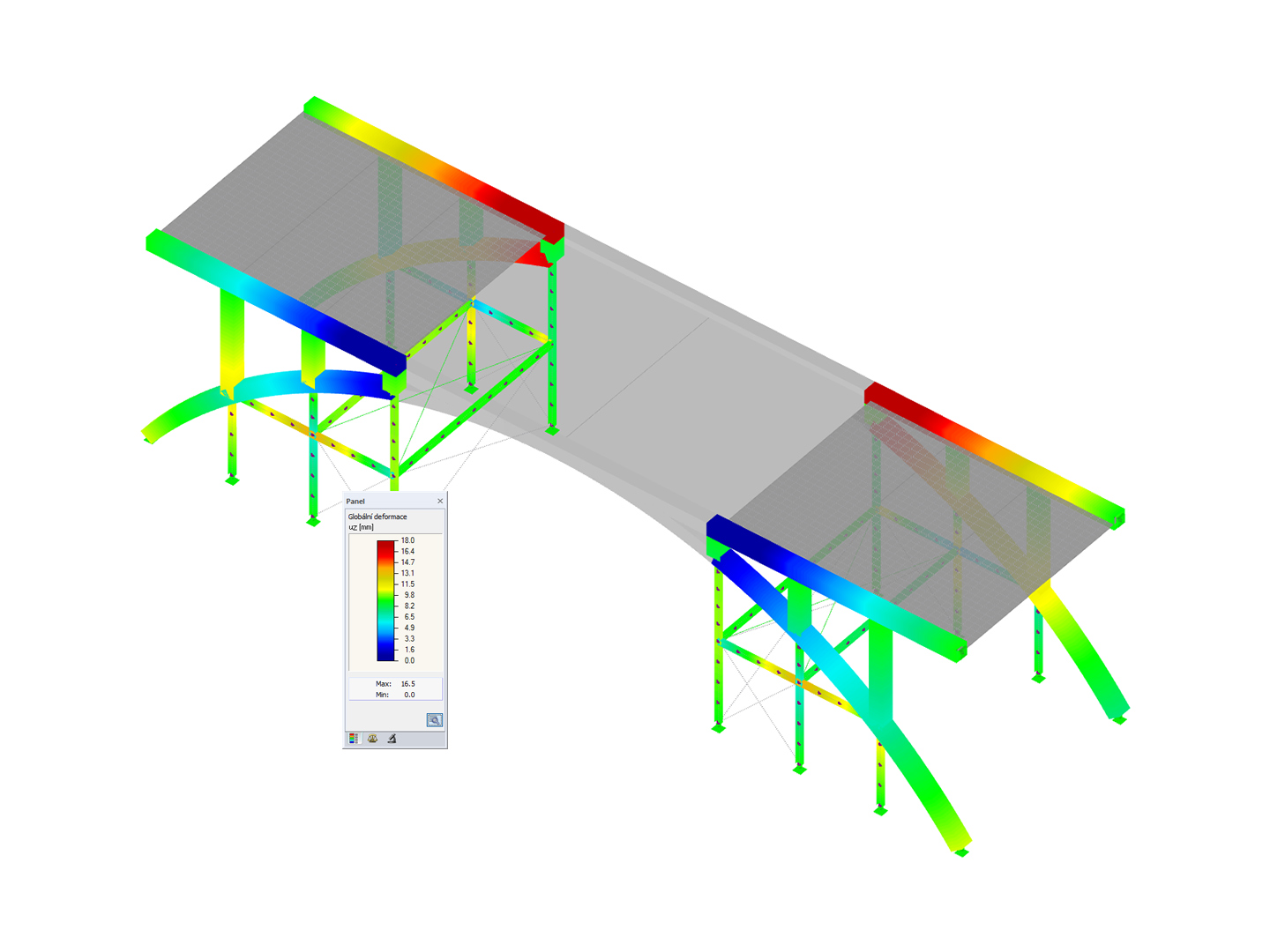
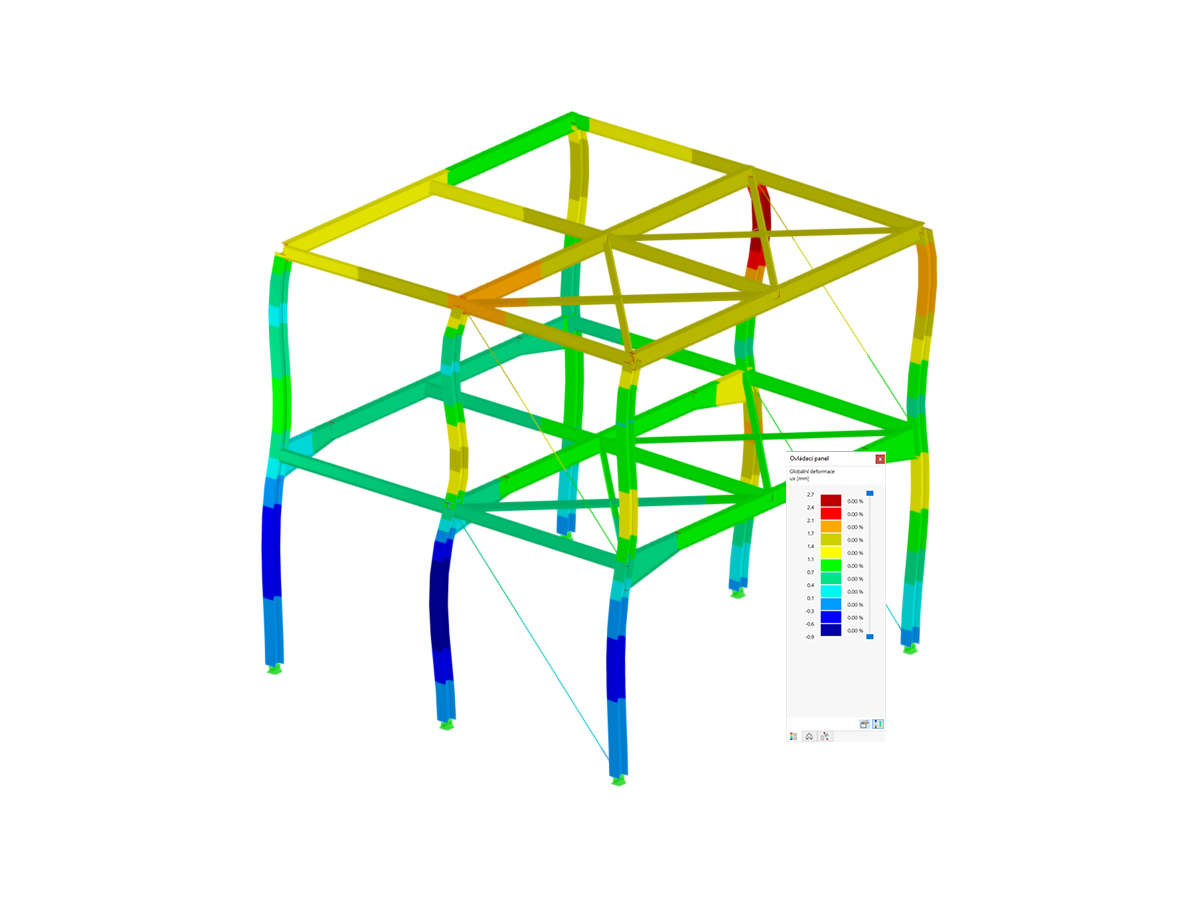
- Ermittlung von Schnittgrößen am verformten System (Theorie II. Ordnung)
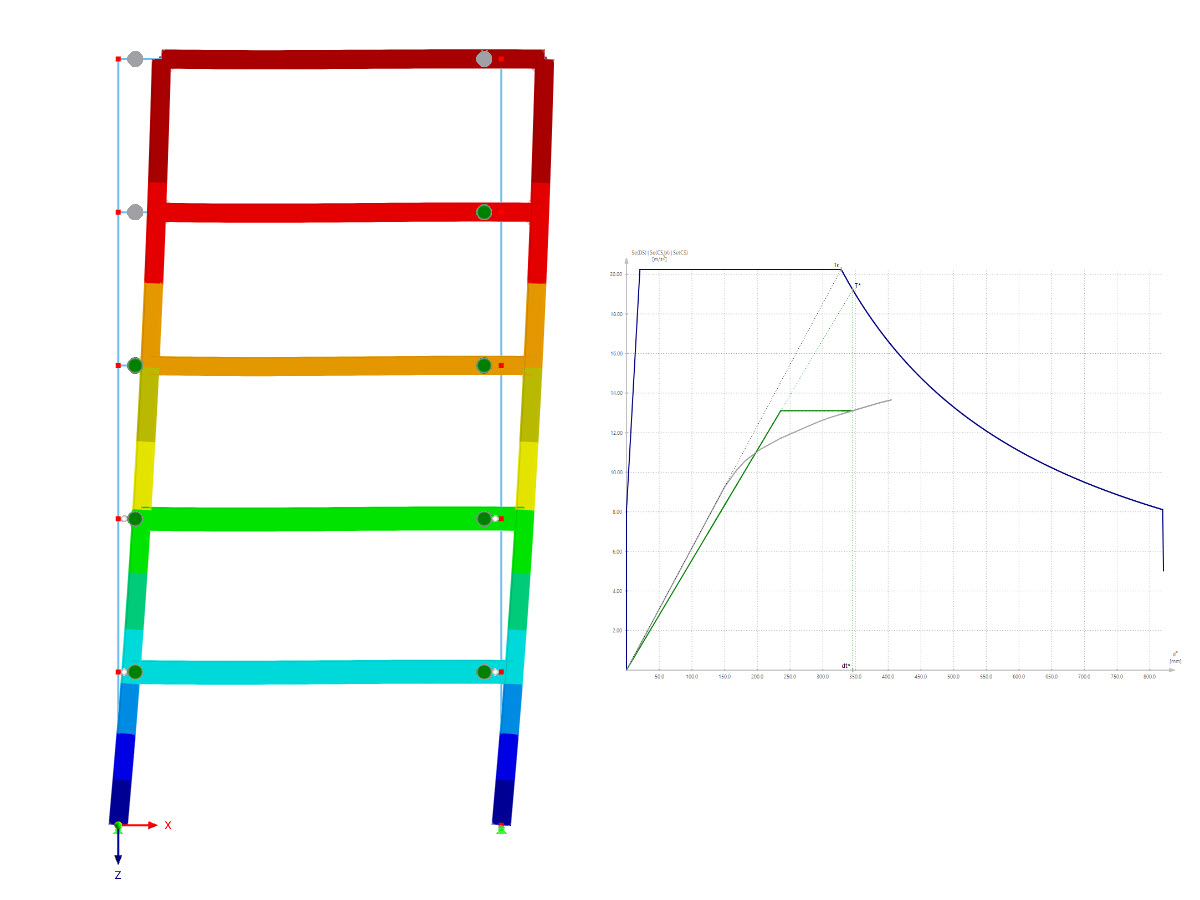
- Simulation von nichtlinearen Materialeigenschaften (Plastizität)
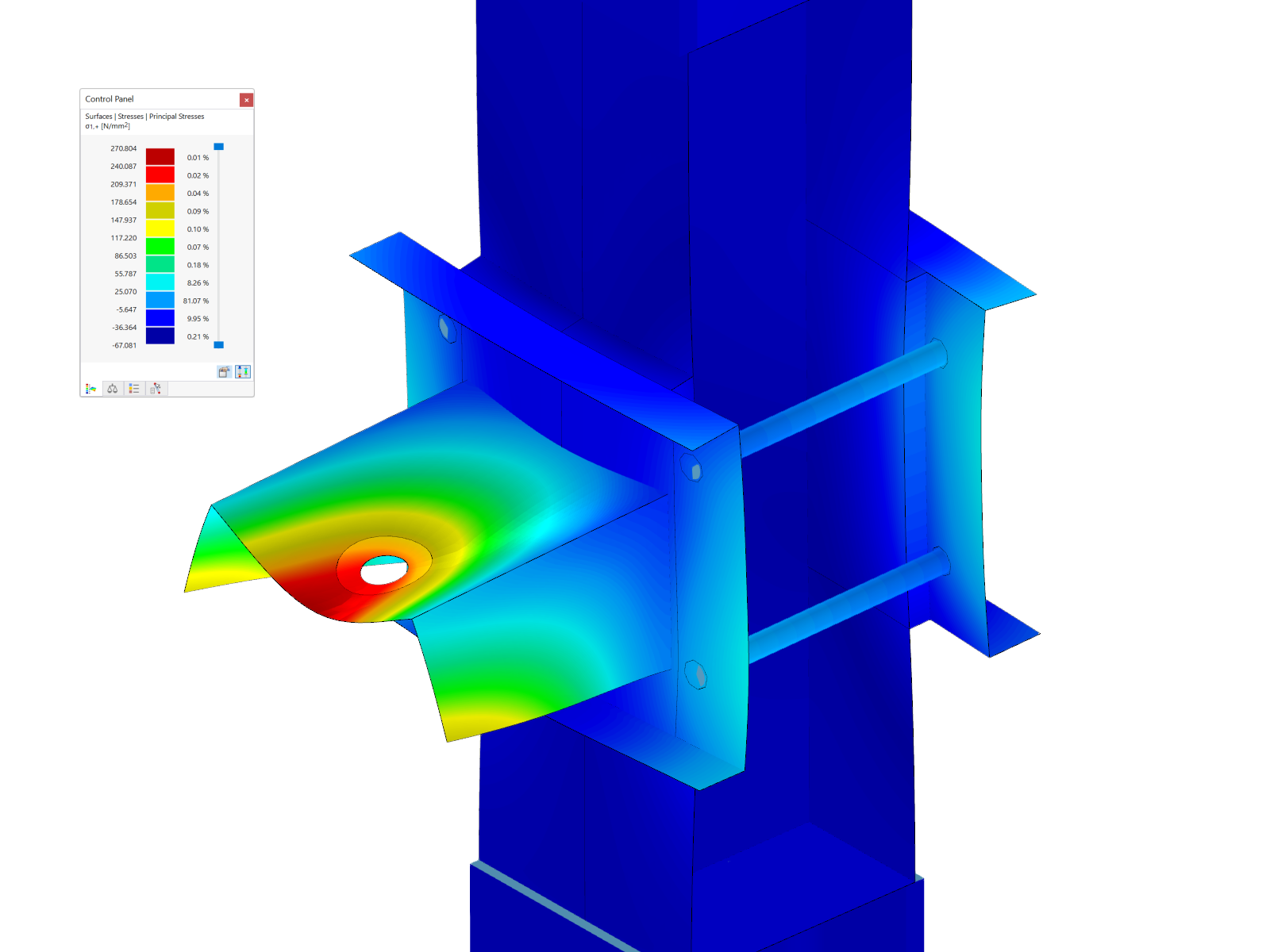
- Ermittlung von Kontaktspannungen zwischen zwei formschlüssig miteinander verbundenen Körpern
Iterationen in RFEM und RSTAB
In RFEM 5 und RSTAB 8 sind die Kriterien und maximalen Iterationen für nichtlineare Berechnungen unter "Berechnung" → "Berechnungsparameter" im Register "Globale Berechnungsparameter" organisiert.
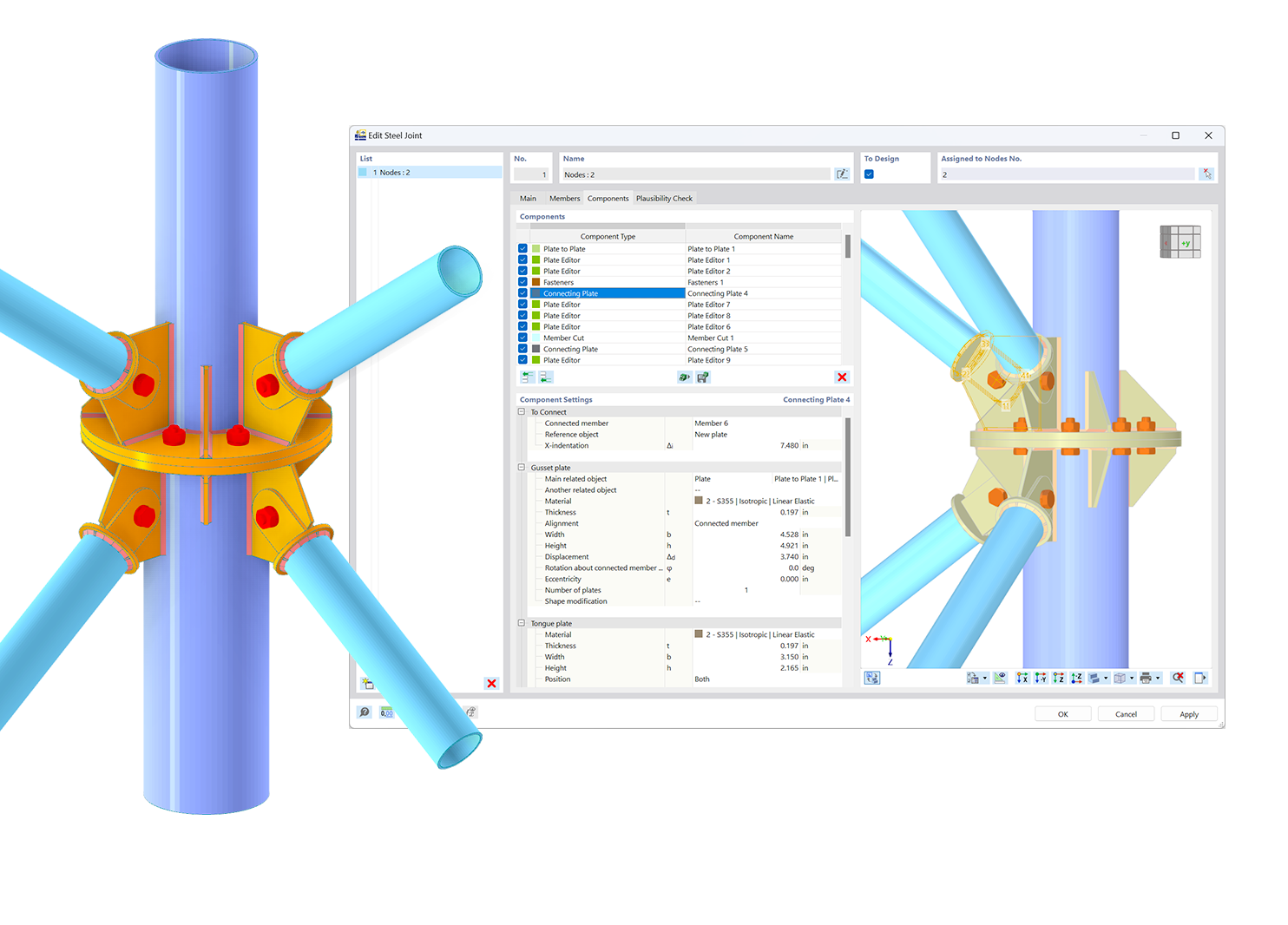
In RFEM 6 und RSTAB 9 werden die Parameter für die Iterationen bei den Statikanalyse-Einstellungen verwaltet.




.png?mw=600&hash=49b6a289915d28aa461360f7308b092631b1446e)