Die ideale Federsteifigkeit ist laut George Winter diejenige, welche mindestens nötig ist, um in Bezug auf die Verzweigungslast des Hauptstabes das seitliche Ausknicken dieses vollständig zu verhindern und dementsprechend wie ein vollwertiges Auflager zu wirken. Winter spricht hier von "Full Bracing". An der Stelle dieser Stützfeder soll demnach der Nulldurchgang der Knicklinie liegen, sodass die Knicklinie selbst zwei- oder mehrwellig anstatt einwellig ist.
Im Winter-Modell wird ein ideal gerader, beidseitig gelenkig gelagerter Druckstab betrachtet, welcher in der Mitte durch eine Stützfeder gehalten ist. Zur Ermittlung der idealen Federsteifigkeit entwickelte Winter das in Bild 01 dargestellte idealisierte Modell.
Das fiktive Gelenk wird mit der Annahme eines Wendepunktes in der Biegeknicklinie bei gleichen Stützweiten begründet. Wird als Drucknormalkraft die Verzweigungslast Pe angesetzt und der Stab im Bereich der Stützfeder um das Maß w verschoben, ergibt sich nach Freischneiden am fiktiven Gelenk und Aufstellung des Momentengleichgewichts die ideale Federsteifigkeit Cideal.
|
Cideal |
Ideale Federsteifigkeit |
|
Pe |
Verzweigungslast |
|
L |
Stützweite zwischen Auflager und Stützfeder |
Aus diesem Zusammenhang zwischen Federsteifigkeit und Verzweigungslast ergibt sich analog die in Bild 02 dargestellte Funktion. Demnach tritt bei Federsteifigkeiten kleiner als Cideal eine Knickfigur mit seitlicher Verschiebung im Bereich der Stützfeder auf.
Die Verzweigungslast Pe kann mit den Zusatzmodulen RSKNICK und RF-STABIL oder per Hand wie folgt ermittelt werden.
|
Pe |
Verzweigungslast |
|
E |
Elastizitätsmodul |
|
I |
Flächenträgheitsmoment |
|
L |
Stützweite zwischen Auflager und Stützfeder |
Ermittlung der idealen Federsteifigkeit anhand eines Beispiels
Im Modell (Bild 03) ist ein beidseitig gelenkig gelagerter Druckstab (IPE 400) mit den Parametern E = 21.000 kN/cm², Iz = 1.318 cm4 und L = 5 m mittig durch eine Stützfeder gehalten.
Es ergibt sich eine Verzweigungslast Pe von 1.089 kN, woraus eine ideale Federsteifigkeit Cideal für die mittig am Stab definierte Stützfeder von 436 kN/m resultiert.
Ermittlung der Stabilisierungskraft in der Stützfeder am Beispiel eines Knickstabes mit Imperfektion
Nachdem in Ergänzung zu den oben genannten theoretischen Überlegungen Traglastversuche an Knickstützen durchgeführt wurden, wurde festgestellt, dass die theoretisch ideale Federsteifigkeit bei Stützen mit geometrischen Imperfektionen nicht ausreicht.
Demnach wird die Verformung w aus Bild 01 durch die Vorverformung w0 zu wges ergänzt.
wges = w + w0
Nach Aufstellung des Momentengleichgewichts um das fiktive Gelenk (Bild 01) ergibt sich:
P ⋅ (w + w0) = C ⋅ w ⋅ L / 2
Daraus ergibt sich:
|
wges |
Gesamtverformung aus Knickauslenkung und Vorkrümmung |
|
w0 |
Vorverformung aus Vorkrümmung aufgrund geometrischer Imperfektion |
|
P |
Vorhandene Drucknormalkraft im Knickstab |
|
C |
Federsteifigkeit der seitlichen Stützfeder |
|
L |
Stützweite zwischen Auflager und Stützfeder |
Und für Cideal = 2 ⋅ Pe / L:
|
wges |
Gesamtverformung aus Knickauslenkung und Vorkrümmung |
|
w0 |
Vorverformung aus Vorkrümmung aufgrund geometrischer Imperfektion |
|
P |
Vorhandene Drucknormalkraft im Knickstab |
|
Pe |
Verzweigungslast im Knickstab |
Aus diesen Gleichungen ergibt sich die Stabilisierungskraft Fc:
|
Fc |
Seitliche Stabilisierungskraft |
|
C |
Federsteifigkeit der seitlichen Stützung |
|
w |
Seitliche Auslenkung des Knickstabes in der Mitte |
|
P |
Drucknormalkraft im Knickstab |
|
L |
Stützweite zwischen Auflager und Stützfeder |
|
w0 |
Vorverformung aus Vorkrümmung aufgrund geometrischer Imperfektion |
|
Pe |
Verzweigungslast des Knickstabes |
Aus folgenden Parametern kann somit die Stabilisierungskraft Fc ermittelt werden:
- Vorhandene Druckkraft P = 500 kN
- Stützweite zwischen Auflager und Stützfeder L = 5,00 m
- Vorkrümmung aus Imperfektion w0 = Lgesamt / 300 = 10 / 300 = 0,0333 m
Verzweigungslast Pe = 1.089 kN
Somit ergibt sich eine Stabilisierungslast Fc = 12,3 kN. RFEM ermittelt 11,7 kN.
Fazit
Zur Überprüfung der Richtigkeit der ermittelten Federsteifigkeit dient ein Blick in die Ergebnisse aus RF-STABIL. Die erste Eigenform ist eine zweiwellige Knicklinie mit Nulldurchgang auf Höhe der Stützfeder, während die zweite Eigenform eine einwellige Knicklinie, gestützt durch die Stützfeder, darstellt (Bild 04). Beide haben annähernd die selbe Verzweigungslast.

















..png?mw=320&hash=bd2e7071b02d74aef6228d22c4b83867d2d7e1a5)























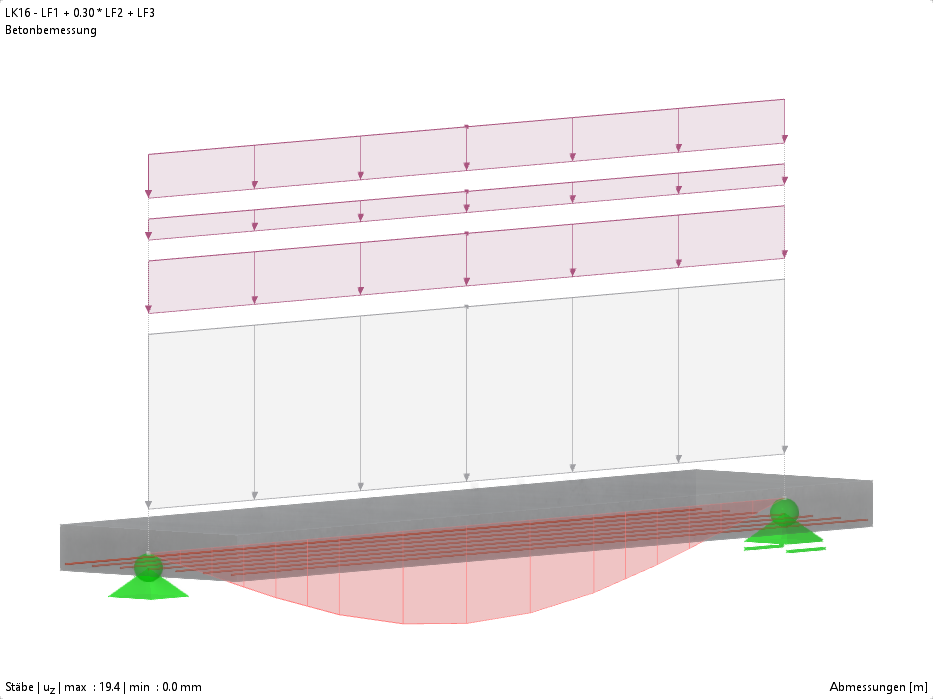















-querkraft-hertha-hurnaus.jpg?mw=350&hash=3306957537863c7a7dc17160e2ced5806b35a7fb)

























.png?mw=600&hash=49b6a289915d28aa461360f7308b092631b1446e)