Come parte del calcolo degli autovalori lineari utilizzando l'add-on Stabilità della struttura, i "Coefficienti di rilevanza modale" (MRF) sono ora mostrati anche per tutte le forme modali e le singole aste oltre ai carichi critici e alle lunghezze efficaci equivalenti determinate da questi carichi. L'MRF descrive qualitativamente la rilevanza di un'asta per una forma modale calcolata. Il calcolo si basa sull'energia di deformazione elastica, che risulta per ogni singola asta ( k ) nella forma modale ( i ). Poiché le forme modali possono essere ridimensionate come richiesto, non vengono considerate energie di deformazione assoluta. Invece, le energie di tutte le singole aste sono messe in relazione l'una con l'altra:
| ui | Forma modale per autovalore i |
| kek | Matrice di rigidezza dell'elemento per l'asta k |
dove
- ui - forma modale per autovalore i
- Kek - Matrice di rigidezza dell'elemento per l'asta k
Un MRF del 100% significa che una singola asta ha la massima rilevanza per la forma modale considerata. Le aste che non hanno un'energia di deformazione significativa in confronto, tuttavia, non sono di alcun interesse per la forma modale in esame.
Come parte della valutazione dell'analisi di stabilità per forma modale, l'MRF può essere utilizzato per distinguere rapidamente e sistematicamente tra forme modali locali e globali. Se più aste singole hanno un MRF significativo per una forma modale (ad esempio maggiore del 20 %), indica un'instabilità dell'intera struttura o di una parte della struttura. Tuttavia, se la somma di tutte le MRF è di circa il 100 % per una forma modale, è prevedibile un fenomeno di stabilità locale (ad esempio instabilità di una singola asta).
Inoltre, l'MRF può essere utilizzato per determinare i carichi critici determinanti e le lunghezze efficaci equivalenti di aste particolari (ad esempio per la verifica di stabilità). Qui, si consiglia la valutazione asta per asta dei risultati dell'analisi. Le forme modali per le quali l'asta ha valori MRF piccoli (ad esempio inferiori al 20 %) possono essere trascurate senza problemi quando si trova la lunghezza efficace critica dell'asta.
Esempio
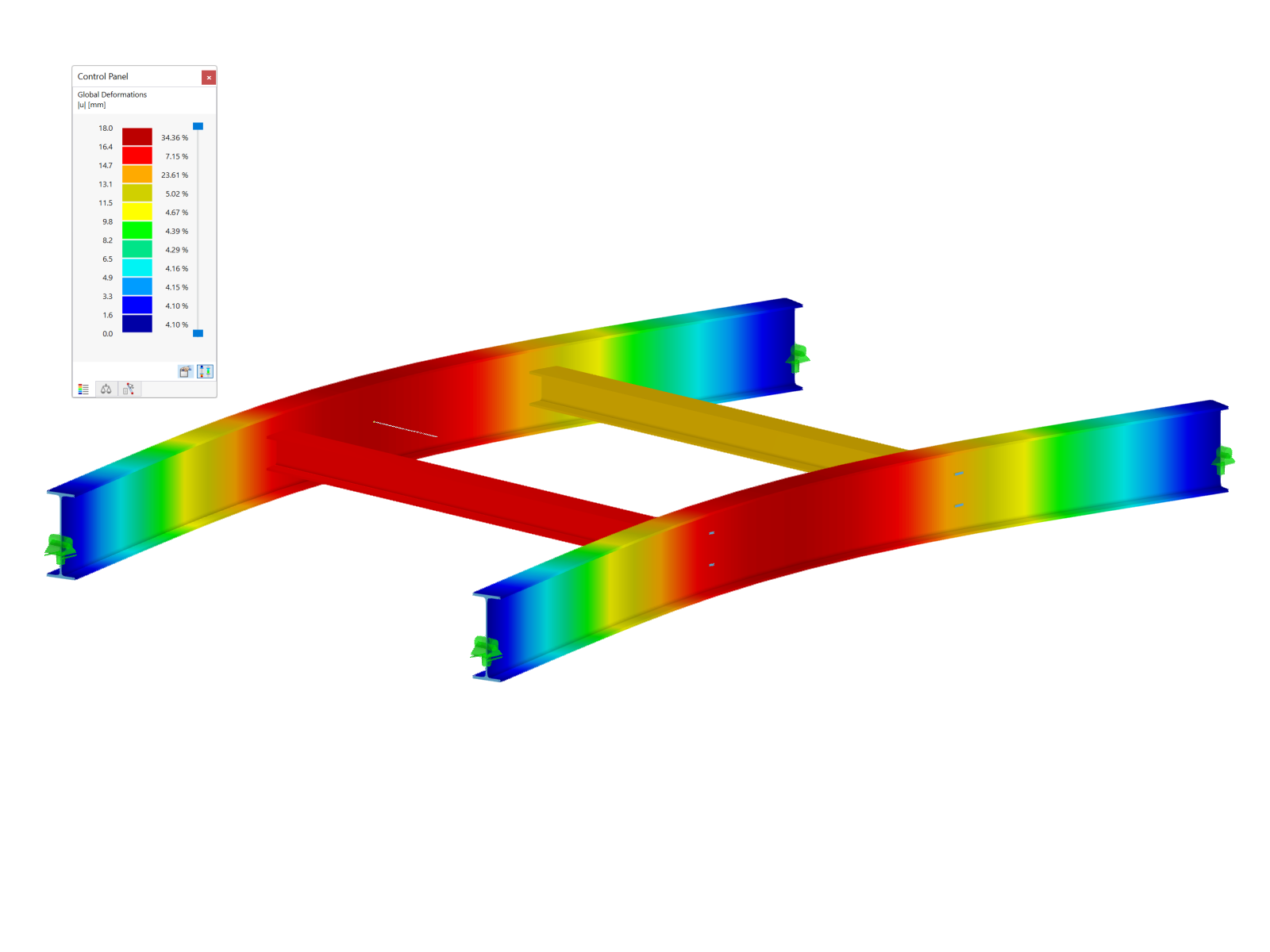
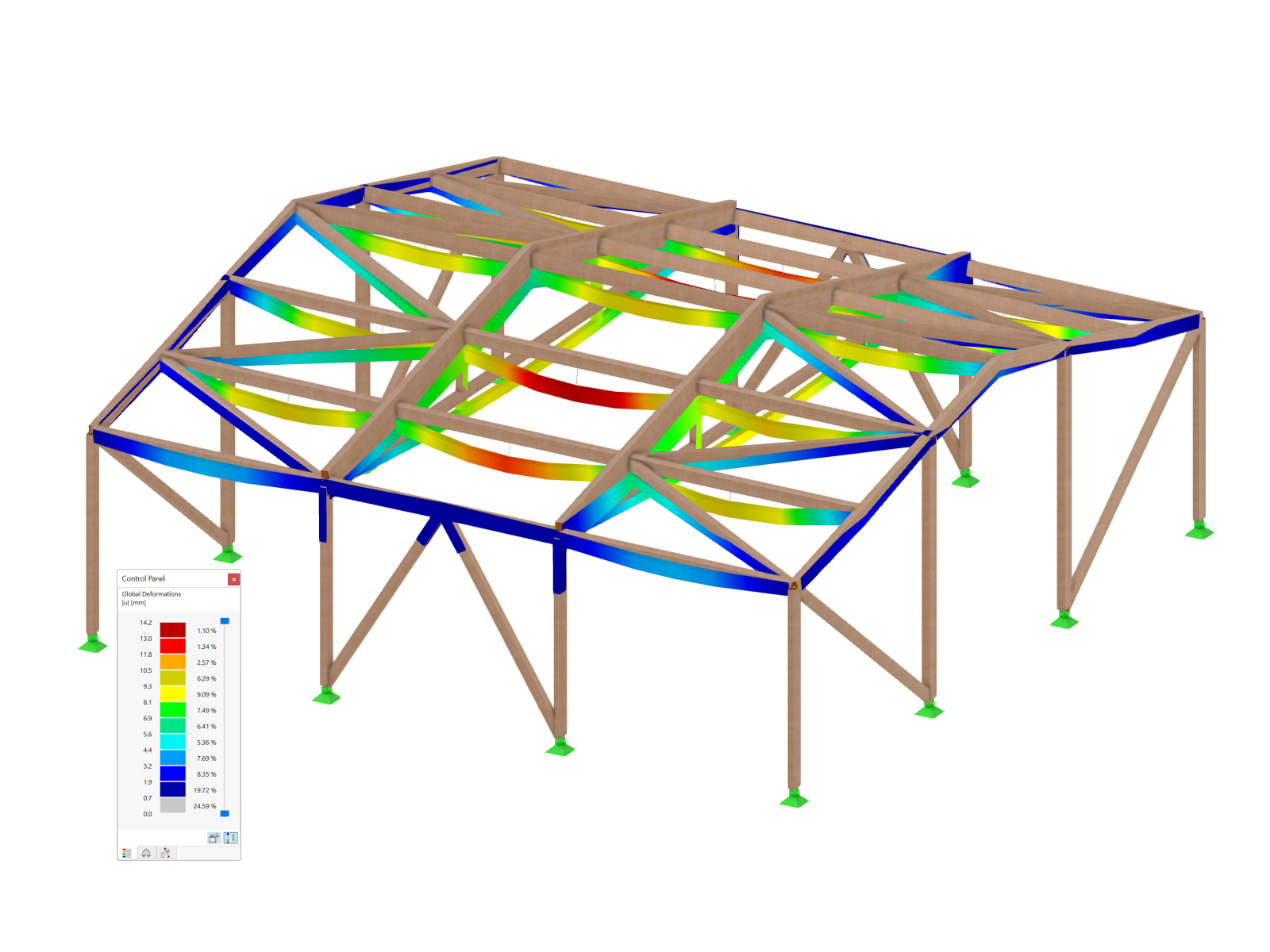
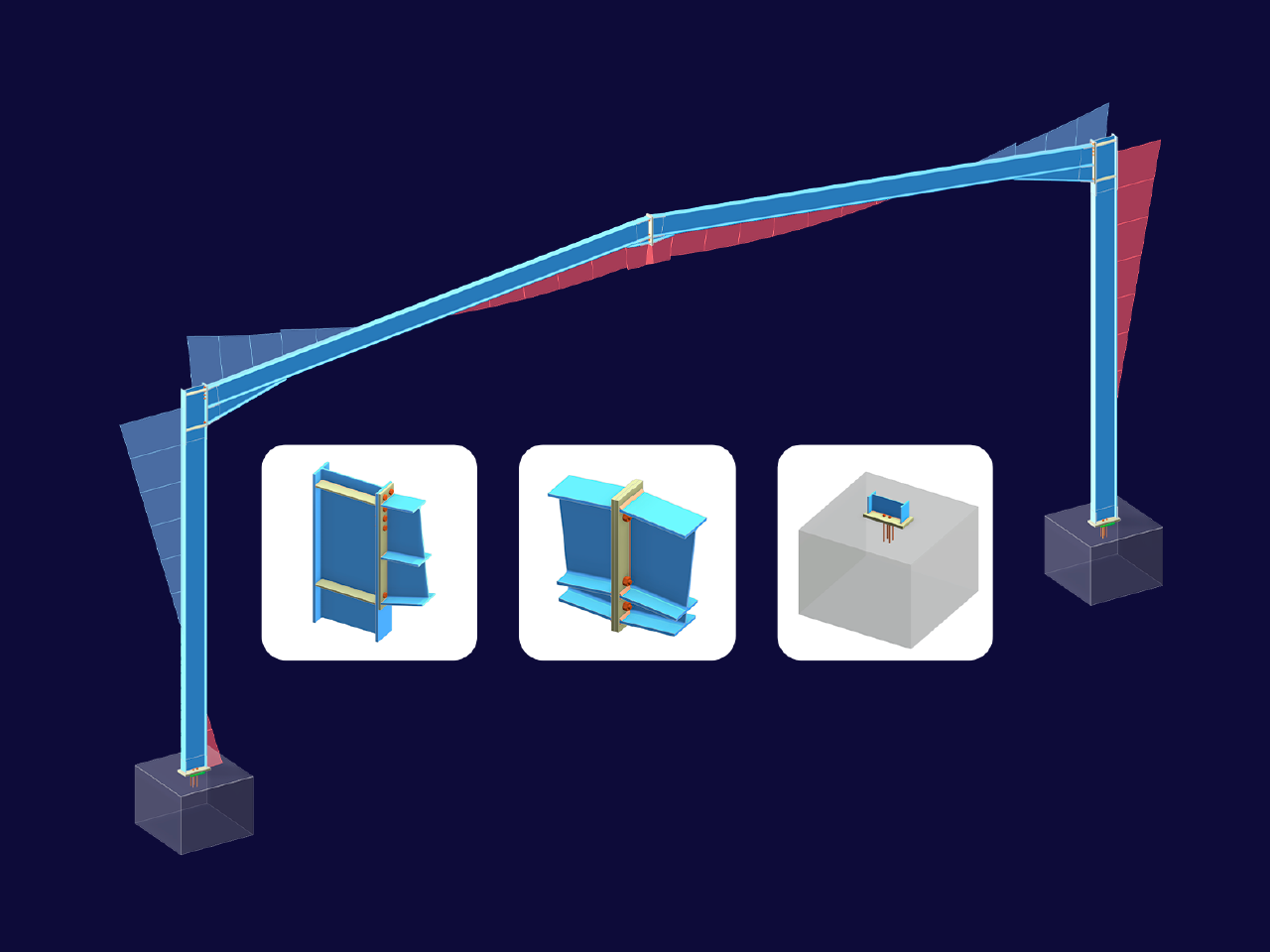
Di seguito, il significato di MRF è dimostrato utilizzando un semplice esempio. Un telaio a due cerniere con una singola colonna con estremità a perno (colonna destra) è considerato nel piano come mostrato nell'immagine 1. Viene eseguita un'analisi di stabilità lineare per la tensione mostrata, applicando le impostazioni predefinite.
Valutazione delle forme modali da parte degli ingegneri
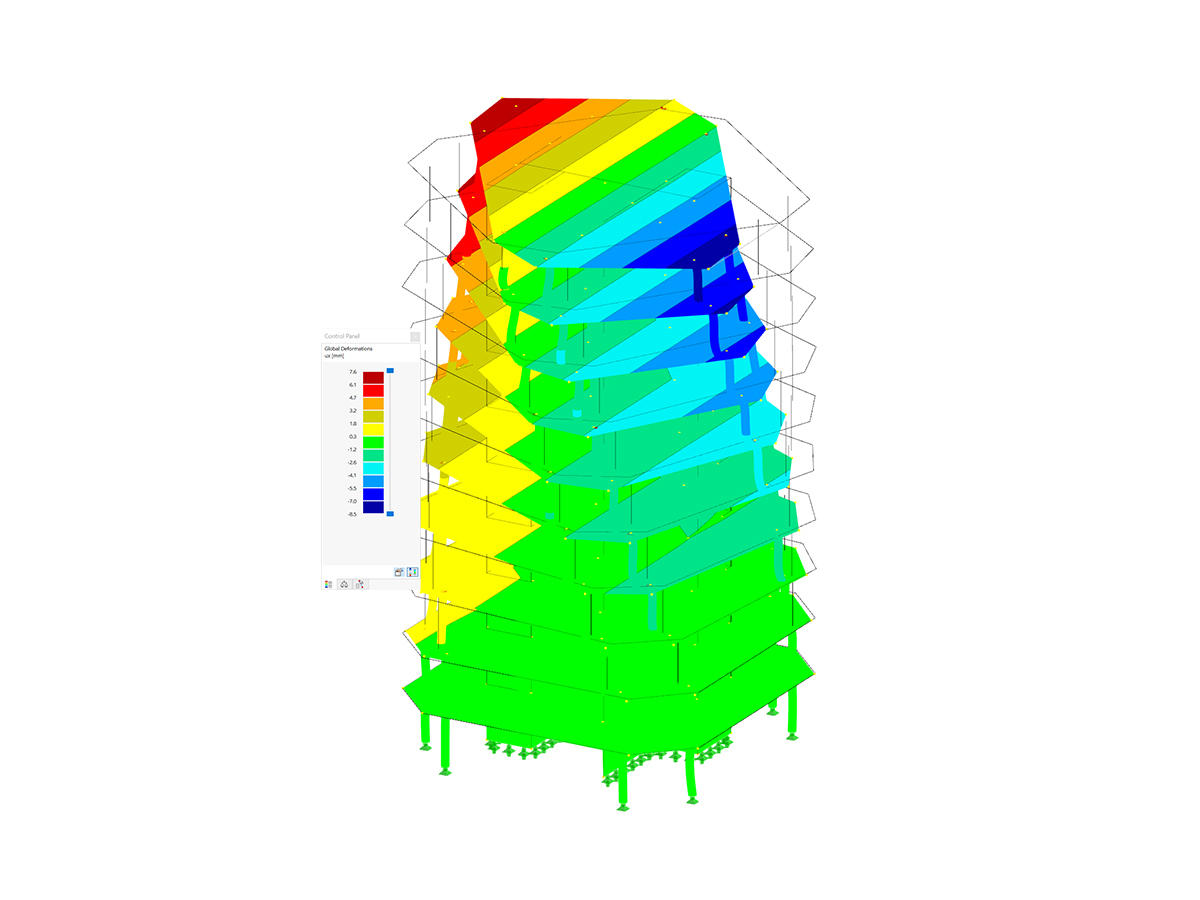
Le prime quattro forme modali della struttura sono mostrate nell'immagine 2; possono essere caratterizzati come segue:
- La prima forma modale è caratterizzata dall'instabilità laterale del telaio. Le aste con estremità a perno 4 e 5 mostrano grandi spostamenti, ma seguono solo il movimento laterale del telaio, in modo che non si verifichi alcuna energia di deformazione significativa in queste aste.
- Le forme modali 2 e 3, tuttavia, possono essere identificate come modi di instabilità isolati della colonna con estremità a perno (asta 5). Il telaio assicura un vincolo laterale della testa della colonna, in modo che la stabilità della colonna può essere idealizzata anche come modo di instabilità di Eulero II (forme del primo e del secondo modo intorno all'asse maggiore).
- Nella quarta forma modale, si può osservare l'instabilità delle colonne più corte, appartenenti al telaio a due cerniere. Tuttavia, come nella prima forma modale, la trave orizzontale collegata rigidamente contribuisce ad un aumento del carico critico.
Analisi obiettivo utilizzando MRF
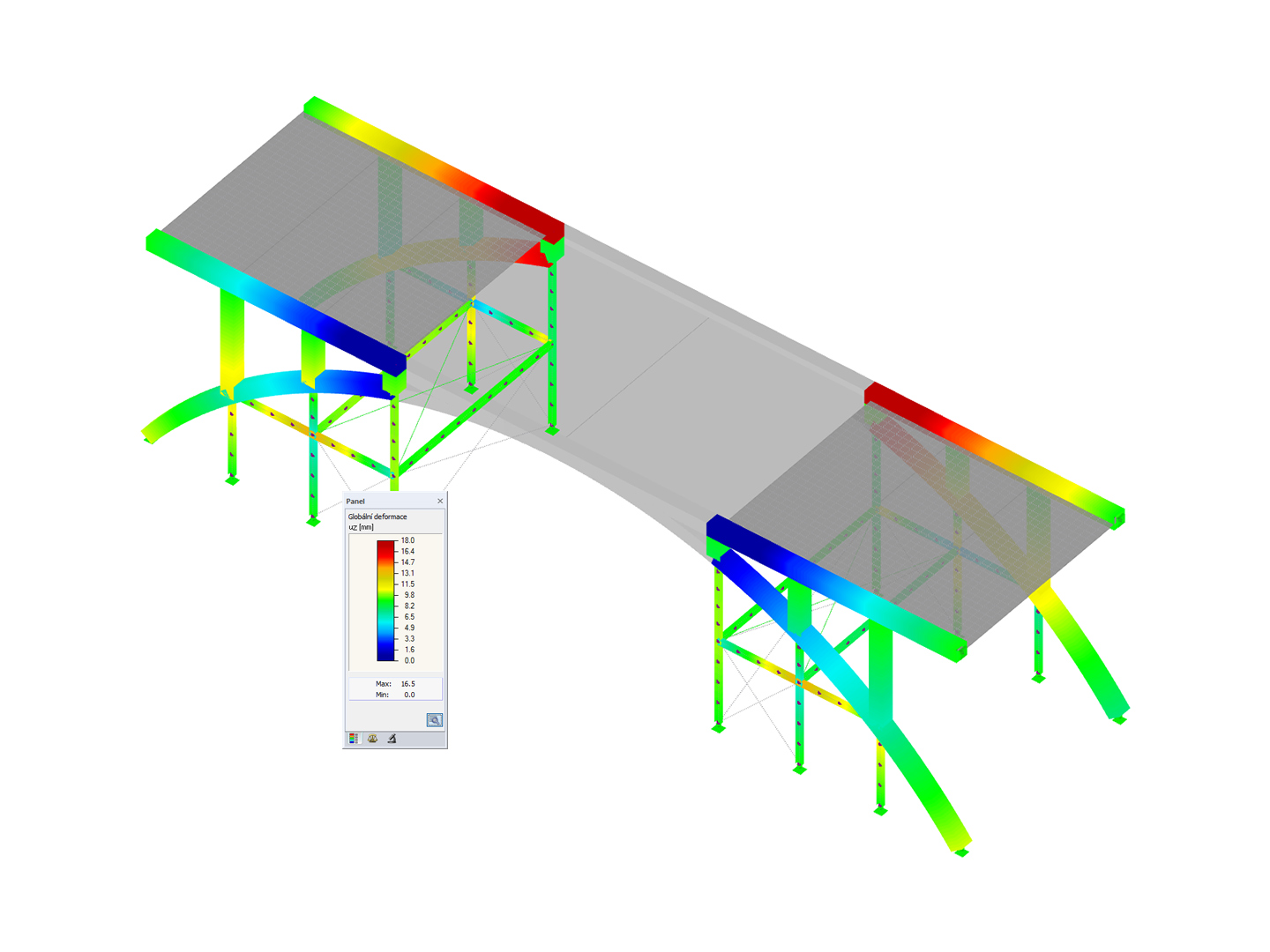
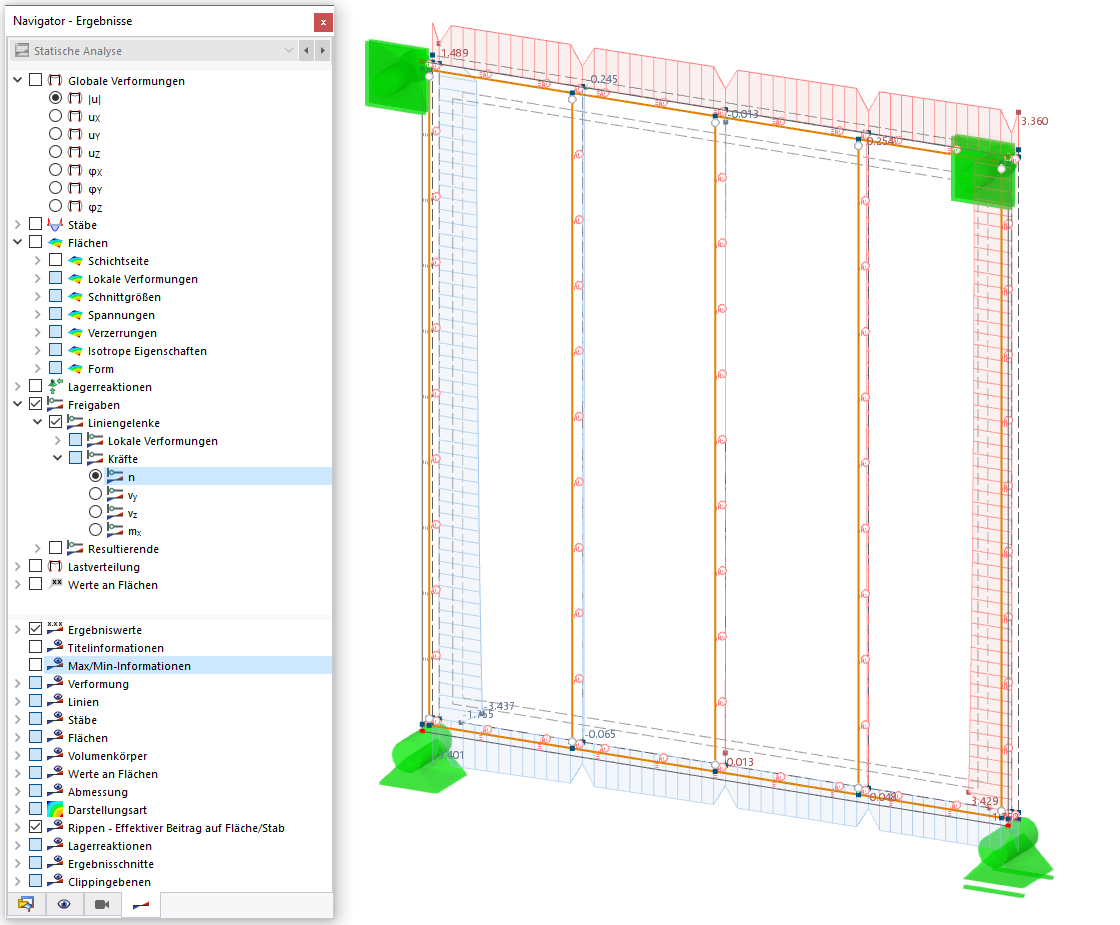
Oltre all'analisi "manuale" e alla valutazione delle forme modali, l'utente ha ora a sua disposizione un fattore ausiliario oggettivo. L'immagine 3 mostra la tabella dei risultati "Lunghezze efficaci e carichi critici per forma modale" per il sistema di esempio. I coefficienti di rilevanza modale calcolati per asta confermano che le forme modali 1 e 4 sono dominate dal telaio rigido (aste 1-3), mentre le aste con estremità a spillo 4 e 5 non hanno rilevanza (MRF = 0%). Al contrario, solo l'asta 5 (MRF = 100 %) partecipa alle forme modali 2 e 3 - una rapida occhiata alla tabella dei risultati rivela che queste forme modali devono essere un cedimento per stabilità locale.
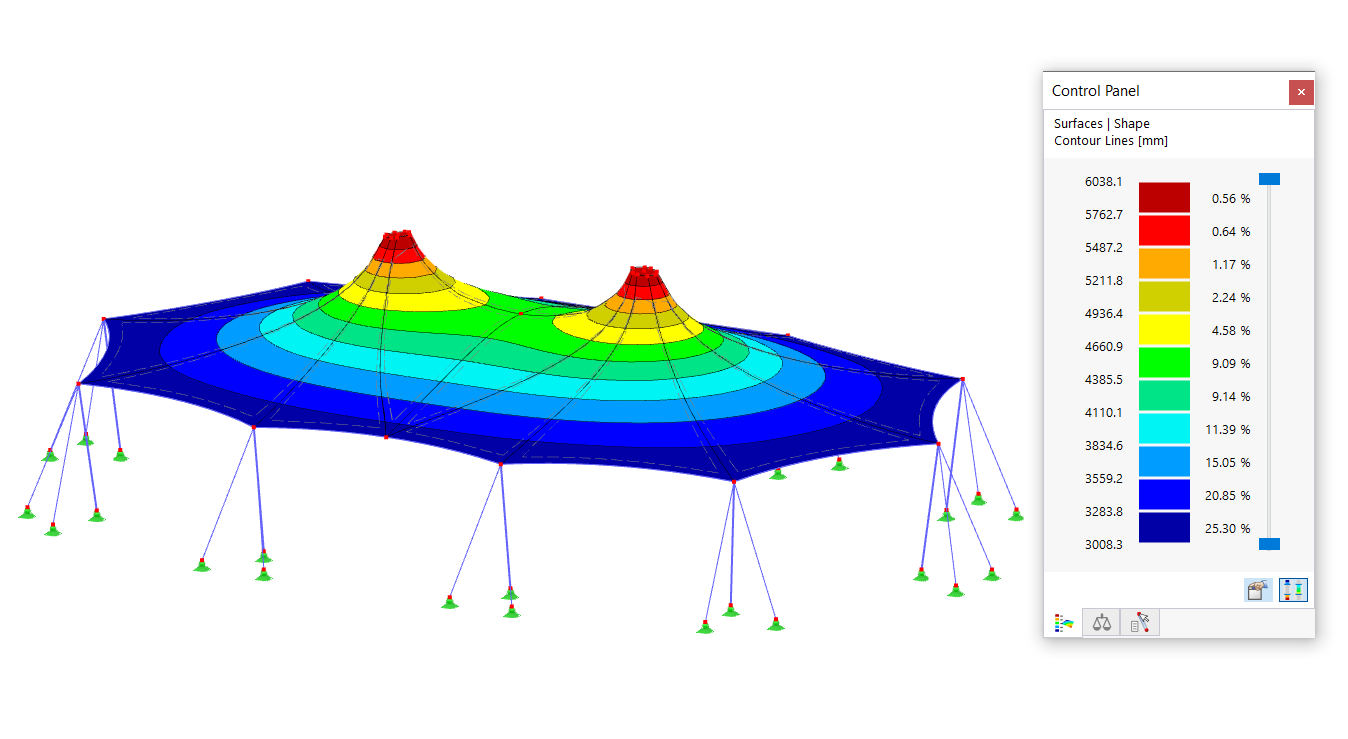
La rappresentazione asta per asta dei fattori di rilevanza modale (vedere la Figura 4) è adatta per determinare le lunghezze libere di inflessione e i carichi critici delle singole aste. L'esempio selezionato rappresenta un sistema strutturale planare; una deviazione dal piano del telaio (intorno all'asse dell'asta minore) non è possibile a causa delle impostazioni di base selezionate. Pertanto, solo l'asse forte (y-) è importante qui per l'analisi delle lunghezze efficaci determinanti e dei carichi critici.
I risultati mostrati nell'immagine 4 implicano che la prima forma modale dovrebbe essere applicata in un'analisi di stabilità dei montanti del telaio (aste 1 e 3). Qui, il carico critico è minimo per le forme modali in cui partecipano i montanti del telaio (1 e 4). Per l'analisi di instabilità intorno all'asse maggiore utilizzando il metodo dell'asta equivalente, dovrebbe essere selezionato un coefficiente di lunghezza di instabilità di 2,827. Per la colonna con estremità a perno (asta 5), tuttavia, la forma modale 2 con un coefficiente di lunghezza efficace di 1.016 sarebbe determinante. Qui viene calcolato anche il carico critico più basso per la forma modale 1, ma la colonna con estremità a spillo non partecipa a questa forma modale (MRF = 0 %).
Per rendere più chiara l'analisi MRF tabellare, è consigliabile filtrare tutti i MRF fino a un certo valore limite (ad esempio inferiore al 20%) utilizzando il "Gestore delle tabelle dei risultati".
