Dans le cadre du calcul des valeurs propres linéaires à l'aide du module complémentaire Stabilité de la structure, les « facteurs de pertinence modale » (MRF) sont désormais également affichés pour toutes les modes propres et les barres individuelles en plus des charges critiques et des longueurs efficaces équivalentes déterminées à partir de ces charges. La MRF décrit qualitativement la pertinence d'une barre pour un mode propre calculé. Le calcul est basé sur l'énergie de déformation élastique, qui résulte pour chaque barre individuelle (« k ») dans le mode propre (« i »). Étant donné que les modes propres peuvent être mis à l'échelle selon les besoins, aucune énergie de déformation absolue n'est considérée. Au lieu de cela, les énergies de toutes les barres individuelles sont mises en relation :
où
- « ui » - mode propre pour la valeur propre « i »
- « Kek » - matrice de rigidité des éléments pour la barre « k »
Un MRF de 100 % signifie qu'une seule barre a une pertinence maximale pour le mode propre considéré. Les barres qui n'ont pas d'énergie de déformation significative en comparaison n'ont cependant aucun intérêt pour le mode propre considéré.
Dans le cadre de l'évaluation de l'analyse de stabilité par mode propre, le MRF permet de différencier rapidement et systématiquement les modes propres locaux et globaux. Si plusieurs barres individuelles ont un MRF significatif pour un mode propre (par exemple supérieur à 20 %), cela indique une instabilité de la structure entière ou d'une structure partielle. D'un autre côté, si la somme de toutes les MRF pour un mode propre est d'environ 100 %, un phénomène de stabilité local (par exemple le flambement d'une barre unique) est à prévoir.
De plus, le MRF peut être utilisé pour déterminer les charges critiques déterminantes et les longueurs efficaces équivalentes de certaines barres (par exemple pour la vérification de la stabilité). Il est recommandé ici d'évaluer les résultats de l'analyse barre par barre. Les modes propres pour lesquels la barre a des valeurs MRF faibles (par exemple moins de 20 %) peuvent facilement être négligés dans la recherche de la longueur efficace critique de la barre.
Exemple
Dans ce qui suit, l'importance de la MRF est démontrée à l'aide d'un exemple simple. Un portique à deux articulations avec un poteau pendulaire individuel (poteau de droite) est considéré dans le plan comme le montre la Figure 1. Une analyse de stabilité linéaire est effectuée pour la contrainte affichée en appliquant les paramètres par défaut.
Évaluation des modes propres par l'expertise technique
Les quatre premiers modes propres de la structure sont illustrés dans la Figure 2, ils peuvent être caractérisés comme suit :
- Le premier mode propre est caractérisé par l'instabilité latérale du portique. Les barres pendulaires 4 et 5 présentent des déplacements importants, mais ne suivent que le mouvement latéral du portique, de sorte qu'aucune énergie de déformation significative n'apparaît dans ces barres.
- Les modes propres 2 et 3 peuvent cependant être identifiés comme des formes de flambement isolées du poteau pendulaire (barre 5). Le portique assure un appui latéral du poteau, de sorte que la stabilité du poteau peut également être idéalisée comme mode de flambement selon Euler II (premier et deuxième mode propre autour de l'axe principal).
- Dans le quatrième mode propre, le flambement des poteaux les plus courts, appartenant au portique à deux articulations, peut être observé. Cependant, comme dans le premier mode propre, la poutre rigidement connectée contribue à une augmentation de la charge critique.
Analyse objective à l'aide du MRF
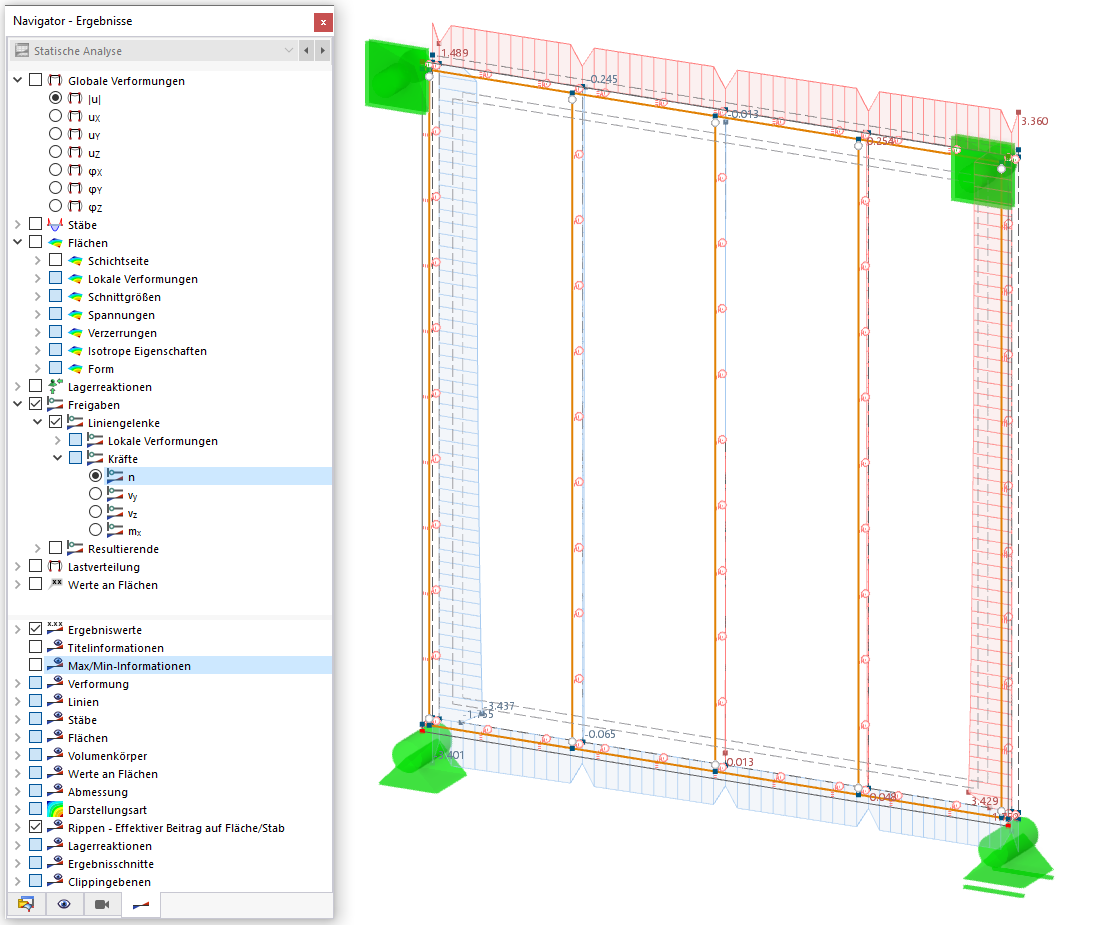
Outre l'analyse et l'évaluation « manuelles » des modes propres, l'utilisateur dispose désormais avec le MRF d'un facteur auxiliaire objectif. La Figure 3 montre le tableau de résultats « Longueurs efficaces et charges critiques par mode propre » pour l'exemple de système. Les facteurs de pertinence modale calculés par barre confirment que les modes propres 1 et 4 sont dominés par le portique rigide (barres 1-3), tandis que les barres pendulaires 4 et 5 n'ont aucune pertinence (MRF = 0 %). En revanche, seule la barre 5 (MRF = 100 %) participe aux modes 2 et 3, un rapide coup d'œil au tableau de résultats révèle que ces modes doivent être une rupture de stabilité locale.
La représentation par barre des facteurs de pertinence modale (voir la Figure 4) permet de déterminer les longueurs efficaces et les charges critiques déterminantes des barres individuelles. L'exemple sélectionné représente un système structurel plan, un écart par rapport au plan du cadre (autour de l'axe de barre secondaire) n'est pas possible en raison des paramètres de base sélectionnés. Ainsi, seul l'axe (y-) fort est important ici pour l'analyse des longueurs efficaces déterminantes et des charges critiques.
Les résultats présentés dans la Figure 4 impliquent que la première forme de mode doit être appliquée dans une analyse de stabilité des poteaux de portique (barres 1 et 3). Parmi les modes propres auxquels participent les poteaux de charpente (1 et 4), la charge critique est ici minimale. Pour l'analyse de flambement autour de l'axe principal à l'aide de la méthode de barre équivalente, un coefficient de longueur de flambement de 2,827 doit être sélectionné. Cependant, pour le poteau articulé (barre 5), le mode propre 2 avec un coefficient de longueur efficace de 1,016 serait déterminant. La charge critique la plus faible est également calculée ici pour le mode propre 1, mais le poteau pendulaire ne participe pas à cette modalité (MRF = 0 %).
Afin de rendre l'analyse tabulaire du MRF plus claire, il est recommandé de filtrer tous les MRF jusqu'à une certaine valeur limite (par exemple moins de 20 %) à l'aide du « Gestionnaire du tableau de résultats ».
.png?mw=600&hash=49b6a289915d28aa461360f7308b092631b1446e)
