W ramach obliczania liniowej wartości własnej przy użyciu rozszerzenia Stateczność konstrukcji, oprócz obciążeń krytycznych i równoważnych długości efektywnych określonych na podstawie tych obciążeń, wyświetlane są teraz również "Modalne współczynniki istotności" (ang. MRF - Modal Relevance Factors) dla wszystkich kształtów drgań i dla poszczególnych prętów. MRF opisuje jakościowo istotność pręta dla obliczonego kształtu drgań. Obliczenia opierają się na energii odkształcenia sprężystego dla każdego pręta (k) w kształcie drgań (i). Ponieważ kształty drgań mogą być skalowane zgodnie z wymaganiami, nie są uwzględniane bezwzględne energie odkształcenia. Zamiast tego, energie wszystkich pojedynczych prętów są odnoszone do siebie:
gdzie
- ui - kształt drgań dla wartości własnej i
- Kek - macierz sztywności elementu dla pręta k
MRF równy 100% oznacza, że pojedynczy pręt ma maksymalne znaczenie dla rozpatrywanego kształtu drgań. Pręty, które w porównaniu z tym nie mają znaczącej energii odkształcenia, nie są jednak istotne dla rozpatrywanego kształtu drgań.
W ramach analizy stateczności według kształtu drgań, model MRF może być wykorzystany do szybkiego i systematycznego rozróżniania między lokalnymi i globalnymi kształtami drgań. Jeżeli kilka pojedynczych prętów ma znaczący MRF dla kształtu drgań (np. większy niż 20%), wskazuje to na niestateczność całej konstrukcji lub jej części. Z drugiej strony, jeżeli suma wszystkich MRF dla kształtu drgań wynosi około 100%, należy spodziewać się lokalnego zjawiska stateczności (np. wyboczenia pojedynczego pręta).
Ponadto MRF można wykorzystać do określenia decydujących obciążeń krytycznych i równoważnych długości efektywnych niektórych prętów (np. do obliczeń stateczności). W tym przypadku zalecana jest ocena wyników analizy dla prętów. Kształty drgań, dla których pręt ma małe wartości MRF (np. mniejsze niż 20%), można łatwo pominąć podczas wyszukiwania efektywnej długości krytycznej pręta.
Przykład
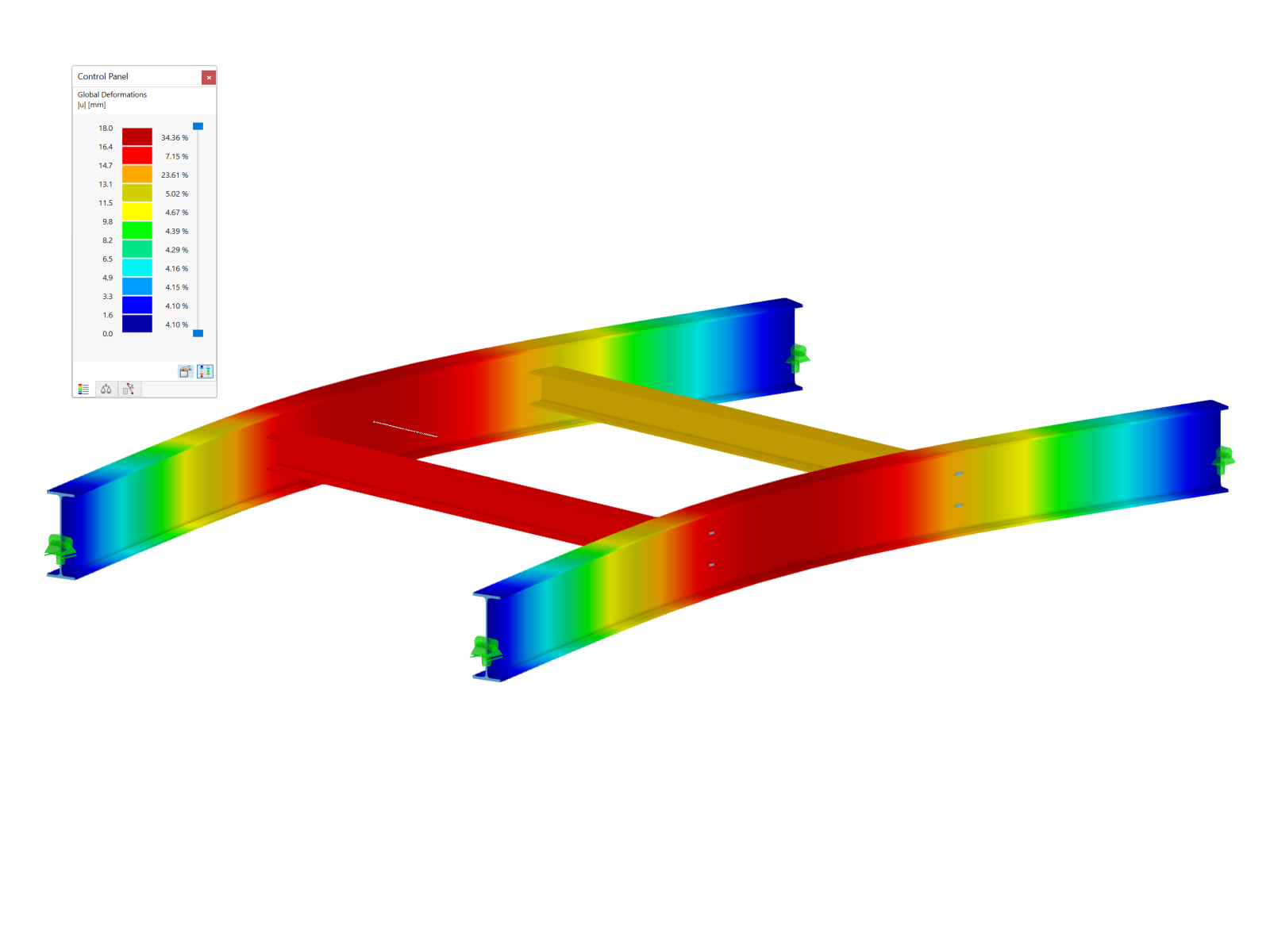
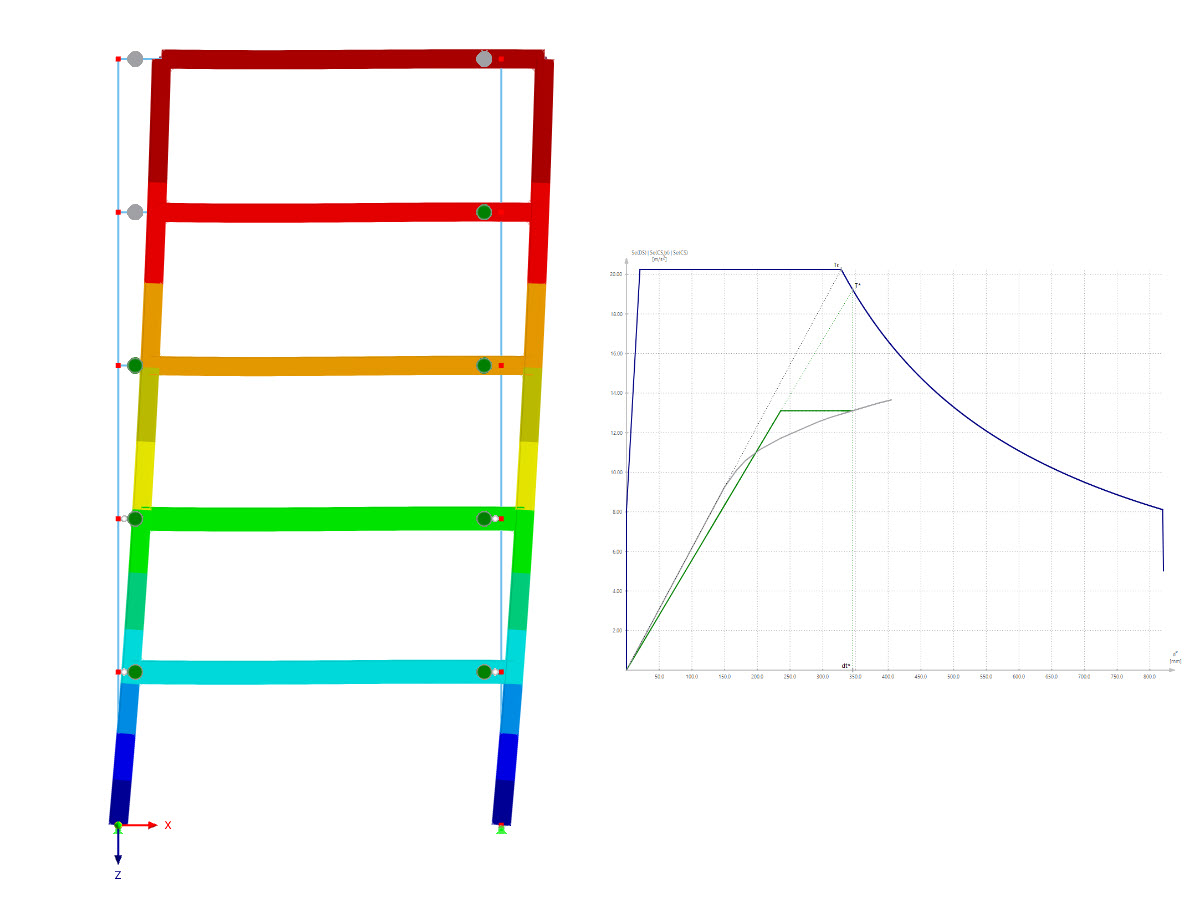
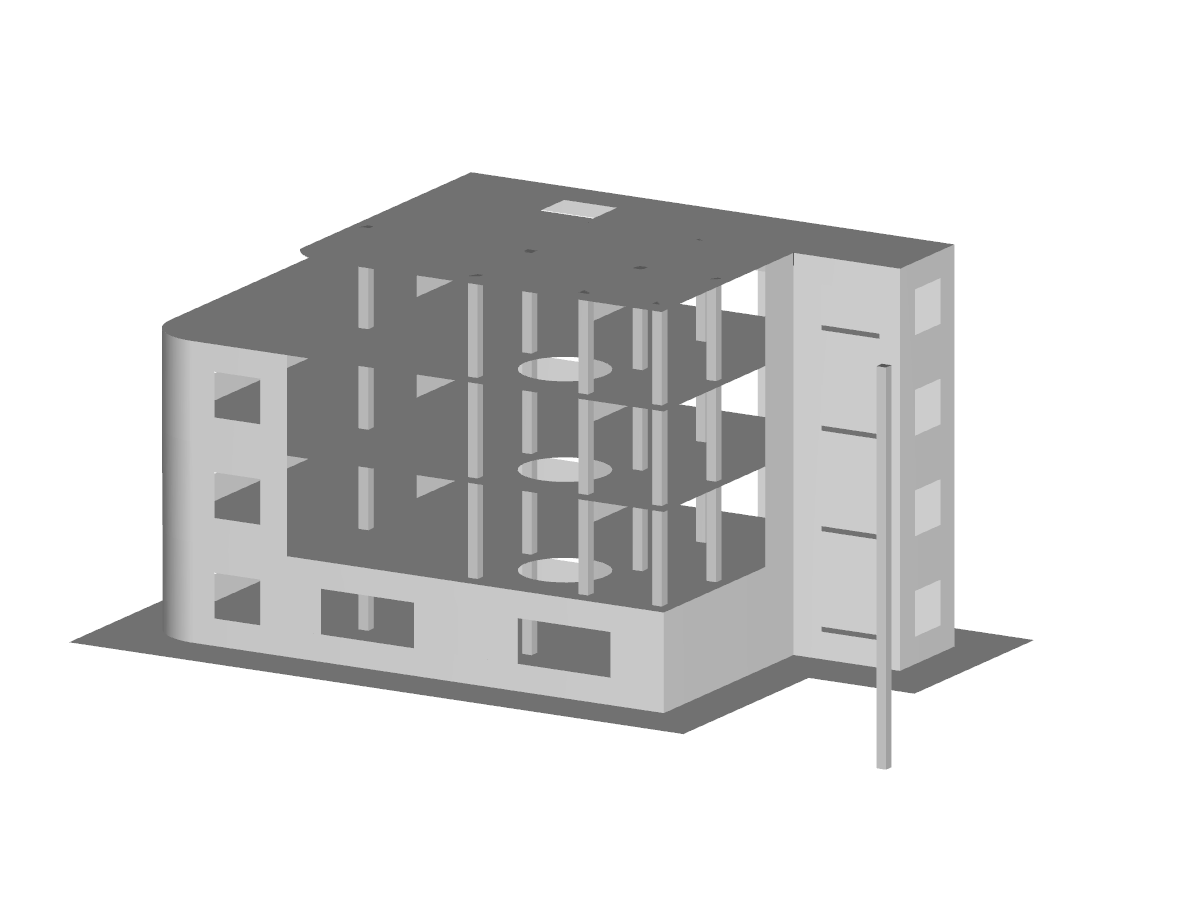
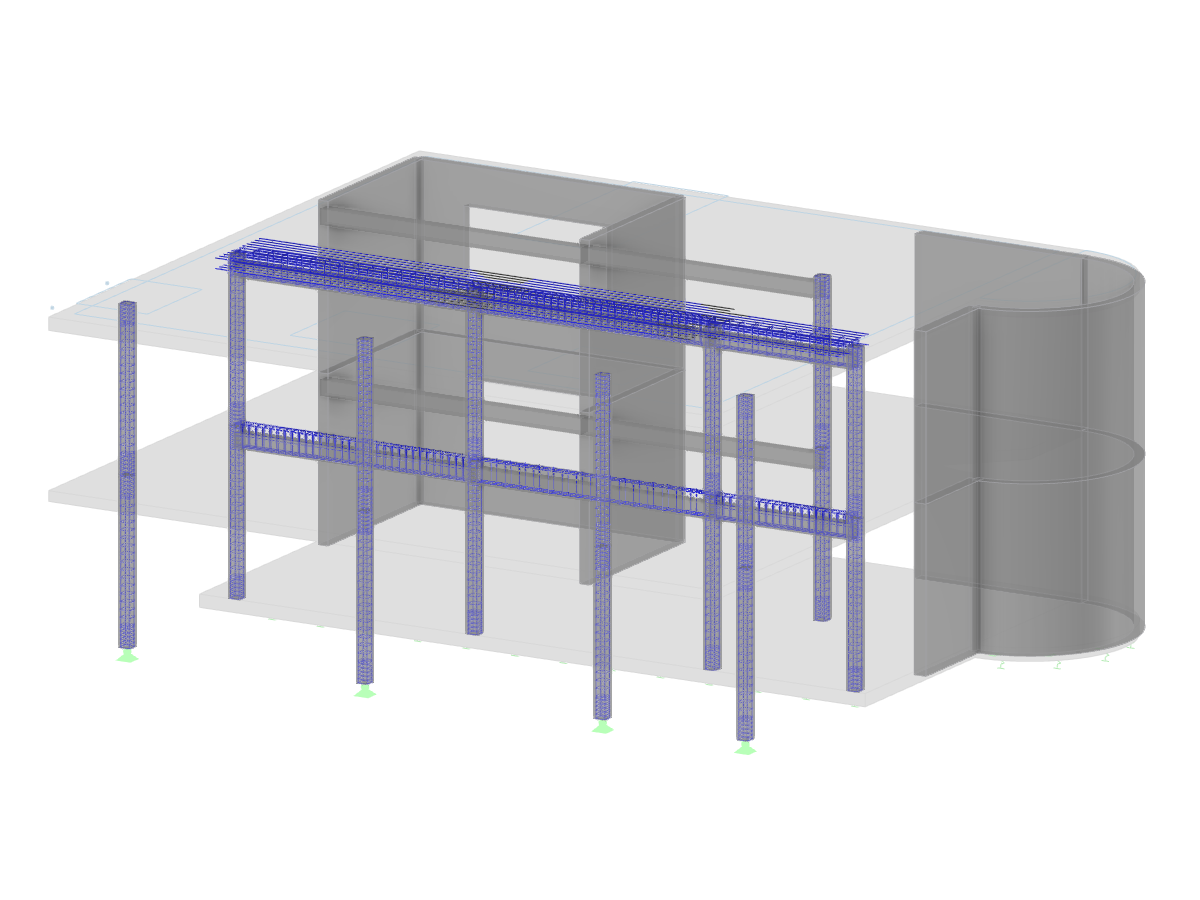
Poniżej, na prostym przykładzie, zademonstrowano znaczenie MRF. Rama dwuprzegubowa z pojedynczym słupem zakończonym sworzniem (prawy słup) jest rozpatrywana w płaszczyźnie, jak pokazano na rysunku 1. Dla pokazanego naprężenia przeprowadzana jest liniowa analiza stateczności z zastosowaniem ustawień domyślnych.
Ocena kształtu drgań na podstawie wiedzy inżynierskiej
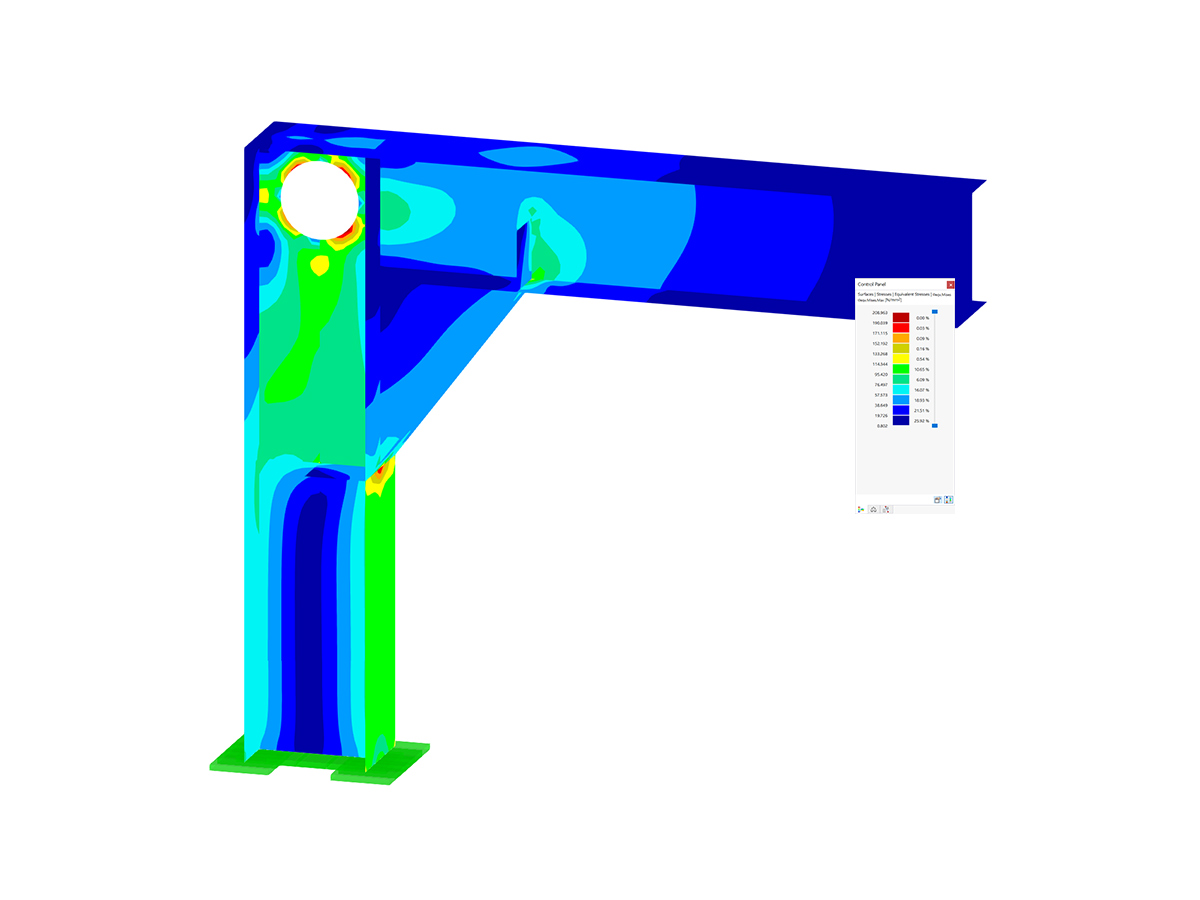
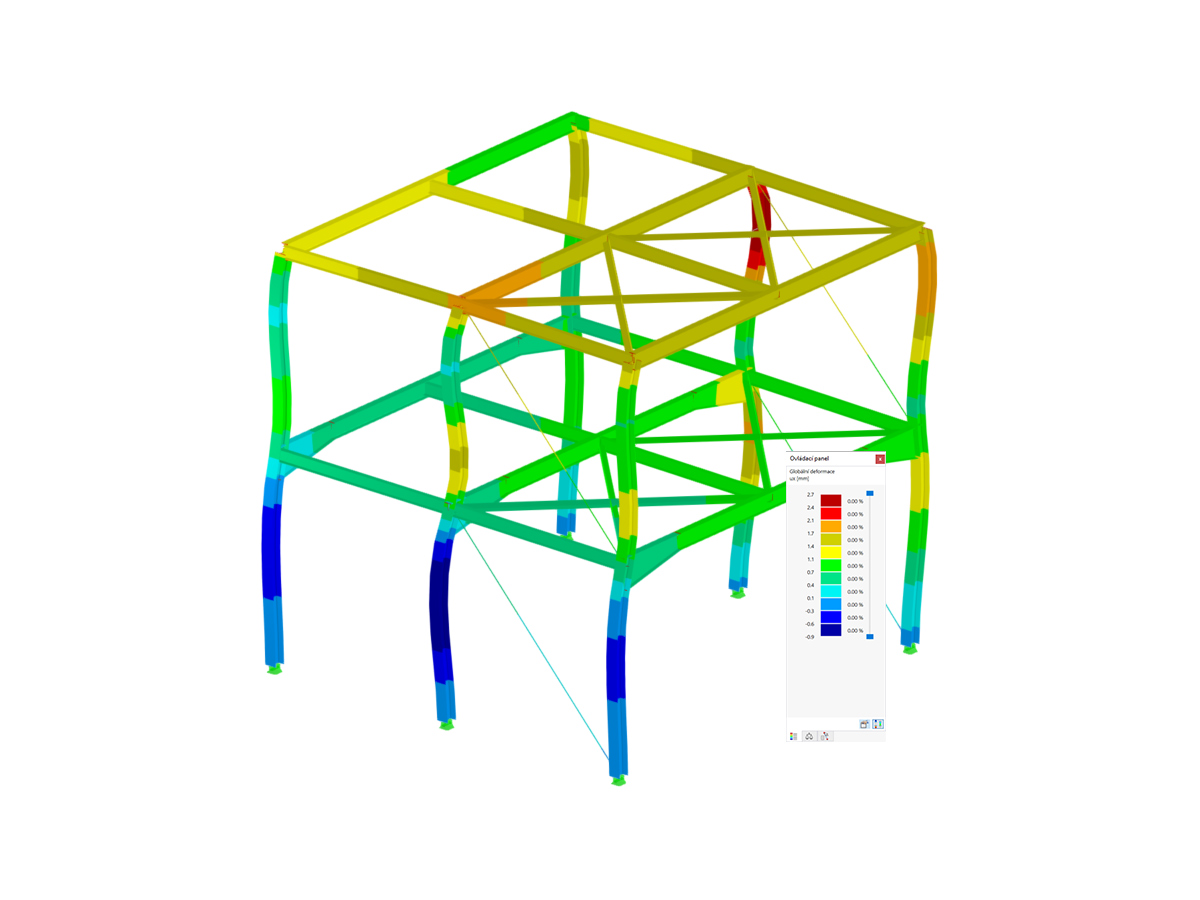
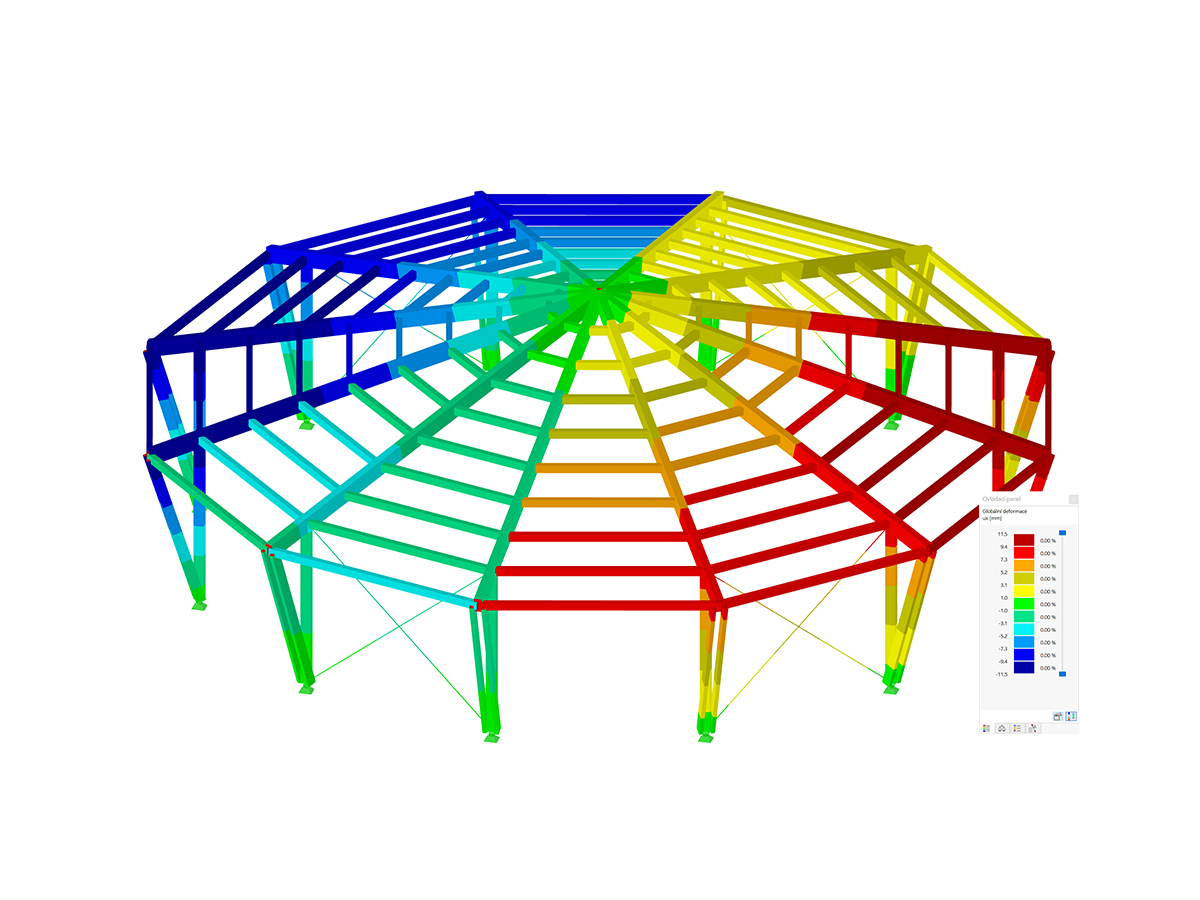
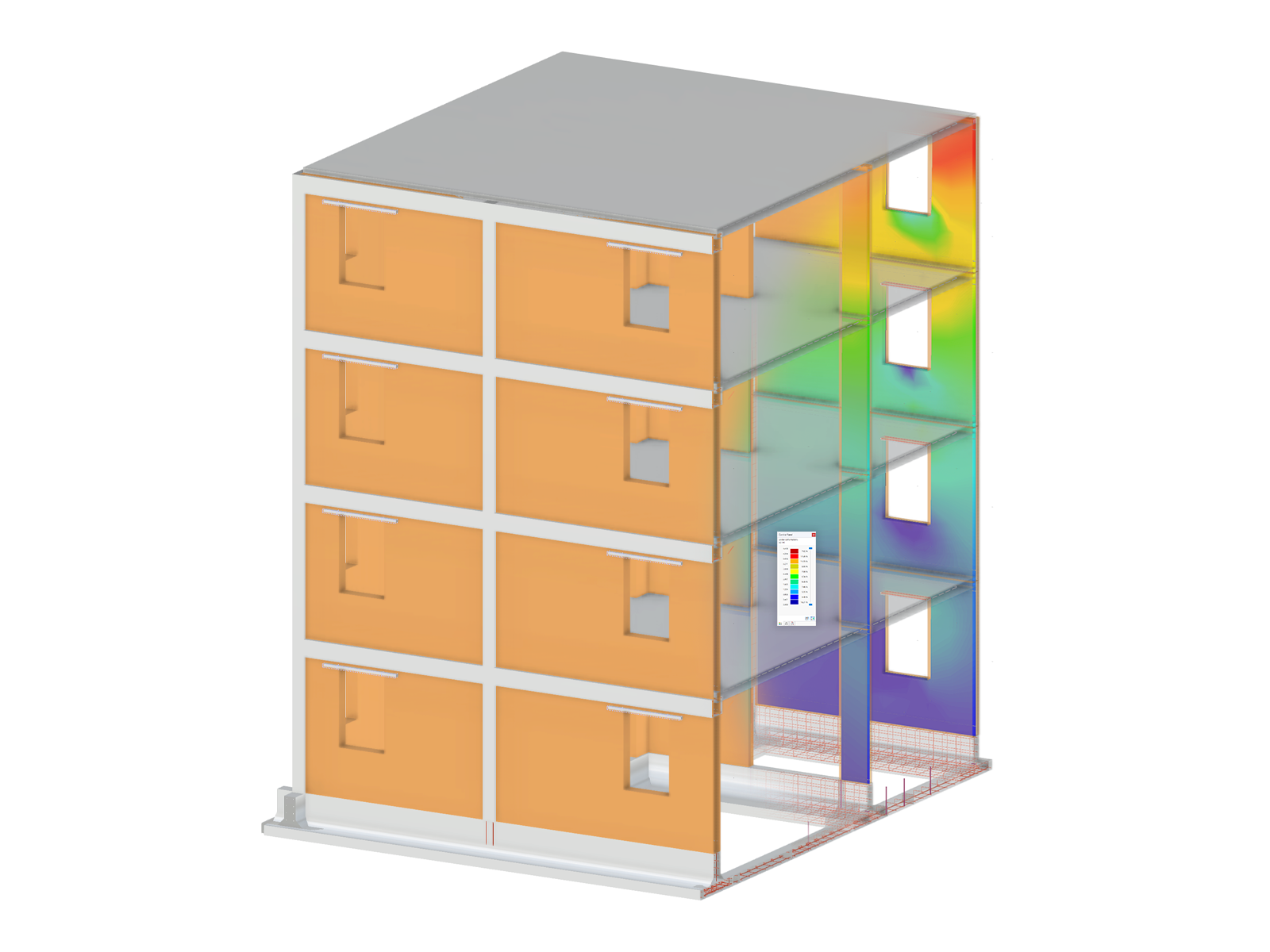
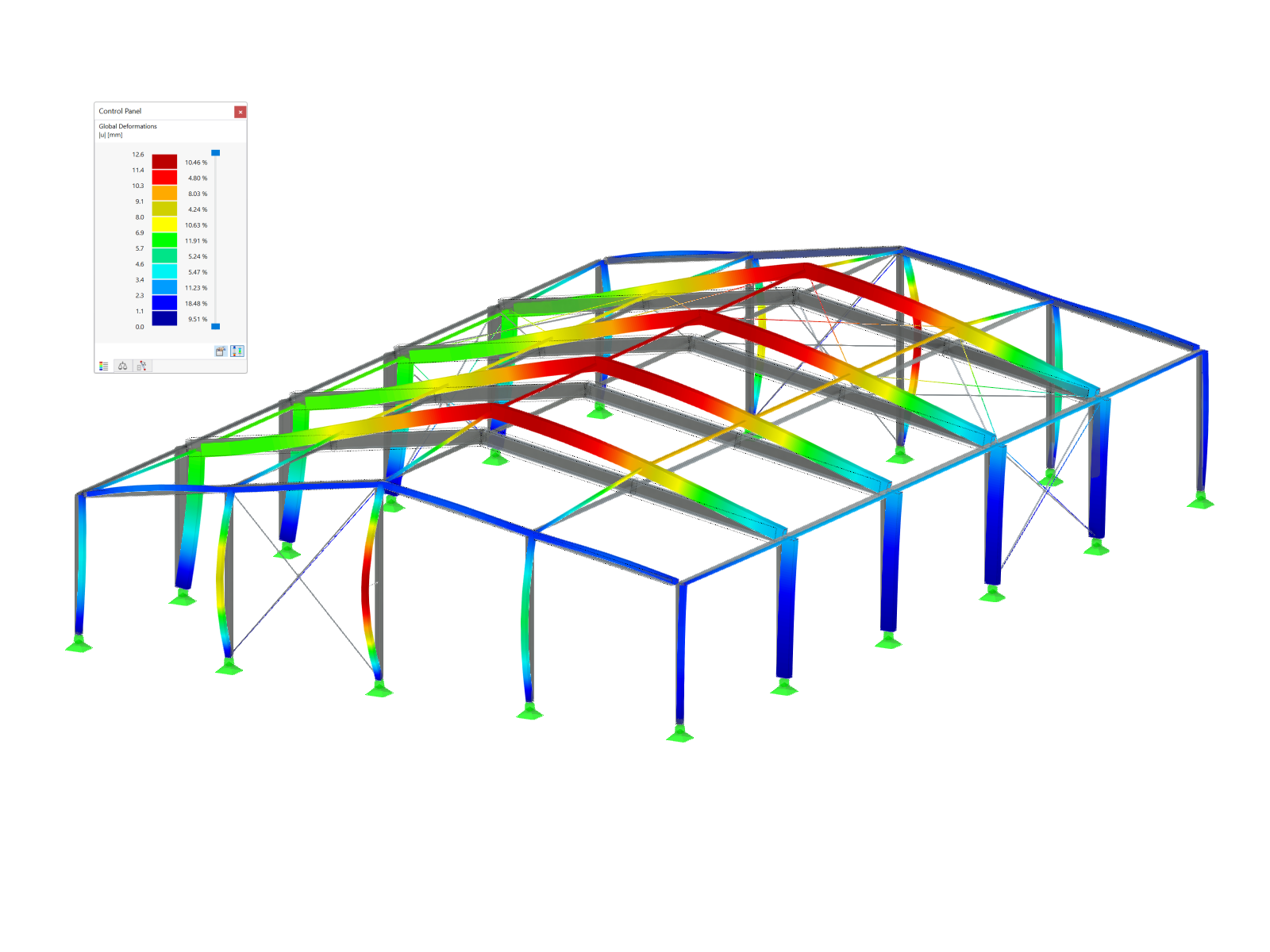
Pierwsze cztery kształty drgań konstrukcji pokazano na rys. 2; można je scharakteryzować następująco:
- Pierwszy kształt drgań jest scharakteryzowany przez boczną niestateczność ramy. Pręty przegubowe 4 i 5 wykazują duże przemieszczenia, ale podążają za ruchem bocznym ramy, tak że w tych elementach nie powstaje żadna znacząca energia odkształcenia.
- Kształty drgań 2 i 3 można natomiast zidentyfikować jako wyodrębnione wyboczenia słupa (pręt 5) zakończonego sworzniem. Rama zapewnia boczne podparcie głowicy słupa, dzięki czemu stateczność słupa można również wyidealizować jako postać II wyboczenia Eulera (pierwszy i drugi kształt względem osi głównej).
- W czwartym kształcie można zaobserwować wyboczenie krótszych słupów ramy dwuprzegubowej. Jednak, podobnie jak w pierwszym kształcie drgań, sztywno połączona belka pozioma przyczynia się do wzrostu obciążenia krytycznego.
Obiektywna analiza z wykorzystaniem MRF
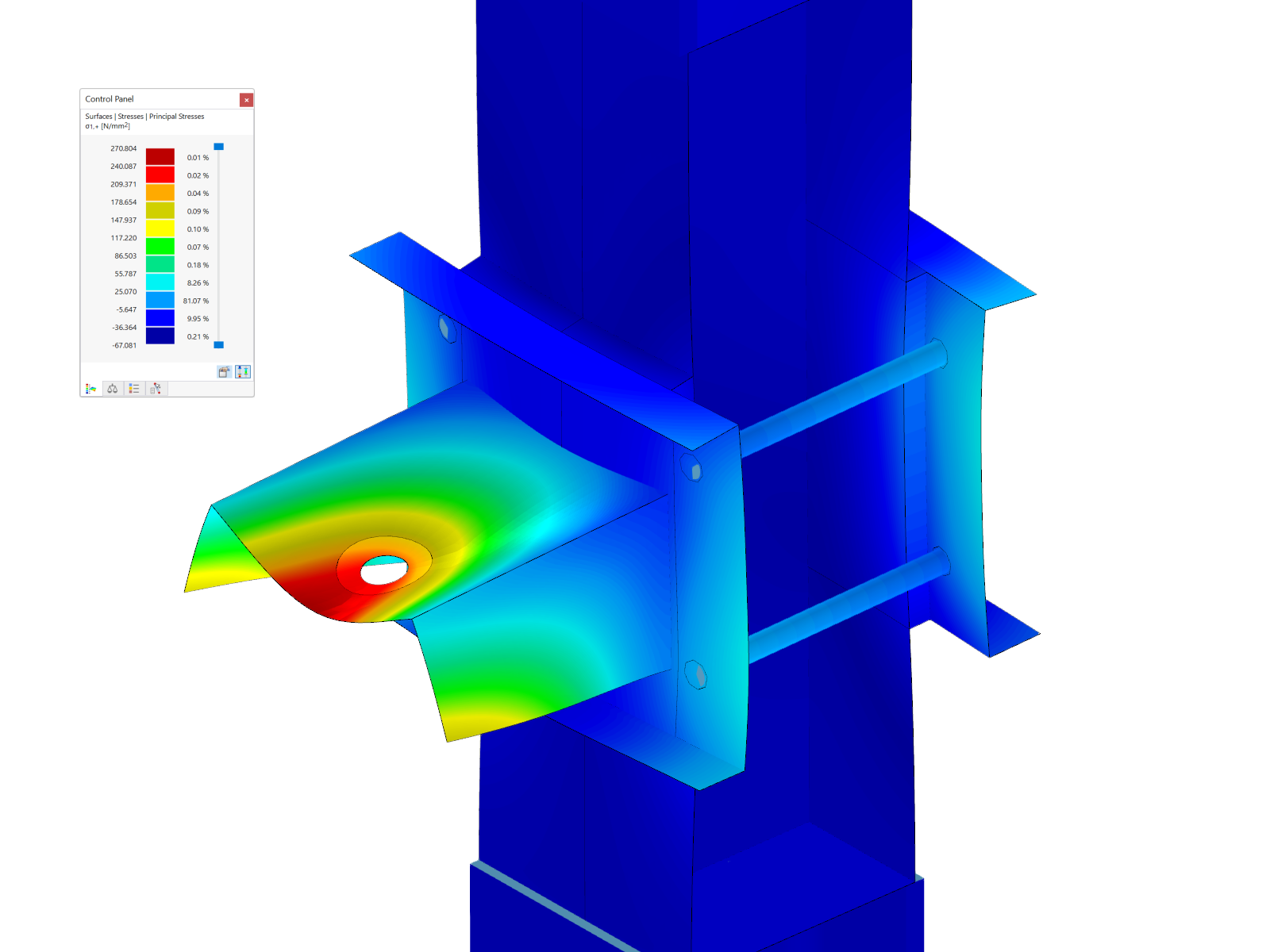
Oprócz „ręcznej” analizy i oceny kształtu drgań, użytkownik ma teraz do dyspozycji obiektywny czynnik pomocniczy. Rysunek 3 przedstawia tabelę wyników "Długości efektywne i obciążenia krytyczne według kształtu drgań" dla przykładowego układu. Modalne współczynniki istotności obliczone dla pręta potwierdzają, że kształty drgań 1 i 4 są zdominowane przez sztywną ramę (pręty 1-3), podczas gdy pręty podwieszone 4 i 5 nie mają znaczenia (MRF = 0%). W przeciwieństwie do tego, tylko pręt 5 (MRF = 100%) bierze udział w kształtach drgań 2 i 3 - szybkie spojrzenie na tabelę wyników pokazuje, że te kształty drgań muszą być lokalnym uszkodzeniem stateczności.
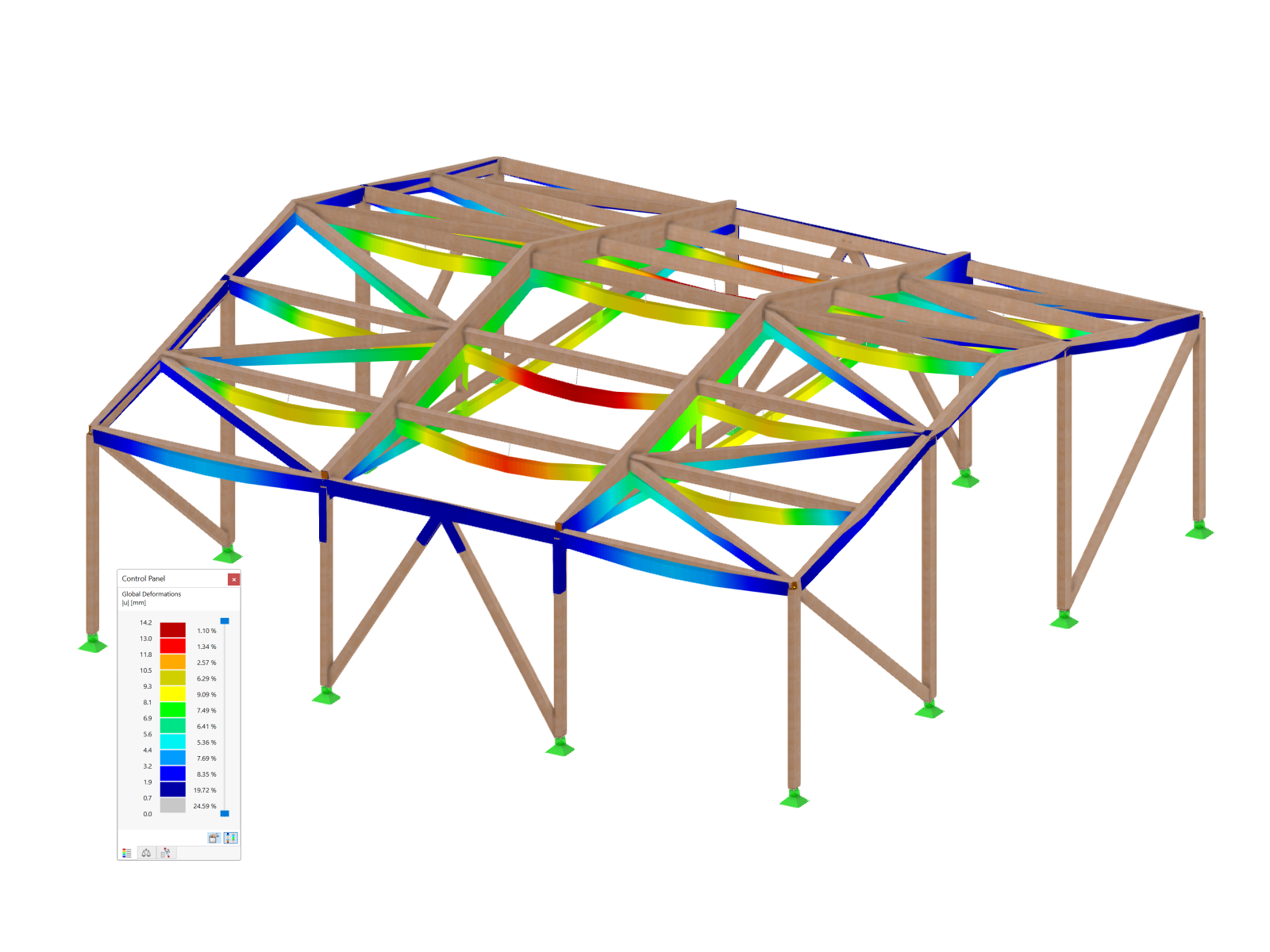
Reprezentacja modalnych współczynników istotności pręt po pręcie (patrz rysunek 4) jest odpowiednia do określania decydujących długości efektywnych i obciążeń krytycznych poszczególnych prętów. Wybrany przykład przedstawia płaski układ konstrukcyjny; ze względu na wybrane ustawienia podstawowe nie jest możliwe odchylenie od płaszczyzny ramy (względem osi pręta pomocniczego). Dlatego tylko oś główna (y) jest tutaj istotna dla analizy decydujących długości efektywnych i obciążeń krytycznych.
Wyniki pokazane na rys. 4 sugerują, że pierwszy kształt drgań powinien zostać zastosowany w analizie stateczności słupków ramy (prętów 1 i 3). Spośród kształtów drgań, w których uczestniczą słupki ramy (1 i 4), obciążenie krytyczne jest tutaj minimalne. W przypadku analizy wyboczeniowej względem osi głównej metodą pręta zastępczego należy wybrać współczynnik długości wyboczeniowej 2.827. Jednak w przypadku słupa przegubowego (pręt 5) decydująca byłaby postać drgań własnych 2 o współczynniku długości efektywnej równym 1.016. W tym miejscu obliczane jest również najniższe obciążenie krytyczne dla kształtu drgań 1, ale słup przegubowy nie bierze udziału w tym kształcie (MRF = 0%).
Aby analiza tabelaryczna MRF była bardziej przejrzysta, zaleca się odfiltrowanie wszystkich MRF do określonej wartości granicznej (np. poniżej 20%) za pomocą "Menedżera tabel wyników".
.png?mw=600&hash=49b6a289915d28aa461360f7308b092631b1446e)
