Stiffening of Structures

Finite element analysis software such as RFEM allow you to determine internal forces and design stiffening structural elements. In this program, you can model a building including all structural components, openings, and other elements, and perform a calculation of the entire model.

Pre-dimensioning of the stiffening system can be performed using manual calculation according to the calculation method described in [1], or by using a program such as SHAPE‑THIN. This software provides engineers with a better understanding of the load transfer in a structure as well as the resistance contribution of the individual structural components.

Distribution of Horizontal Forces

The horizontal load distribution for bending or torsional loading on the stiffening components can be calculated according to the following formulas.

Forces due to Bending

where
V_y,i, V_{z,i is the} shear force in the y- or z‑direction, which affects the partial cross‑section i,
V_y, V_z is the shear force in the y- or z‑direction, which affects the gross cross‑section,
I_y,i, I_z,i, I_yz,i are the moments of inertia of the partial cross‑section i relating to the parallel axes Y and Z by the partial cross‑section centroid S_i,
I_y, I_z are the total second moments of area relating to the overall centroid S.

Forces due to Torsion

where
V_y,i, V_{z,i is the} shear force in the y- or z‑direction, which affects the partial cross‑section i,
M_xs is the secondary torsional moment, which affects the gross cross‑section,
I_y,i, I_z,i, I_yz,i are the moments of inertia of the partial cross‑section i relating to the parallel axes Y and Z by the partial cross‑section centroid S_i,
I_ω,i is the warping constant related to the shear center M_i of the partial cross-section,
y_M,i, z_M,i is the coordinate of the shear center of the partial cross‑section M_i,
y_M, z_M is the coordinate of the overall shear center M.

Example

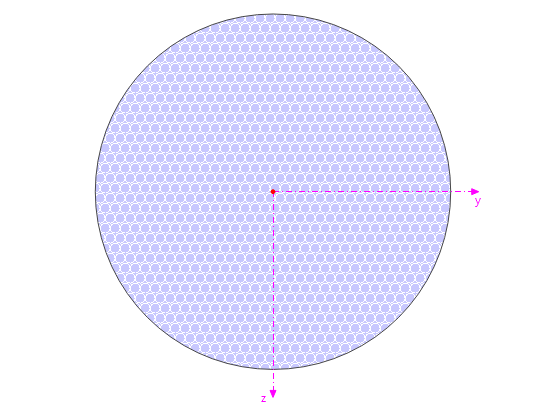
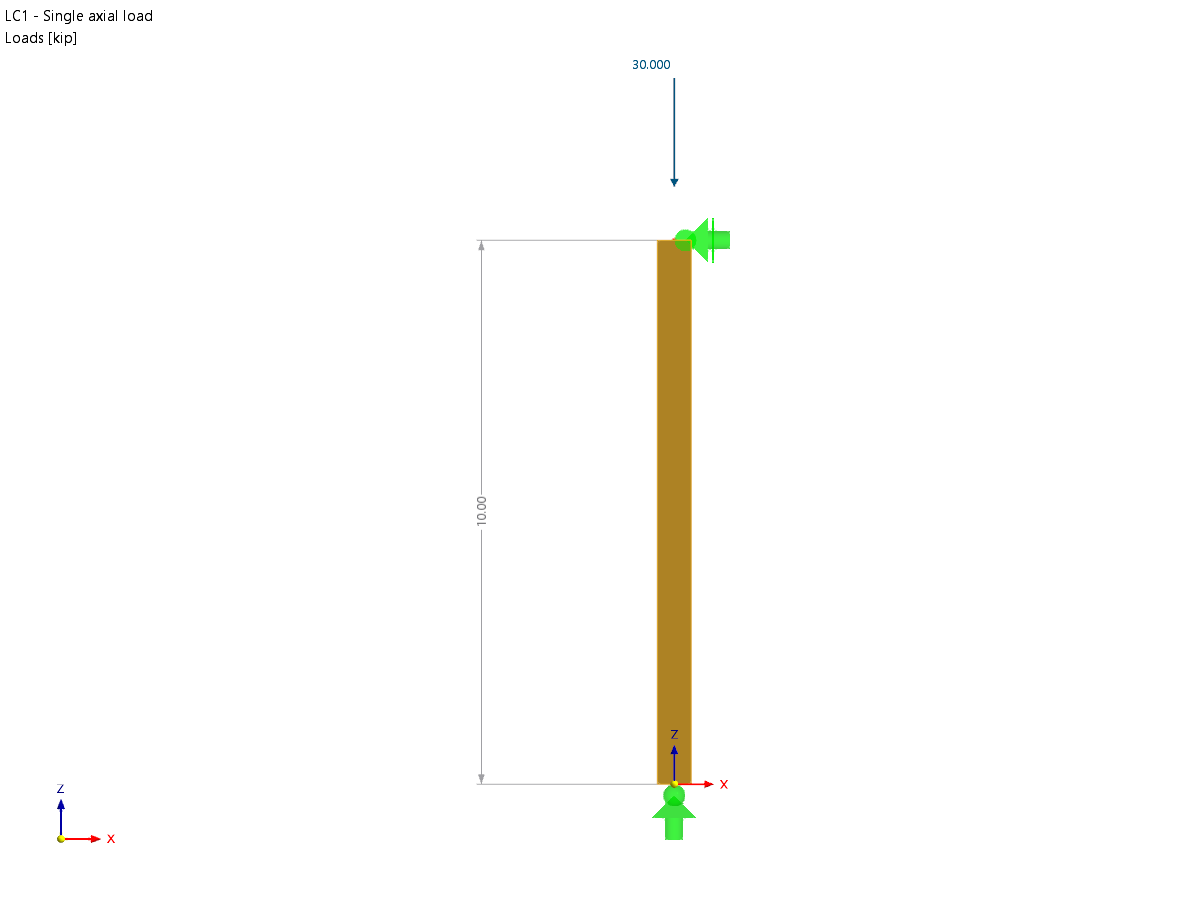
The distribution of horizontal loads in the stiffening elements is explained on the system displayed in Image 01.

Wall thickness t = 30 cm

Section Properties

Partial Cross-Section 1

Partial Cross-Section 2

Gross Cross-Section
I_y = 10.668 + 1.600 = 12.268 m⁴
I_z = 1.084 + 0.009 = 1.093 m⁴

The cross-section properties ​​determined in SHAPE-THIN 8 are displayed in Image 02.

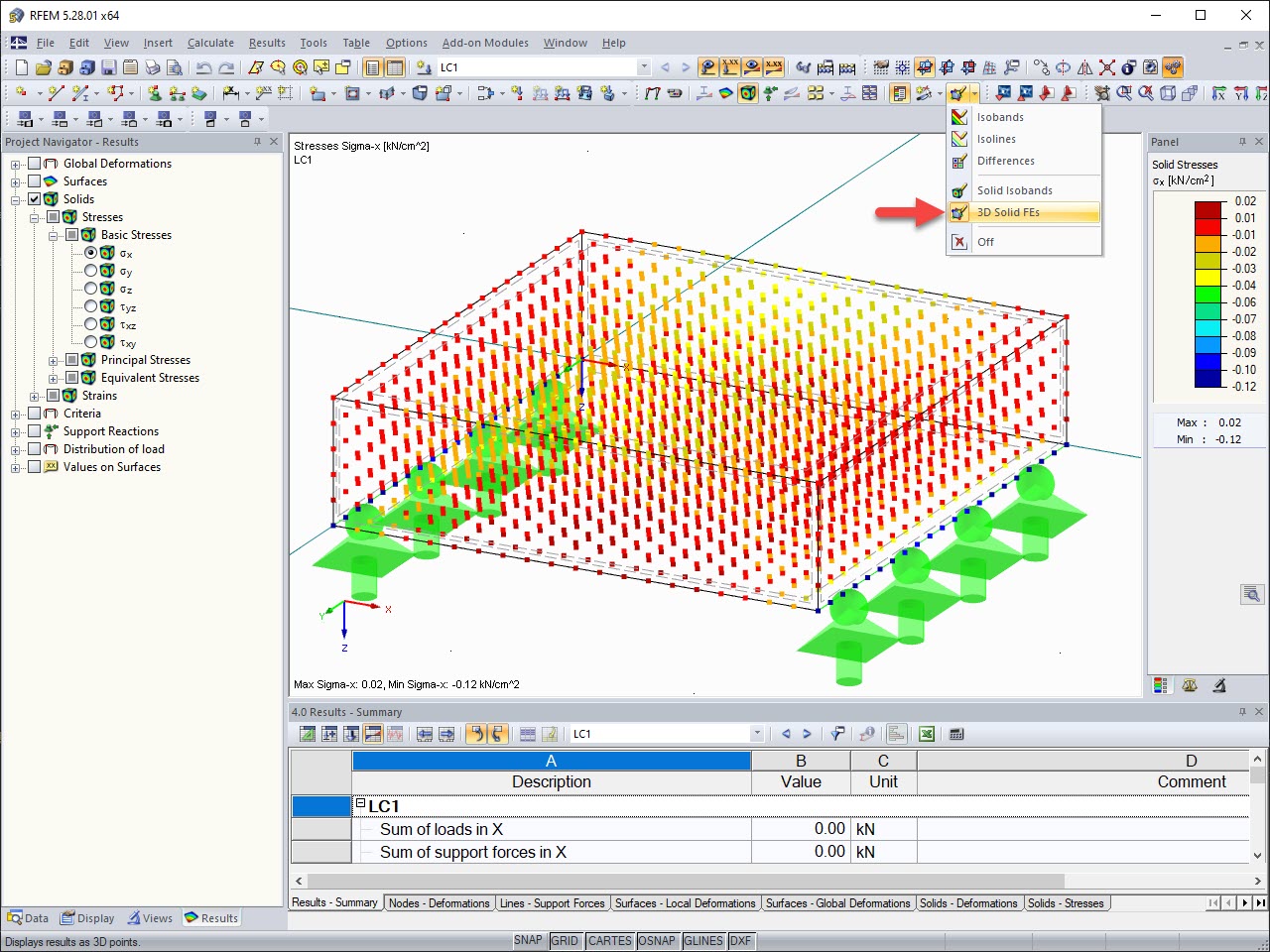
Shear Forces of Partial Cross-Section

The shear forces of the partial cross-section determined in SHAPE-THIN 8 are displayed in Image 03.

References

[1] Beck, H., & Schäfer, H. (1969). Die Berechnung von Hochhäusern durch Zusammenfassung aller aussteifenden Bauteile zu einem Balken. Der Bauingenieur, Heft 3.