基本
使用有限元法进行模拟是基于所谓的离散化。 未知解问题被分解成子问题，找到一个近似解。 这种计算方法是将几何图形分解成有限的组成部分，并通过形函数来近似描述其物理行为。 由此可见进行网格收敛研究的重要意义。 通常，有限元网格是从粗糙的网格开始，通过迭代方式进行细化的。 目的是选择一个能够提供足够精确结果的网格。 目的是找到一个折衷方案。 一方面，网格应该足够精细，以至于进一步的细化不会导致精度的进一步相关提高，另一方面，为了节省资源（计算时间/内存空间），网格应该尽可能的粗糙。 [SCHOOL.INSTITUTION] 达到收敛极限时；例如，各步之间的结果变化小于 1%，解是稳定的。 通常情况下，位移的收敛速度比应力和应变的收敛时间早。 选择一个专门的监测点很重要，因为网格的变化可能会导致有限元网格节点的坐标发生变化。 例如在 RFEM 中可以通过计算几何定义的节点或附加的面结果点进行计算。
您可以使用不同的网格设置来控制 RFEM 中的网格划分。 如果结果取决于局部网格，建议不要细化整个模型。 为此，RFEM 提供了对有限元网格进行细化的选项。
悬臂构件挠度示例
如前所述，关于变形收敛是最简单的方法。 下面是按照 Bernd Klein [1] 规范的示例，分析网格划分对悬臂梁末端位移的影响。 该模型包含一个 100 mm 长的铝合金悬臂梁，弹性模量为 70 GPa。 截面是一个高 20mm，宽 1mm 的直立板。 在悬臂梁的末端施加 1 kN 荷载。
这里的目的是检查悬臂梁末端的变形，该悬臂梁末端是根据网格密度通过面建模的。 此外，还分析了三角形和四边形单元的不同类型的网格划分。 Zum Vergleich erfolgte die Modellierung ebenfalls mittels Balkenelementen, mit (Timoshenko) und ohne Berücksichtigung der Schubverzerrung (Bernoulli). 该模型包含四边形单元和四边形单元，以及计算结果如下图所示。
从图中可以看出，这种情况下梁单元的网格对末端节点的变形没有影响。 如预期的那样考虑剪切应变。 使用 7.145 mm，不考虑剪切畸变的变形（伯努利）小于根据 Timoshenko 的 7.365 mm。 随着网格细化的增加，悬臂梁面的变形接近该值。 下图可以清楚地看到这些关系。
板的应力和应变示例
在下一个例子中将展示网格划分对应力计算和应变的影响。 为此，建模了一个面有自由矩形荷载和吊装线支座。
在位于自由矩形荷载的一个角上的面结果点处检查网格收敛。 下图对此进行了说明。 上面上面的窗口显示模型，中间的窗口显示第一主应力，下面的窗口显示第一主应变。 模型中网格划分从左到右增加。
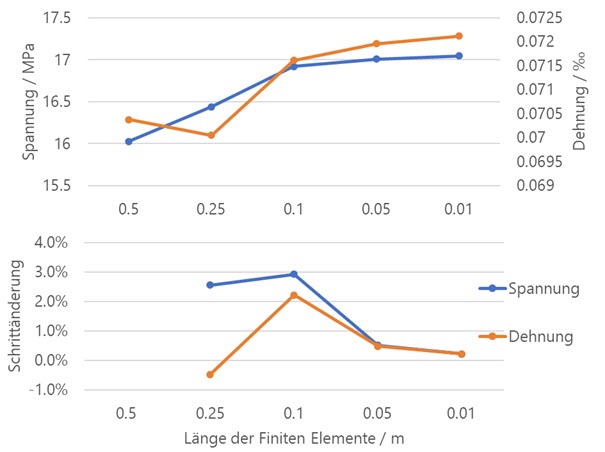
下图显示了应力和应变值如何通过增加网格细化来逼近极限值，即所谓的收敛行为。 因为无法轻松确定应力的实际值，所以可以评估与上一步网格划分步骤相比的相对变化。 这显示在图的下部。 将有限元单元的目标长度设置为 0.01 m，与上一次细化步骤相比，应力和应变仅相差约 0.2%
最终说明
下面的示例是对网格收敛分析的简化步骤。 但是要注意，在个别模拟中，计算的对象也可以是其他参数。 此外，各种因素可能导致计算书的要求有变化。 例如，它们可以是几何性质的，其中曲率应该由单元非常精确地表示。 与塑性分析相比，局部损伤分析（例如脆性破坏）需要更精细的网格。
随着网格细化的增加，网格没有逼近极限值，就会出现奇异性问题。 可以在以下技术文章中找到更多相关信息。
..png?mw=320&hash=bd2e7071b02d74aef6228d22c4b83867d2d7e1a5)
-gigapixel-standard_v2-2x.jpg?mw=350&hash=9166b062b07ae89e60417bff40b33fe9043f9d5e){kind=tracking}
.png?mw=600&hash=49b6a289915d28aa461360f7308b092631b1446e)