Generalidades
Las simulaciones realizadas mediante el método de los elementos finitos se basan en la denominada discretización. En este proceso, un problema con solución desconocida se descompone en subproblemas para los que puede determinarse una solución aproximada. En el caso que nos ocupa, esto afecta a una discretización geométrica en componentes finitos (elementos), cuyo comportamiento físico puede describirse aproximadamente mediante funciones de aproximación. De ello se desprende la relevancia de realizar un estudio de convergencia de malla. Por norma general, la malla de EF se refina iterativamente partiendo de una malla gruesa. El objetivo es elegir una malla que proporcione resultados suficientemente precisos. Para ello se busca un punto medio. La malla debe ser, por un lado, lo suficientemente fina como para que un refinamiento adicional no implique una mejora relevante adicional de la precisión, pero por otro lado lo más gruesa posible para ahorrar recursos (tiempo de cálculo/espacio de memoria). Alcanzar el límite de convergencia, por ejemplo, menos del 1 % de variación de los resultados entre los pasos, indica una solución estable. En general, la convergencia suele alcanzarse antes en desplazamientos que en resultados de orden superior, como tensiones y deformaciones. Es importante elegir un punto concreto de control, ya que la modificación de la malla también puede provocar un cambio en las coordenadas de los nudos de la malla EF. En RFEM, esto puede lograrse, por ejemplo, evaluando en nudos definidos geométricamente o mediante puntos de resultados de superficies adicionales.
En RFEM puede controlar la malla mediante diversos ajustes de malla. Asimismo, si se produce una dependencia local de los resultados respecto a la malla, puede ser recomendable no refinar todo el modelo. Para ello, RFEM ofrece la posibilidad de una densificación local de la malla de EF.
Ejemplo de deformación en una viga en voladizo
Como ya se ha mencionado, la obtención de la convergencia respecto a las deformaciones es la más sencilla. A continuación se muestra un ejemplo según Bernd Klein [1], que examina la influencia de la malla en el desplazamiento final de una viga en voladizo. El modelo consiste en una viga en voladizo de aluminio de 100 mm de longitud con un módulo de elasticidad de 70 GPa. La sección es una chapa plana vertical con 20 mm de altura y 1 mm de ancho. Se aplica una carga de 1 kN en el extremo de la viga en voladizo.
El objetivo es comprobar la deformación en el extremo de la viga en voladizo, modelada mediante superficies, en función de la densidad de malla. Además, se han analizado diferentes tipos de malla, elementos triangulares y cuadrangulares. A modo de comparación, el modelado también se realizó mediante elementos de barra, con consideración de la deformación por cortante (Timoshenko) y sin ella (Bernoulli). El modelo de los elementos de barra y cuadrangulares, así como los resultados obtenidos, se muestran en la siguiente figura.
Como puede verse, en este caso la malla del elemento de barra no tiene influencia sobre la deformación del nudo final. Sí la tiene, como era de esperar, la consideración de la deformación por cortante. La deformación sin deformación por cortante (Bernoulli) es de 7,145 mm y, por tanto, menor que la de Timoshenko, de 7,365 mm. Las deformaciones de las superficies de la viga en voladizo se aproximan a este valor a medida que aumenta la finura de la malla. Estas relaciones se aprecian claramente en el siguiente diagrama.
Ejemplo de tensión y deformación en una placa
El siguiente ejemplo pretende mostrar la influencia de la malla sobre los resultados calculados de tensiones y deformaciones. Para ello se modeló una superficie con carga rectangular libre y apoyos lineales desprendibles.
La convergencia de malla se comprueba en un punto de resultados de superficie en una esquina de la carga rectangular libre. La siguiente figura lo ilustra. La ventana superior muestra el modelo con malla, la central las primeras tensiones principales obtenidas y la inferior las primeras deformaciones principales. La malla aumenta en los modelos de izquierda a derecha.
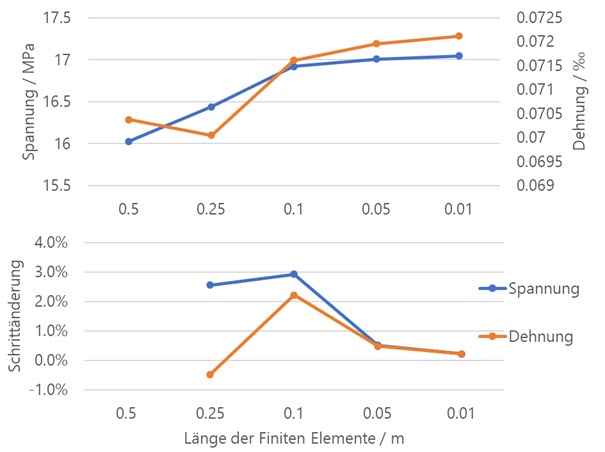
El siguiente diagrama muestra las aproximaciones de los valores de tensión y deformación, a medida que aumenta la finura de malla, a un valor límite, el denominado comportamiento de convergencia. Dado que aquí el valor real de la tensión no es trivial de determinar, resulta adecuado evaluar el cambio relativo respecto al paso de refinamiento anterior. Esto se muestra en la parte inferior del diagrama. Con una longitud objetivo de los elementos de EF de 0,01 m, tanto la tensión como la deformación solo se desvían en torno a un 0,2 % del paso de refinamiento anterior
Ejemplo de análisis lineal de pandeo de una carcasa cilíndrica
Al determinar los autovalores también cabe esperar una influencia no despreciable de la finura de la malla. Esto afecta, por un lado, al número de formas propias, que depende directamente de los grados de libertad. Por otro lado, también son relevantes los efectos locales de rigidización y la distribución de los puntos de masa. Por ello, también debe realizarse una convergencia de malla para el análisis de estabilidad y las simulaciones dinámicas, en particular los análisis modales.
El siguiente ejemplo está inspirado en un artículo de Łukasz Skotny Ph.D. [2] y fue publicado por primera vez por Ondřej Švorc en LinkedIn. El modelo consiste en una carcasa cilíndrica de aluminio de 0,2 m de altura y 2 mm de espesor (EN AW-3004 H14) con un diámetro de 0,1 m. Las superficies superior e inferior están ejecutadas mediante superficies rígidas y cargadas con 1 kN, respectivamente apoyadas de forma inmóvil. Mediante un refinamiento sucesivo de la malla de 15 mm a 3 mm se examina la influencia de la finura de malla sobre la carga crítica de bifurcación del análisis lineal de pandeo.
En la siguiente imagen se muestran los resultados del análisis de pandeo para una longitud de malla de EF de 15, 6 y 3 mm con la malla deformada.
La carga ideal de bifurcación también puede determinarse analíticamente para este caso según EN 1999-1-5, basándose en la teoría clásica de cascarones según Lorenz/Timoshenko/Southwell. La determinación para un cilindro largo, con comprobación de la esbeltez límite, se muestra en la siguiente fórmula:
En el estudio de convergencia de malla se observó que la carga crítica de bifurcación disminuye a medida que aumenta la finura de la malla y se aproxima a un valor límite. El siguiente diagrama muestra la carga crítica de bifurcación en función del número de elementos (izquierda) o de su valor recíproco (derecha). La malla más gruesa (15 mm) sobreestima así la carga crítica de bifurcación en alrededor de un 25,5 %. La carga crítica de bifurcación de la malla más fina es de 1008 kN y, por tanto, aproximadamente un 5,3 % inferior a la determinada analíticamente. Las posibles razones de ello son la influencia de las condiciones de contorno, así como el comportamiento de rigidez de los elementos de cascarón implementados en RFEM.
En la siguiente figura se representa la desviación de la carga crítica de bifurcación respecto al resultado de la malla más fina analizada en función del tiempo de cálculo (izquierda) o del tamaño de malla (derecha). A partir de un tamaño de malla de 5 mm, el cambio relativo respecto al siguiente paso más grueso es inferior al 2 %, al igual que respecto al resultado de la malla más fina (3 mm). El tiempo de cálculo, en cambio, casi se triplica, pasando de unos 11 a 30 s. Esta relación muestra claramente el compromiso entre tiempo de cálculo y precisión, típico de las simulaciones de EF.
Para este ejemplo también pueden encontrarse valores límite analíticos y normativos para la finura de malla. Según la EN 1993-1-6:2007, anexo §C.3, debe realizarse un estudio de convergencia con al menos 3 niveles de malla y un factor de refinamiento mayor o igual a 1,5. El criterio de convergencia es aquí una variación del αcr menor o igual al 1 % entre los dos últimos niveles. Según la prEN 1993-1-14 §4, actualmente todavía no introducida, la malla debe ser capaz de resolver la forma de fallo determinante. En los análisis de pandeo, esta es la longitud de onda crítica de pandeo. Para una buena resolución, pueden considerarse aquí 4 elementos como suficientes. El tamaño de malla resulta así para esta geometría de unos 4 mm. Lo cual coincide también con los resultados del estudio de convergencia realizado aquí (variación relativa ~ 1 %).
Para este caso también cabe señalar que una malla demasiado fina no es automáticamente mejor. Con elementos muy pequeños aumenta el número de condicionamiento de la matriz de rigidez, lo que puede favorecer imprecisiones numéricas en el solucionador de autovalores (Lanczos, iteración en subespacio). El valor óptimo se sitúa, con una forma de pandeo claramente definida, en un tamaño de malla de unos 3,5 mm.
Observaciones finales
Los ejemplos elegidos aquí pretenden mostrar un procedimiento simplificado para el estudio de la convergencia de malla. Sin embargo, debe tenerse en cuenta que en una simulación individual otros parámetros característicos pueden ser el objetivo de este estudio. Además, distintos factores pueden dar lugar a diferentes requisitos. Estos pueden ser, por ejemplo, de naturaleza geométrica, cuando una curvatura debe representarse con gran precisión mediante los elementos. Asimismo, el estudio de daños locales (p. ej., comportamiento de rotura frágil) requiere una malla comparativamente más fina que en el caso de la plastificación.
Si con una mayor finura de malla no se alcanza una aproximación a un valor límite, podría tratarse de una singularidad. Encontrará más información al respecto en el artículo técnico en el siguiente enlace.