Ogólne
Symulacje przeprowadzane metodą elementów skończonych opierają się na tzw. dyskretyzacji. W jej ramach problem o nieznanym rozwiązaniu dzieli się na podproblemy, dla których można wyznaczyć rozwiązanie przybliżone. W omawianym tutaj przypadku dotyczy to geometrycznego podziału na skończone (finite) elementy, których zachowanie fizyczne można w przybliżeniu opisać za pomocą funkcji kształtu. Z tego wynika znaczenie przeprowadzenia badania zbieżności siatki. Zazwyczaj siatka MES jest iteracyjnie zagęszczana, zaczynając od siatki zgrubnej. Celem takiego postępowania jest wybór siatki, która zapewnia wystarczająco dokładne wyniki. Dąży się przy tym do kompromisu. Siatka powinna być z jednej strony na tyle drobna, aby dalsze zagęszczenie nie powodowało już istotnego wzrostu dokładności, z drugiej zaś możliwie zgrubna, aby oszczędzać zasoby (czas obliczeń/miejsce w pamięci). Osiągnięcie granicy zbieżności, np. mniej niż 1% zmiany wyników między krokami, wskazuje na stabilne rozwiązanie. Ogólnie przyjmuje się, że zbieżność jest osiągana łatwiej dla przemieszczeń niż dla wyników wyższego rzędu, takich jak naprężenia i odkształcenia. Ważne jest przy tym wybranie konkretnego punktu do monitorowania, ponieważ zmiana siatki może również powodować zmianę współrzędnych węzłów siatki MES. W RFEM można to uzyskać na przykład poprzez analizę w zdefiniowanych geometrycznie węzłach lub przez dodatkowe punkty wyników powierzchni.
Siatką w RFEM można sterować za pomocą różnych ustawień siatki. Możliwe jest również, aby w przypadku lokalnej zależności wyników od siatki nie zagęszczać całego modelu. W tym celu RFEM oferuje możliwość lokalnego zagęszczania siatki MES.
Przykład: odkształcenie wspornika
Jak już wspomniano, uzyskanie zbieżności w odniesieniu do odkształceń jest najprostsze. Poniżej przedstawiono przykład według Bernda Kleina [1], który bada wpływ siatki na przemieszczenie końcowe wspornika. Model składa się ze wspornika aluminiowego o długości 100 mm i module sprężystości 70 GPa. Przekrój stanowi płaska, stojąca blacha o wysokości 20 mm i szerokości 1 mm. Na końcu wspornika przyłożono obciążenie 1 kN.
Celem jest tutaj sprawdzenie odkształcenia na końcu wspornika, modelowanego za pomocą powierzchni, w zależności od gęstości siatki. Dodatkowo zbadano różne rodzaje siatki: elementy trójkątne i czworokątne. Dla porównania modelowano również za pomocą elementów prętowych, z uwzględnieniem (Timoshenko) i bez uwzględnienia odkształcenia postaciowego (Bernoulli). Model elementów prętowych i czworokątnych oraz uzyskane wyniki przedstawiono na poniższym rysunku.
Jak widać, w tym przypadku siatka elementów prętowych nie ma wpływu na odkształcenie węzła końcowego. Natomiast zgodnie z oczekiwaniami wpływ ma uwzględnienie odkształcenia postaciowego. Ugięcie bez odkształcenia postaciowego (Bernoulli) wynosi 7,145 mm i jest mniejsze niż według Timoshenki, gdzie wynosi 7,365 mm. Ugięcia powierzchni wspornika zbliżają się do tej wartości wraz ze wzrostem dokładności siatki. Zależności te dobrze pokazano na poniższym wykresie.
Przykład: naprężenia i odkształcenia na płycie
Następny przykład ma pokazać wpływ siatki na obliczone wyniki naprężeń i odkształceń. W tym celu zamodelowano powierzchnię z wolnym obciążeniem prostokątnym i podporami liniowymi zapobiegającymi unoszeniu.
Zbieżność siatki sprawdzono w punkcie wynikowym powierzchni w narożu wolnego obciążenia prostokątnego. Poniższy rysunek ma to zilustrować. Górne okno pokazuje model z siatką, środkowe uzyskane pierwsze naprężenia główne, a dolne pierwsze odkształcenia główne. Gęstość siatki w modelach rośnie z lewej do prawej strony.
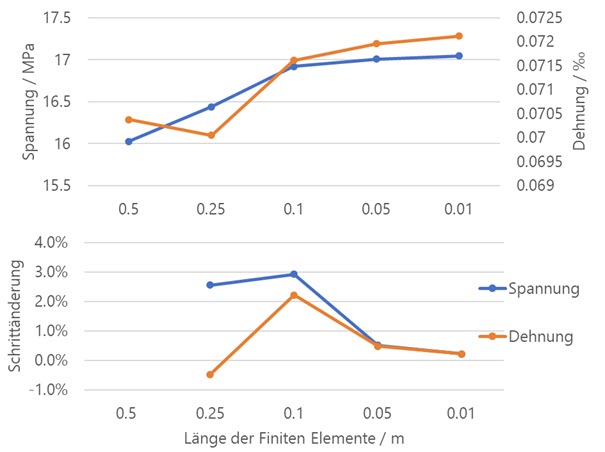
Poniższy wykres pokazuje zbliżanie się wartości naprężeń i odkształceń wraz ze wzrostem dokładności siatki do wartości granicznej, tzw. zachowanie zbieżności. Ponieważ rzeczywistej wartości naprężenia nie da się tutaj łatwo wyznaczyć, korzystne jest określenie względnej zmiany w odniesieniu do poprzedniego kroku zagęszczenia siatki. Przedstawiono to w dolnej części wykresu. Przy docelowej długości elementów MES wynoszącej 0,01 m zarówno naprężenie, jak i odkształcenie różnią się od poprzedniego kroku zagęszczenia już tylko o około 0,2%
Przykład: liniowa analiza wyboczeniowa powłoki cylindrycznej
Przy wyznaczaniu wartości własnych również można oczekiwać istotnego wpływu dokładności siatki. Dotyczy to z jednej strony liczby postaci własnych, która bezpośrednio zależy od liczby stopni swobody. Z drugiej strony istotne są także lokalne efekty usztywniające oraz rozmieszczenie punktów masowych. Dlatego również w przypadku analiz stateczności i symulacji dynamicznych, w szczególności analiz modalnych, należy przeprowadzić badanie zbieżności siatki.
Poniższy przykład jest inspirowany artykułem Łukasza Skotnego Ph.D. [2] i został po raz pierwszy opublikowany przez Ondřeja Švorca na LinkedIn. Model składa się z aluminiowej powłoki cylindrycznej EN AW-3004 H14 o wysokości 0,2 m i grubości 2 mm, o średnicy 0,1 m. Górna i dolna powierzchnia są wykonane jako powierzchnie sztywne i obciążone siłą 1 kN, względnie zamocowane bez przemieszczeń. Poprzez stopniowe zagęszczanie siatki z 15 mm do 3 mm badany jest wpływ dokładności siatki na krytyczne obciążenie bifurkacyjne w liniowej analizie wyboczeniowej.
Na poniższym obrazie przedstawiono wyniki analizy wyboczeniowej dla długości elementu MES 15, 6 i 3 mm z odkształconą siatką.
Idealne obciążenie bifurkacyjne można w tym przypadku również wyznaczyć analitycznie zgodnie z EN 1999-1-5, na podstawie klasycznej teorii powłok według Lorenza/Timoshenki/Southwella. Wyznaczenie dla długiego cylindra, z uwzględnieniem sprawdzenia smukłości granicznej, pokazano w poniższym wzorze:
Badanie zbieżności siatki wykazało, że krytyczne obciążenie bifurkacyjne maleje wraz ze wzrostem dokładności siatki i zbliża się do wartości granicznej. Poniższy wykres pokazuje krytyczne obciążenie bifurkacyjne w zależności od liczby elementów (po lewej) oraz jej odwrotności (po prawej). Najgrubsza siatka (15 mm) zawyża więc krytyczne obciążenie bifurkacyjne o około 25,5 %. Krytyczne obciążenie bifurkacyjne dla najdrobniejszej siatki wynosi 1008 kN, a więc jest o około 5,3 % niższe od wartości wyznaczonej analitycznie. Możliwe przyczyny tego to wpływ warunków brzegowych oraz zachowanie sztywności elementów powłokowych zaimplementowanych w RFEM.
Na następnym rysunku przedstawiono odchylenie krytycznego obciążenia bifurkacyjnego od wyniku dla najdrobniejszej badanej siatki w zależności od czasu obliczeń (po lewej) oraz rozmiaru siatki (po prawej). Dla rozmiaru siatki 5 mm względna zmiana względem następnego, grubszego kroku wynosi poniżej 2 %, podobnie jak względem wyniku najdrobniejszej siatki (3 mm). Czas obliczeń natomiast prawie się potraja, z około 11 do 30 s. Zależność ta dobrze pokazuje kompromis między czasem obliczeń a dokładnością, typowy dla symulacji MES.
Dla tego przykładu można również znaleźć analityczne i normowe wartości graniczne dotyczące dokładności siatki. Zgodnie z EN 1993-1-6:2007, załącznik §C.3, należy przeprowadzić badanie zbieżności z co najmniej 3 poziomami siatki i współczynnikiem zagęszczenia większym lub równym 1,5. Kryterium zbieżności stanowi tutaj zmiana αcr mniejsza lub równa 1 % między dwoma ostatnimi poziomami. Zgodnie z jeszcze nie wprowadzoną normą prEN 1993-1-14 §4 siatka musi być w stanie odwzorować decydującą formę zniszczenia. W przypadku analiz wyboczeniowych jest to krytyczna półfala wyboczeniowa. Dla dobrego odwzorowania można przyjąć, że wystarczą tu 4 elementy. Rozmiar siatki dla tej geometrii wynosi więc około 4 mm. Jest to zgodne z wynikami przeprowadzonego tutaj badania zbieżności (względna zmiana ~ 1 %).
Należy również zauważyć, że zbyt drobna siatka nie jest automatycznie lepsza. Przy bardzo małych elementach rośnie liczba uwarunkowania macierzy sztywności, co może sprzyjać numerycznym niedokładnościom w solverze wartości własnych (Lanczos, iteracja w podprzestrzeni). Wartość optymalna wynosi dla wyraźnie odwzorowanej postaci wyboczeniowej około 3,5 mm.
Uwagi końcowe
Wybrane tutaj przykłady mają pokazać uproszczone postępowanie przy badaniu zbieżności siatki. Należy jednak pamiętać, że w indywidualnej symulacji innym wielkościom charakterystycznym może przypadać rola celu tego badania. Ponadto różne czynniki mogą prowadzić do zmienionych wymagań. Mogą one mieć na przykład charakter geometryczny, gdy krzywizna ma być bardzo dokładnie odwzorowana przez elementy. Również analiza lokalnych uszkodzeń (np. kruchego pękania) wymaga porównywalnie drobniejszej siatki niż przy uplastycznieniu.
Jeśli przy rosnącej dokładności siatki nie następuje zbliżanie się do wartości granicznej, może to oznaczać osobliwość. Dalsze informacje na ten temat można znaleźć w artykule specjalistycznym pod poniższym linkiem.