Obecné
Simulace prováděné metodou konečných prvků jsou založeny na takzvané diskretizaci. Úloha s neznámým řešením se rozloží na dílčí problémy, pro které lze stanovit přibližné řešení. V našem případě se jedná o geometrický rozklad na konečné složky (prvky), jejichž fyzikální chování lze přibližně popsat pomocí tvarových funkcí. To ukazuje, jak je důležité provést studii konvergence sítě. Obvykle se síť KP zjemňuje iteračně, přičemž se vychází z hrubé sítě. Cílem je vybrat síť, která poskytuje dostatečně přesné výsledky. Cílem je najít střední cestu. Na jedné straně by síť měla být dostatečně jemná, aby dodatečné zjemnění nevedla k dalšímu významnému zvýšení přesnosti, na druhé straně by však měla být co nejhrubší, aby se šetřily zdroje (čas výpočtu/paměťový prostor). Při dosažení mezní hodnoty konvergence; například při změně výsledků mezi kroky menší než 1% je řešení stabilní. Obecně zde platí, že u posunů je konvergence dosaženo dříve než u hodnot s vysokou hodnotou, jako jsou napětí a přetvoření. Pro sledování je důležité vybrat vyhrazený bod, protože změna sítě může vést také ke změně souřadnic uzlů sítě konečných prvků. Toho lze v programu RFEM provést například vyhodnocením na geometricky definovaných uzlech nebo na dalších výsledkových bodech plochy.
Síťování lze v programu RFEM nastavit pomocí různých nastavení. Pokud výsledky závisí na lokální síti, může být vhodné nezjemňovat celý model. Pro tento účel nabízí RFEM možnost lokálního zahuštění sítě konečných prvků.
Příklad průhybu na konzole
Jak jsme již zmínili, nejjednodušší je dosáhnout konvergence s ohledem na deformace. Níže uvádíme příklad podle Bernda Kleina [1], který analyzuje vliv síťování na posun konce konzoly. Model se skládá ze 100 mm dlouhé hliníkové konzoly s modulem pružnosti 70 GPa. Průřez je rovná svislá deska o výšce 20 mm a šířce 1 mm. Na konec konzoly působí zatížení 1 kN.
Cílem je zkontrolovat deformaci na konci konzoly, která byla modelována pomocí ploch, v závislosti na hustotě sítě. Kromě toho byly analyzovány různé typy sítí, trojúhelníkové a čtyřúhelníkové prvky. Pro srovnání bylo provedeno modelování také pomocí prutových prvků s (Timošenkovou) a bez zohlednění smykového přetvoření (Bernoulli). Model nosníků a čtyřúhelníků a získané výsledky jsou znázorněny na obrázku níže.
Jak je vidět, síť nosníkového prvku nemá v tomto případě žádný vliv na deformaci koncového uzlu. Smykové přetvoření je ovšem uvažováno podle očekávání. Deformace bez smykového přetvoření (Bernoulli) 7,145 mm je menší než podle Timošenka se 7,365 mm. Deformace konzolových ploch se blíží této hodnotě se zvyšujícím se zahuštěním sítě. Tyto vztahy jsou dobře patrné z následujícího diagramu.
Příklad napětí a přetvoření na desce
V následujícím příkladu si ukážeme vliv sítě prvků na vypočítané výsledky napětí a přetvoření. Za tímto účelem byla modelována plocha s volným obdélníkovým zatížením a zvedajícími se liniovými podporami.
Konvergence sítě se kontroluje ve výsledkovém bodě plochy, který se nachází v rohu volného obdélníkového zatížení. Následující obrázek ilustruje tento princip. V horním okně se zobrazí model se síťováním, v prostředním okně se zobrazí získaná první hlavní napětí a v dolním okně se zobrazí první hlavní přetvoření. Síťování se v modelech zjemňuje zleva doprava.
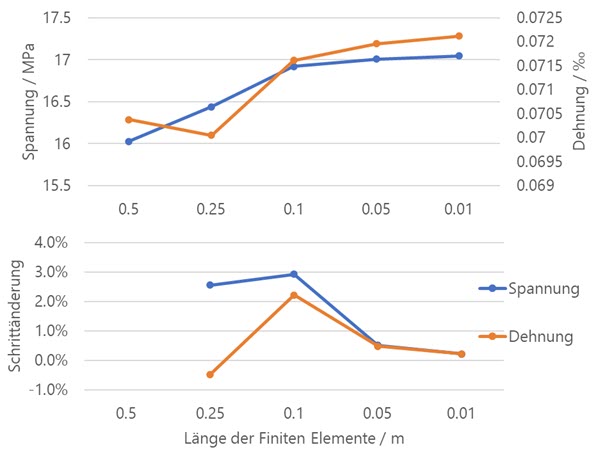
Následující diagram ukazuje, jak jsou hodnoty napětí a deformace aproximovány mezními hodnotami pomocí rostoucího zjemnění sítě, takzvaného konvergenčního chování. Vzhledem k tomu, že skutečnou hodnotu napětí nelze triviálně stanovit, je možné vyhodnotit relativní změnu ve srovnání s předchozím krokem tvorby sítě. To je znázorněno ve spodní části diagramu. Při požadované délce konečných prvků 0,01 m se napětí i přetvoření liší pouze asi o 0,2 % od předchozího kroku zjemnění
Závěrečné poznámky
Zde vybrané příklady ukazují zjednodušený postup pro analýzu konvergence sítě. Je však třeba poznamenat, že v individuální simulaci mohou být cílem této analýzy další parametry. Kromě toho mohou různé faktory vést ke změně požadavků. Mohou být například geometrického charakteru, přičemž zakřivení by mělo být velmi přesně znázorněno prvky. Také analýza lokálního poškození (např. chování při křehkém porušení) vyžaduje poměrně jemnější síť než pro plastifikaci.
Pokud se síť při rostoucím zahuštění sítě nepřiblíží mezní hodnotě, může se jednat o problém singularity. Další informace k tomu najdete v odborném článku pod následujícím odkazem.