Généralités
Les simulations réalisées à l'aide de la méthode des éléments finis reposent sur la discrétisation. Dans ce processus, un problème avec une solution inconnue est décomposé en sous-problèmes pour lesquels une solution approchée peut être déterminée. Dans le cas présent, cela concerne une décomposition géométrique en composants finis (éléments) dont le comportement physique peut être approximativement décrit par des fonctions d'approche. Cela souligne l'importance de mener une étude de convergence de maillage. Généralement, le maillage EF est affiné itérativement à partir d'un maillage grossier.
L'objectif est de choisir un maillage qui fournit des résultats suffisamment précis. Un compromis est recherché, de sorte que le maillage soit suffisamment fin pour qu'une raffinement supplémentaire n'entraîne pas d'amélioration significative de la précision, mais reste aussi grossier que possible pour préserver les ressources (temps de calcul/espace mémoire).
Atteindre la limite de convergence, par exemple moins de 1% de changement dans les résultats entre les étapes, indique une solution stable. En général, la convergence pour les déplacements est atteinte plus facilement que pour des résultats de niveau supérieur, tels que les contraintes et les déformations. Il est important de choisir un point dédié à la surveillance, car le changement de maillage peut également conduire à un changement des coordonnées des nœuds du maillage EF. Vous pouvez réaliser cela dans RFEM, par exemple, en évaluant des nœuds définis géométriquement ou en utilisant des points de résultats de surface supplémentaires.
Vous pouvez contrôler le maillage dans RFEM grâce à divers paramètres de maillage. Il peut également être recommandé, en cas de dépendance locale des résultats par rapport au maillage, de ne pas affiner tout le modèle. Pour cela, RFEM offre la possibilité d'un raffinement local du maillage EF.
Exemple de déformation d’une porte-à-faux
Comme déjà mentionné, obtenir une convergence par rapport aux déformations est le plus simple. Ci-dessous se trouve un exemple basé sur Bernd Klein [1], qui examine l'influence du maillage sur le déplacement final d'un porte-à-faux. Le modèle se compose d’une porte-à-faux de 100 mm de long en aluminium avec un module d’élasticité de 70 GPa. La section transversale est une plaque plate verticale de 20 mm de hauteur et 1 mm de largeur. Une charge de 1 kN est appliquée à l'extrémité du porte-à-faux.
L'objectif est de vérifier la déformation à l'extrémité du porte-à-faux, qui a été modélisée à l'aide de surfaces, en fonction de la densité de maillage. Différents types de maillage, éléments triangulaires et quadrangulaires, ont été étudiés. Pour comparaison, la modélisation a également été effectuée à l'aide d'éléments poutres, avec (Timoshenko) et sans (Bernoulli) prise en compte de la distorsion de cisaillement. Le modèle des éléments poutres et quadrangulaires ainsi que les résultats obtenus sont illustrés dans l'image suivante.
Comme on peut le voir, dans ce cas, le maillage des éléments poutres n'affecte pas la déformation du nœud final. Cependant, la prise en compte de la distorsion de cisaillement le fait, comme on pouvait s'y attendre. La déformation sans distorsion de cisaillement (Bernoulli) est de 7,145 mm, inférieure à celle de Timoshenko avec 7,365 mm. Les déformations des surfaces du porte-à-faux se rapprochent de cette valeur à mesure que le maillage devient plus fin. Ces relations sont bien visibles dans le diagramme suivant.
Exemple de contrainte et de déformation sur une plaque
Le prochain exemple devrait montrer l'influence du maillage sur les résultats calculés en termes de contraintes et de déformations. Pour cela, une surface avec une charge rectangulaire libre et des supports de ligne en soulèvement a été modélisée.
La convergence du maillage est vérifiée à un point de résultat de surface dans un coin de la charge rectangulaire libre. L'image suivante illustre cela. La vue supérieure montre le modèle avec son maillage, celle du milieu montre les premières contraintes principales obtenues, et celle du bas les premières déformations principales. Le maillage s'intensifie de gauche à droite dans les modèles.
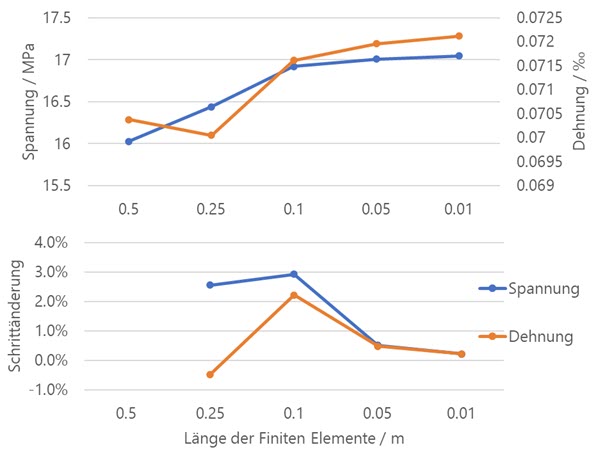
Le diagramme suivant montre les approximations des valeurs de contraintes et de déformations avec l'augmentation de la finesse du maillage vers une valeur limite, appelée comportement de convergence. Comme la valeur réelle de la contrainte n'est pas triviale à déterminer ici, l'évaluation du changement relatif par rapport à l'étape de maillage précédente est appropriée. Cela est illustré dans la partie inférieure du diagramme. Avec une longueur d'éléments EF ciblée de 0,01 m, les contraintes et les déformations ne s'écartent que d'environ 0,2% de l'étape de raffinement précédente.
Remarques finales
Les exemples choisis ici visent à montrer une approche simplifiée pour l'étude de la convergence de maillage. Cependant, il faut garder à l'esprit que dans la simulation individuelle, d'autres paramètres peuvent être l'objectif de cette étude. De plus, différents facteurs peuvent entraîner des exigences modifiées. Ceux-ci peuvent par exemple être d'ordre géométrique, lorsque une courbure doit être représentée très précisément par les éléments. De même, l'examen des dommages locaux (par exemple, comportement de rupture fragile) nécessite un maillage relativement plus fin qu'en cas de plastification.
Si avec l'augmentation de la finesse du maillage aucune convergence vers une limite n'est atteinte, il pourrait s'agir d'une singularité. Vous trouverez plus d'informations à ce sujet dans l'article technique au lien suivant.