Allgemeines
Simulationen, welche mithilfe der Finiten Elemente Methode durchgeführt werden, basieren auf der sogenannten Diskretisierung. Hierbei wird ein Problem mit unbekannter Lösung in Teilprobleme zerlegt, für welche eine Näherungslösung bestimmbar ist. In dem hier vorliegenden Fall betrifft dies eine geometrische Zerlegung in endliche (finite) Bestandteile (Elemente), deren physikalisches Verhalten über Ansatzfunktionen näherungsweise beschreibbar ist. Hieraus ergibt sich die Relevanz der Durchführung einer Netzkonvergenzstudie. Es wird im Normalfall das FE-Netz, von einer groben Vernetzung ausgehend, iterativ verfeinert. Ziel einer solchen ist es ein Netz zu wählen, welches hinreichend genaue Ergebnisse liefert. Hierbei wird ein Mittelweg angestrebt. Das Netz soll einerseits fein genug sein, dass eine zusätzliche Verfeinerung keine weitere relevante Genauigkeitssteigerung zur Folge hat, jedoch andererseits möglichst grob, um Ressourcen (Rechenzeit/Speicherplatz) zu schonen. Das Erreichen der Konvergenzgrenze, z.B. weniger als 1% Änderung der Ergebnisse zwischen den Schritten, weist auf eine stabile Lösung hin. Im Allgemeinen gilt hierbei, dass eine Konvergenz für Verschiebungen eher erreicht wird als bei höhewertigen Ergebnissen, wie Spannungen und Dehnungen. Wichtig ist hierbei, sich einen dezidierten Punkt für die Überwachung auszusuchen, da die Änderung der Vernetzung ebenfalls zur Änderung der Koordinaten von FE-Netz-Knoten führen kann. Dies können Sie in RFEM beispielsweise durch die Auswertung an geometrisch festgelegten Knoten oder über zusätzlichen Flächenergebnispunkte erreichen.
Die Vernetzung können Sie in RFEM über diverse Netz-Einstellungen steuern. Ebenfalls kann es empfehlenswert sein, wenn eine lokale Netzabhängigkeit der Ergebnisse auftritt, nicht das ganze Modell zu verfeinern. Hierfür bietet RFEM die Möglichkeit einer lokalen FE-Netzverdichtung.
Beispiel Verformung an Kragarm
Wie bereits erwähnt, ist die Herbeiführung einer Konvergenz bezüglich der Verformungen am einfachsten. Nachfolgend sehen Sie ein Beispiel nach Bernd Klein [1], welches den Vernetzungseinfluss für die Endverschiebung eines Kragarms untersucht. Das Modell besteht hierbei aus einem 100 mm langen Kragarm aus Aluminium mit einem Elastizitätsmodul von 70 GPa. Der Querschnitt ist ein flaches aufrecht stehendes Blech mit 20 mm Höhe und 1 mm Breite. Es wird eine Belastung von 1 kN am Ende des Kragarms aufgebracht.
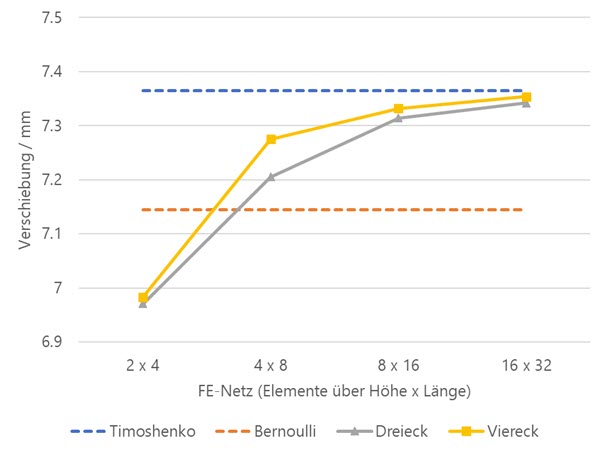
Ziel hierbei ist die Überprüfung der Verformung am Ende des Kragarms, welcher mittels Flächen modelliert wurde, abhängig von der Netzdichte. Zusätzlich wurden verschiedene Vernetzungsarten, Dreieck- und Viereckelemente, untersucht. Zum Vergleich erfolgte die Modellierung ebenfalls mittels Balkenelementen, mit (Timoshenko) und ohne Berücksichtigung der Schubverzerrung (Bernoulli). Das Modell der Balken- und Viereckselemente sowie die erhaltenen Ergebnisse sind in nachfolgender Abbildung dargestellt.
Wie man sehen kann, hat in diesem Fall die Vernetzung des Balkenelements keinen Einfluss auf die Verformung des Endknotens. Wohl jedoch erwartungsgemäß die Berücksichtigung der Schubverzerrung. Die Verformung ohne Schubverzerrung (Bernoulli) ist mit 7,145 mm geringer als nach Timoshenko mit 7,365 mm. Die Verformungen der Kragarmflächen nähern sich diesem Wert mit zunehmender Netzfeinheit an. Gut ersichtlich werden diese Zusammenhänge in nachfolgendem Diagramm.
Beispiel Spannung und Dehnung an Platte
Das nächste Beispiel soll den Vernetzungseinfluss auf die berechneten Spannung- und Dehnungsergebnisse zeigen. Hierfür wurde eine Fläche mit freier Rechtecklast und abhebenden Linienlagern modelliert.
Die Netzkonvergenz wird an einem Flächenergebnispunkt an einer Ecke der freien Rechtecklast überprüft. Nachfolgende Abbildung soll dies veranschaulichen. Das obere Fenster zeigt das Modell mit Vernetzung, das mittlere die erhaltenen ersten Hauptspannungen und das untere die der ersten Hauptdehnungen. Die Vernetzung nimmt bei den Modellen von links nach rechts zu.
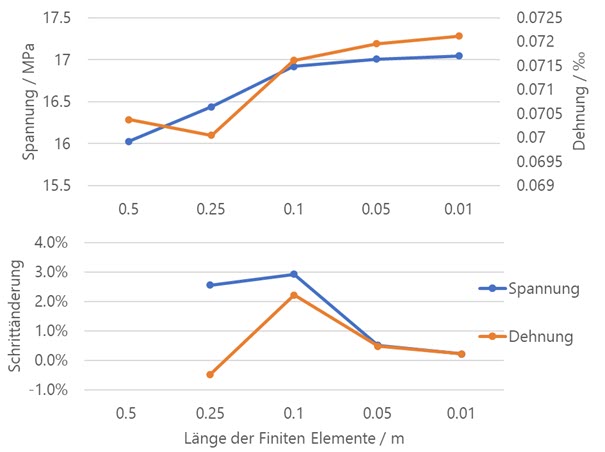
Das nachfolgende Diagramm zeigt die Annäherungen der Spannungs- und Dehnungswerte mit zunehmender Netzfeinheit an einen Grenzwert, das sogenannte Konvergenzverhalten. Da hier der tatsächliche Wert der Spannung nicht trivial zu ermitteln ist, bietet sich die Auswertung der relativen Änderung gegenüber dem vorangehenden Vernetzungsschritt an. Dies ist im unteren Teil des Diagramms dargestellt. Bei einer angestrebten Länge der FE-Elemente von 0,01 m weichen sowohl Spannung als auch Dehnung nur noch rund 0,2% vom vorangehenden Verfeinerungsschritt ab
Abschließende Anmerkungen
Die hier gewählten Beispiele sollen ein vereinfachtes Vorgehen für die Untersuchung der Netzkonvergenz zeigen. Es sollte jedoch bedacht werden, dass in der individuellen Simulation andere Kenngrößen Ziel dieser Untersuchung sein können. Des weiteren können unterschiedliche Faktoren zu geänderten Anforderungen führen. Diese können beispielsweise geometrischer Natur sein, in dem eine Krümmung sehr genau durch die Elemente abgebildet werden soll. Ebenfalls erfordert eine Untersuchung von lokalen Schädigungen (z.B. sprödes Bruchverhalten) eine vergleichsweise feinere Vernetzung als bei Plastzierung.
Falls bei zunehmender Netzfeinheit keine Annäherung an einen Grenzwert eintritt, könnte es sich um eine Singularität handeln. Weitere Informationen hierzu finden Sie in dem Fachbeitrag unter folgendem Link.