Общие сведения
Моделирование, выполняемое с помощью метода конечных элементов, основано на так называемой дискретизации. Проблема с неизвестным решением расщепляется на подпроблемы, для которых может быть найдено приближенное решение. В данном случае речь идет о геометрическом разложении на конечные компоненты (элементы), физические свойства которых можно приблизительно описать с помощью функций формы. Это показывает актуальность выполнения анализа сходимости сетки. Как правило, сетка КЭ детализируется итерационно, начиная с грубой сетки. Цель состоит в том, чтобы выбрать сетку, которая дает достаточно точные результаты. Главная цель состоит в том, чтобы найти золотую середину. С одной стороны, сетка должна быть достаточно мелкой, чтобы дополнительное измельчение не приводило к дальнейшему увеличению точности, но с другой стороны, она должна быть максимально грубой в целях сохранения ресурсов (время вычисления/пространство в памяти). При достижении предела сходимости; Например, изменение результатов между шагами менее чем на 1%, решение устойчиво. Как правило, в этом случае достигается сходимость для перемещений раньше, чем для результатов с высокими значениями, такими как напряжения и деформации. Важно выбрать для контроля специальную точку, потому что изменение сетки КЭ может привести к изменению координат узлов сетки КЭ. В программе RFEM это можно сделать, например, путем оценки геометрически заданных узлов или дополнительных точек результата поверхности.
Созданием сетки в программе RFEM можно управлять с помощью различных настроек сетки. Может быть целесообразно не уточнение всей модели, если результаты зависят от местной сетки. Для этого в программе RFEM предусмотрена возможность местного уплотнения сетки КЭ.
Пример прогиба на консоли
Как уже упоминалось, проще всего достичь сходимости по деформациям. Ниже приведен пример по Бернду Кляйну [1], в котором анализируется влияние сетки при перемещении конца консоли. Модель состоит из алюминиевой консоли длиной 100 мм с модулем упругости 70 ГПа. Сечение представляет собой плоский вертикальный лист высотой 20 мм и шириной 1 мм. На конец консоли действует нагрузка 1 кН.
Цель состоит в том, чтобы проверить деформацию на конце консоли, которая была смоделирована с помощью поверхностей, в зависимости от плотности сетки. Кроме того, были проанализированы различные типы сетки, треугольные и четырехугольные элементы. Для сравнения, моделирование было также выполнено с помощью балочных элементов, с учетом деформации сдвига (Тимошенко) и без учета деформации сдвига (Бернулли). Модель балки и четырехугольных элементов, а также полученные результаты показаны на рисунке ниже.
Как видно, в данном случае сетка балочного элемента не влияет на деформацию конечного узла. При этом деформация сдвига учитывается, как и ожидалось. При размере 7,145 мм деформация без искажения сдвига (Бернулли) меньше, чем по Тимошенко с 7,365 мм. Деформации поверхностей консоли приближаются к этому значению по мере измельчения сетки. Данные соотношения хорошо видны на следующей диаграмме.
Пример напряжения и деформации на плите
На следующем примере мы покажем влияние сетки на результаты расчетов напряжений и деформаций. Для этого была смоделирована поверхность со свободной прямоугольной нагрузкой и подъемными линейными опорами.
Сходимость сетки затем проверяется в результирующей точке поверхности, находящейся в углу произвольной прямоугольной нагрузки. Данный принцип хорошо показан на следующем рисунке. В верхнем окне показана модель с созданием сетки, в среднем окне - полученные первые главные напряжения, а в нижнем - первые главные деформации. Сетка увеличивается в моделях слева направо.
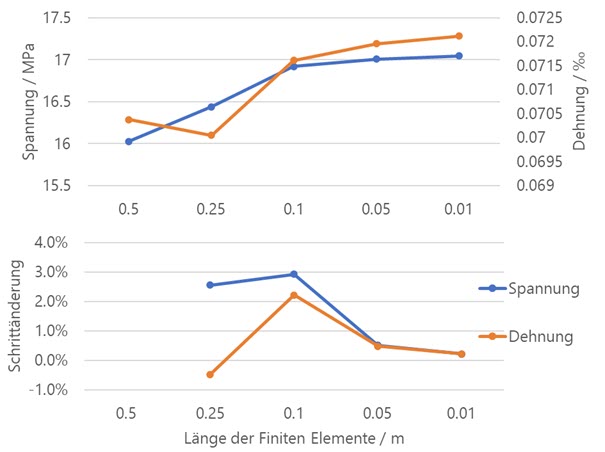
На следующей диаграмме затем показано, как значения напряжений и деформаций приближаются к предельному значению за счет увеличения измельчения сетки, так называемого поведения сходимости. Поскольку фактическое значение напряжения не может быть определено тривиально, можно оценить относительное изменение по сравнению с предыдущим шагом сетки. Это показано в нижней части диаграммы. При требуемой длине конечных элементов 0,01 м, как напряжение, так и деформация отличаются по сравнению с предыдущим шагом уточнения всего на 0,2%
Заключительные примечания
Выбранные примеры показывают упрощенный порядок расчета сходимости сетки. Тем не менее следует отметить, что в индивидуальном моделировании другие параметры могут быть целью данного анализа. Кроме того, различные факторы могут привести к изменению требований. Они могут иметь, например, геометрический характер, в котором кривизна должна быть очень точно представлена элементами. Кроме того, для расчета местных повреждений (например, работы при хрупком разрушении) требуется относительно более мелкая сетка, чем для расчета пластификации.
Если сетка не аппроксимируется к предельному значению при увеличении уплотнения сетки, это может быть проблемой сингулярности. Дополнительную информацию об этом можно найти в технической статье по следующей ссылке.