Generale
Le simulazioni eseguite utilizzando il metodo degli elementi finiti si basano su ciò che è noto come discretizzazione. Un problema con una soluzione sconosciuta è scomposto in sottoproblemi per i quali può essere determinata una soluzione approssimativa. Nel presente caso, si tratta di una scomposizione geometrica in componenti finite (elementi), il cui comportamento fisico può essere descritto approssimativamente da funzioni di forma. Questo mostra l'importanza di eseguire uno studio di convergenza della mesh. Di solito, la mesh EF viene raffinata iterativamente, a partire da una mesh approssimativa. L'obiettivo è selezionare una mesh che fornisca risultati sufficientemente accurati. L'obiettivo è trovare una via di mezzo. Da un lato, la mesh dovrebbe essere sufficientemente fine che un ulteriore perfezionamento non porti ad un ulteriore aumento rilevante della precisione, ma dall'altro, dovrebbe essere il più grossolana possibile al fine di risparmiare risorse (tempo di calcolo/spazio di memoria). Quando viene raggiunto il limite di convergenza; ad esempio, una variazione inferiore all'1% dei risultati tra i passaggi, la soluzione è stabile. In generale, qui accade che una convergenza per gli spostamenti viene raggiunta prima che per risultati di valore elevato, come tensioni e deformazioni. È importante scegliere un punto dedicato per il monitoraggio, perché la modifica della mesh può anche portare alla modifica delle coordinate dei nodi della mesh EF. È possibile farlo in RFEM, ad esempio, mediante la valutazione su nodi definiti geometricamente o su punti risultanti della superficie aggiuntivi.
È possibile controllare la mesh in RFEM utilizzando varie impostazioni della mesh. Potrebbe essere consigliabile non rifinire l'intero modello se i risultati dipendono dalla mesh locale. A tale scopo, RFEM offre l'opzione di infittimento della mesh EF locale.
Esempio di inflessione su uno sbalzo
Come già accennato, è più facile ottenere una convergenza per quanto riguarda gli spostamenti generalizzati. Di seguito è possibile vedere un esempio secondo Bernd Klein [1], che analizza l'influenza della mesh per lo spostamento finale di uno sbalzo. Il modello è costituito da uno sbalzo in alluminio lungo 100 mm con un modulo di elasticità di 70 GPa. La sezione trasversale è una lamiera piana eretta con un'altezza di 20 mm e una larghezza di 1 mm. Un carico di 1 kN è applicato alla fine dello sbalzo.
Lo scopo qui è quello di verificare la deformazione alla fine dello sbalzo, che è stato modellato per mezzo di superfici, a seconda della densità della mesh. Inoltre, sono stati analizzati vari tipi di mesh, elementi triangolari e quadrangolari. Per il confronto, la modellazione è stata eseguita anche utilizzando elementi trave, con (Timoshenko) e senza considerare la distorsione a taglio (Bernoulli). Il modello degli elementi trave e quadrangolare, nonché i risultati ottenuti, sono mostrati nella figura seguente.
Come si può vedere, la mesh dell'elemento trave in questo caso non ha influenza sulla deformazione del nodo finale. Tuttavia, la deformazione a taglio è considerata come prevista. Con 7,145 mm, la deformazione senza distorsione a taglio (Bernoulli) è inferiore rispetto a Timoshenko con 7,365 mm. Le deformazioni delle superfici a sbalzo si avvicinano a questo valore all'aumentare dell'infittimento della mesh. Queste relazioni sono chiaramente visibili nel diagramma seguente.
Esempio di tensione e deformazione su una piastra
Il prossimo esempio mostrerà l'influenza della mesh sui risultati di tensione e deformazione calcolati. Per questo, è stata modellata una superficie con un carico libero rettangolare e dei vincoli esterni delle linee di sollevamento.
La convergenza della mesh viene verificata in un punto risultante della superficie situato in un angolo del carico libero rettangolare. La figura seguente illustra questo principio. La finestra superiore mostra il modello con la mesh, la finestra centrale mostra le prime tensioni principali ottenute e quella inferiore mostra quelle delle prime deformazioni principali. La mesh aumenta nei modelli da sinistra a destra.
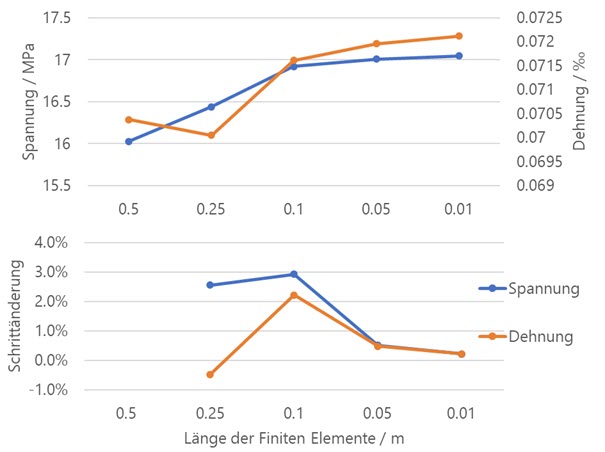
Il diagramma seguente mostra come i valori di tensione e deformazione sono approssimati a un valore limite dall'infittimento crescente della mesh, il cosiddetto comportamento di convergenza. Poiché il valore effettivo della tensione non può essere determinato banalmente, è possibile valutare la variazione relativa rispetto alla fase di meshing precedente. Questo è mostrato nella parte inferiore del diagramma. Con una lunghezza obiettivo degli elementi EF di 0,01 m, sia la tensione che la deformazione differiscono solo dello 0,2% circa dalla fase di affinamento precedente
Note finali
Gli esempi qui scelti mostrano una procedura semplificata per l'analisi della convergenza della mesh. Tuttavia, va notato che nella simulazione individuale, altri parametri possono essere l'obiettivo di questa analisi. Inoltre, vari fattori possono portare a requisiti modificati. Possono essere, ad esempio, di natura geometrica, in cui la curvatura dovrebbe essere rappresentata in modo molto preciso dagli elementi. Inoltre, l'analisi del danno locale (ad esempio, il comportamento a rottura fragile) richiede una mesh relativamente più fine rispetto alla plastificazione.
Se la mesh non viene approssimata a un valore limite nel caso di un infittimento della mesh crescente, questo potrebbe essere un problema di singolarità. È possibile trovare ulteriori informazioni al riguardo nell'articolo tecnico al seguente link.