Analisi diretta degli spostamenti generalizzati di una trave in cemento armato per quanto riguarda la viscosità e il ritiro

Questo articolo tecnico presenta un'analisi diretta delle deformazioni di una trave in cemento armato, considerando inoltre gli effetti a lungo termine della viscosità e del ritiro. Un esempio viene utilizzato per mostrare come questi effetti influenzano la deformazione di un componente strutturale e sono presi in considerazione nel calcolo. Spiega quali dati sono necessari in RFEM 6 per considerare correttamente tutti i fattori rilevanti e come il coefficiente di distribuzione influenza la rigidezza del componente strutturale.

Dati di input

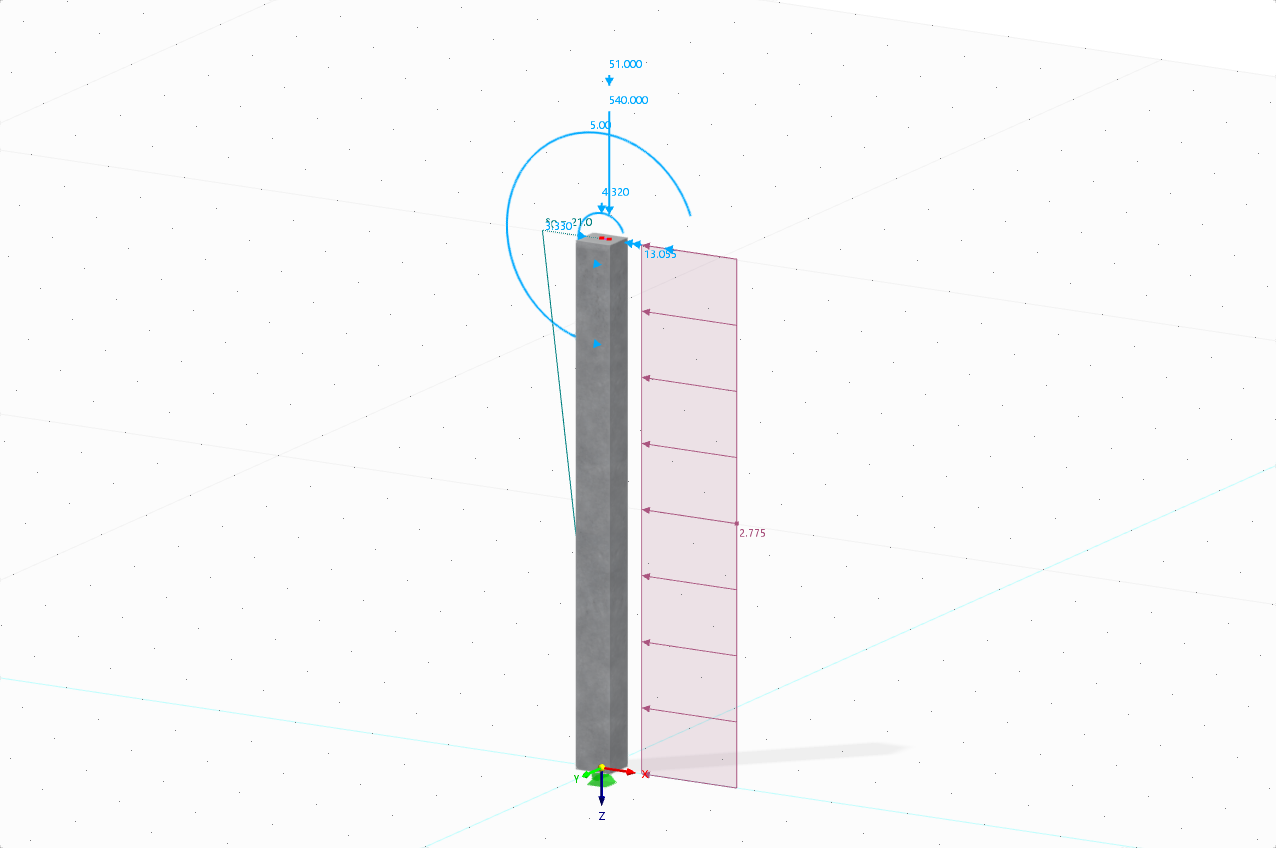
La geometria, l'armatura e il carico sono descritti dai seguenti parametri:

sistema

• Tipo trave: Trave a campata singola
• Lunghezza campata: l = 4.210 m

Sezione trasversale

• Spessore solaio: h = 20 cm
• Larghezza piastra b = 100 cm
• Materiale: Calcestruzzo C20/25 con E_cm = 30.000 MN/m² e B 500A
• Armatura: A_{s,-z,(inferiore)} = 4,45 cm² con 7 ∅ 9 e d₁ = 30 mm
• Altezza efficace dell'armatura inferiore: d_{def,+z (inferiore)} = 17 cm

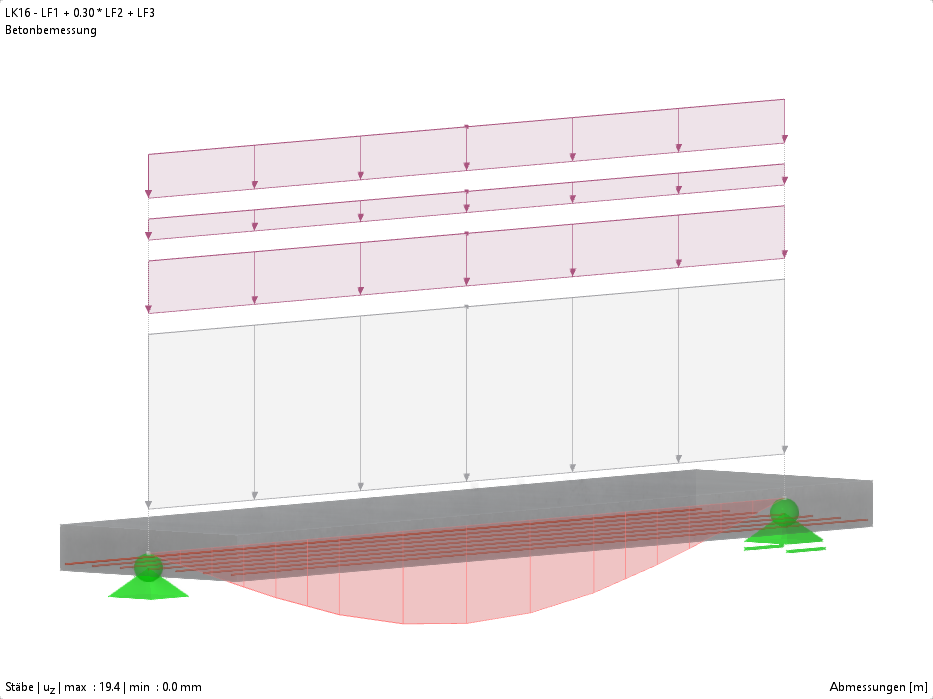
Carichi permanenti

• Peso proprio: g_s = 0,20 m ⋅ 1 m ⋅ 25 kN/m³ = 5,00 kN/m
• Intonaco e pavimentazione: g_bp = 1,50 kN/m
• Totale: g_k,totale = 6,5 kN/m

Carichi variabili

• Carico variabile (ufficio): q_b = 2,00 kN/m con ψ₂ = 0,3
• Compensazione della partizione: q_t = 1.25 kN/m con ψ₂ = 1.0

Carico quasi permanente

• 6,5 kN/m + 0,3 ⋅ 2,00 kN/m + 1,0 ⋅ 1,25 kN/m = 8,35 kN/m

Momento flettente di progetto per il calcolo dell'inflessione

• My_,Ed,def = 8,35 kN/m ⋅ (4,21 m)²/8 = 18,50 kNm

Valori iniziali dell'analisi degli spostamenti generalizzati

• Modulo di elasticità medio del calcestruzzo: E_cm = 30.000 MN/m²

• Rapporto di armatura longitudinale: ρ = A_s/A_c = 4,45 cm²/(20 cm ⋅ 100 cm) = 0,223%

• Deformazione da ritiro: ε_sh = -0,5 ‰
• Coefficiente di viscosità: φ = 2

È necessario attivare l'opzione "Proprietà avanzate del calcestruzzo" nelle impostazioni della sezione trasversale per specificare il coefficiente di viscosità tramite le impostazioni definite dall'utente.

Nella scheda ora disponibile, selezionare prima le opzioni "Viscosità" e "Ritiro" per visualizzare e modificare i "Valori di base delle proprietà dipendenti dal tempo". Il coefficiente di viscosità φ è stato specificato inserendo φ₀, ϵ_cd,0 e ϵ_ca(∞).

viscosità

Gli effetti di viscosità sono determinati da una riduzione del modulo di elasticità del calcestruzzo's E_c.

Il modulo di elasticità efficace E_c,eff tiene conto degli effetti a lungo termine del calcestruzzo, in particolare della viscosità. La viscosità descrive la deformazione a lungo termine del calcestruzzo sotto un carico costante. Il coefficiente di viscosità φ riduce il modulo di elasticità E_cm (modulo di elasticità medio del calcestruzzo) in modo che la rigidezza effettiva del calcestruzzo sia rappresentata per un lungo periodo di tempo. Questo valore viene utilizzato in ulteriori calcoli, come per il momento di inerzia o il rapporto di rigidezza.

E_c,eff = 30.000 MN/m²/( 1 + 2 ) = 10.001,2 MN/m²

Modulo di taglio efficace del calcestruzzo G_c,eff
Il modulo di taglio efficace descrive la resistenza del calcestruzzo's alle deformazioni a taglio ed è determinato con il rapporto tra la deformazione trasversale e la deformazione longitudinale (il rapporto di Poisson's v del calcestruzzo). Questo valore è particolarmente importante per il calcolo degli spostamenti generalizzati della sezione trasversale e per le verifiche di progetto a taglio.

G_c,eff = 10.001,2 MN/m²/( 2 ⋅ ( 1 + 0.2 ) ) = 4.167,180 MN/m²

Rapporto modulare efficace per stato non fessurato (carico di lunga durata) α_e,l
Il rapporto α_e,l indica quanto è più rigido l'acciaio rispetto al calcestruzzo sotto carico di lunga durata. E_s è il modulo di elasticità dell'acciaio, E_c,l è il modulo di elasticità efficace del calcestruzzo nello stato non fessurato (identico a E_c,eff ). Poiché il calcestruzzo ha una rigidezza inferiore a causa di effetti a lungo termine come la viscosità, il valore di α_e,l è più alto in questo stato. Questo rapporto viene utilizzato nel calcolo del baricentro e delle proprietà della sezione efficace.

α_e,l = 2 ⋅ 10⁵ MN/m²/10.001,2 MN/m² = 20

Rapporto modulare efficace per stato non fessurato (carico di breve durata) α_e,I,st
Il rapporto α_e,I,st descrive il rapporto tra la rigidezza dell'acciaio e del calcestruzzo sotto carico di breve durata. A differenza di α_e,l, qui viene utilizzato il modulo di elasticità medio E_cm senza considerare gli effetti di viscosità. Ciò riflette la situazione di carico effettiva quando il calcestruzzo viene caricato solo per un breve periodo. Questo valore è particolarmente rilevante per la verifica di carichi di breve durata.

α_e,I,st = 2 ⋅ 10⁵ MN/m²/30.000 MN/m² = 6,67

Rapporto modulare efficace per stato fessurato α_e,II
Nello stato fessurato, il calcestruzzo nella zona tesa non è considerato portante. Il rapporto α_e,II ne tiene conto includendo solo il modulo di elasticità efficace del calcestruzzo's E_c,eff. Questo valore mostra che la rigidezza dell'acciaio è maggiore nello stato fessurato rispetto al calcestruzzo, sottolineando l'importanza dell'armatura in questi casi.

α_e,II = 2 ⋅ 10⁵ MN/m²/10.001,2 MN/m² = 20,00

Parametri geometrici non fessurati

La distanza del baricentro della sezione trasversale ideale nello stato non fessurato sotto carico di lunga durata, z_I , descrive la posizione del baricentro, tenendo conto dell'area del calcestruzzo e dell'armatura. L'effetto dell'armatura è ridimensionato da un coefficiente di conversione α_e,l, che rappresenta il rapporto tra il modulo di elasticità dell'acciaio e il modulo di elasticità efficace del calcestruzzo. Ciò è particolarmente importante perché il carico a lungo termine, come la viscosità, indebolisce il calcestruzzo. Il baricentro influenza il calcolo dei momenti e degli spostamenti generalizzati nella sezione trasversale ed è quindi un parametro centrale per l'analisi strutturale.

L' area efficace della sezione nello stato non fessurato con carico di lunga durata, A_I , rappresenta i carichi portanti dell'area efficace. Oltre all'area del calcestruzzo, viene presa in considerazione anche l'area di armatura, che è integrata dal coefficiente α_e,l. In questo modo, la rigidezza della sezione trasversale è rappresentata in modo più realistico. Questo valore è decisivo per la valutazione della capacità portante e per il calcolo della deformazione del componente strutturale.

A_I = 1.000 mm ⋅ 200 mm + 20 ⋅ (4,45 cm² + 0 cm²) = 2.089,05 cm²

Il momento di inerzia efficace del baricentro ideale nello stato non fessurato sotto carico di lunga durata,_II , descrive la resistenza alla flessione della sezione trasversale. Tiene conto sia della superficie del calcestruzzo che dell'armatura, sebbene quest'ultima generi momenti aggiuntivi a causa della sua posizione rispetto al baricentro. Questo momento di inerzia è un fattore chiave nell'analisi degli spostamenti generalizzati e mostra quanti momenti flettenti può sopportare la sezione trasversale.

L' eccentricità del baricentro ideale della sezione trasversale nello stato non fessurato, e_I , indica la deviazione del baricentro dal centro geometrico della sezione trasversale. Questa eccentricità è importante poiché influenza i momenti sviluppati nella sezione trasversale, che influenzano direttamente gli spostamenti generalizzati.

e_I = 103 mm - 200 mm/2 = 3 mm

La distanza del baricentro della sezione trasversale ideale nello stato non fessurato sotto carico di breve durata, z_I,st descrive la posizione del baricentro sotto carichi che non considerano gli effetti di viscosità o ritiro. Pertanto, il coefficiente di conversione α_e,I,st utilizzato nel calcolo a breve termine è inferiore a quello per i carichi a lungo termine. Questa distanza del baricentro è decisiva per la distribuzione dei carichi e la determinazione dei momenti nei carichi a breve termine.

L' area della sezione efficace nello stato non fessurato con carico a breve termine, A_I,st , è simile all'area A_I ma modificata dal coefficiente di conversione α_e,I,st, che non tiene conto degli effetti a lungo termine. Ciò si tradurrà in un'area più piccola e avrà un impatto sul calcolo della resistenza per carichi a breve termine.

A_I,st = 1.000 mm ⋅ 200 mm + 6,67 ⋅ (4,45 cm² + 0 cm²) = 2.029,69 cm²

Il momento di inerzia efficace del baricentro ideale nello stato non fessurato sotto carico di breve durata, I_I,st, rappresenta la resistenza della sezione trasversale alla flessione senza l'influenza di effetti a lungo termine. Tiene conto sia del calcestruzzo che dell'area di armatura e delle loro distanze dal baricentro, che sono cruciali per il calcolo della deformazione sotto carichi a breve termine.

Parametri geometrici incrinati

La distanza del baricentro della sezione trasversale ideale nello stato fessurato, z_II , tiene conto della resistenza modificata della sezione trasversale poiché la zona di trazione del calcestruzzo non supporta più alcun carico dopo la formazione di fessure. La posizione del baricentro sarà ricalcolata tenendo conto solo della zona di compressione del calcestruzzo' e dell'armatura. Questo parametro è fondamentale per l'analisi della sezione trasversale dopo la fessura e influenza la resistenza e la deformazione.

L' area della sezione trasversale efficace nello stato fessurato, A_II , rappresenta l'area rimanente dopo la formazione di fessure. Qui, vengono considerate solo la zona di compressione del calcestruzzo e l'area di armatura, il che riduce notevolmente la rigidezza della sezione trasversale. Questo valore è cruciale per la verifica allo stato limite ultimo in caso di sezioni trasversali fessurate.

A_II = 1.000 mm ⋅ 46,8 mm + 20 ⋅ (4,45 cm² + 0) = 557,41 cm²

Il momento di inerzia efficace del baricentro ideale nello stato fessurato, I_II , descrive la resistenza alla flessione dopo la fessurazione. Poiché la zona di trazione non è più portante, il momento di inerzia si riduce notevolmente. Questo valore è un fattore essenziale per il calcolo della deformazione e per la valutazione della resistenza delle sezioni fessurate.

L' eccentricità del baricentro della sezione trasversale ideale's nello stato fessurato, e_II , descrive lo spostamento del baricentro dovuto alla formazione di fessure. Questo spostamento influenza i momenti risultanti e la deformazione della sezione trasversale, ed è quindi un parametro importante per l'analisi strutturale.

e_II = 46,8 mm - 200 mm/2 = -53,2 mm

ritiro

La forza assiale dovuta al ritiro, N_sh , si verifica perché l'armatura non sopporta la deformazione del calcestruzzo causata dal ritiro e quindi assorbe le forze. Queste forze risultano dall'interazione tra la forza di trazione del calcestruzzo e la risposta dell'armatura. Il valore calcolato mostra quanto pesantemente l'armatura è caricata dal ritiro. A questo punto, viene utilizzata la deformazione da ritiro ε_sh = -0.5‰, che è definita dall'utente indirettamente.

N_sh = -2 ⋅ 10⁵ MN/m² ⋅ ( -0.000.5 ) ⋅ ( 4.45 cm² + 0.00 ) = 44.532 kN

L' eccentricità della forza di ritiro rispetto al baricentro della sezione trasversale ideale nello stato non fessurato, e_sh,I , descrive la posizione della forza di ritiro risultante rispetto al centro di gravità della sezione trasversale. Un'eccentricità maggiore porta a momenti più elevati e deformazioni maggiori.

e_sh,I = (4,45 cm² ⋅ 170 mm + 0)/(4,45 cm² + 0) - 103 mm = 67 mm

Il momento di ritiro per lo stato non fessurato M_sh,I risulta dalla forza di ritiro N_sh e dall'eccentricità e_sh,I. Mostra come la forza di ritiro crea un momento attraverso il suo effetto sulla sezione trasversale. Questo momento ha un'influenza significativa sugli spostamenti generalizzati e sulle tensioni nella sezione trasversale e deve essere considerato nella verifica.

M_sh,I = 44,532 kN ⋅ 67 mm = 2,98 kNm

Il coefficiente di curvatura per lo stato non fessurato k_sh,I indica come agisce il momento di ritiro in relazione alla forza assiale e all'eccentricità. Mostra come la distribuzione della forza di ritiro e la posizione del baricentro influenzano le deformazioni del componente strutturale. Questo valore è fondamentale per descrivere completamente le deformazioni della sezione trasversale dovute al ritiro.

k_sh,I = ( 2.98 kNm + 18.5 kNm - 0 )/( 18.50 kNm – 0 ) = 1.161

L' eccentricità della forza di ritiro rispetto al baricentro della sezione trasversale ideale nello stato fessurato, e_sh,II , descrive la posizione della forza di ritiro risultante in relazione al centro di gravità della sezione trasversale nella fessurata stato. I momenti dell'area dell'armatura, A_{s,def, +z,(inferiore)} e A_{s,def, -z,(superiore)}, sono determinati rispetto alla loro posizione, d_{ef, +z,(inferiore)} e d_{ef, -z,(superiore)} e lo divide per l'area totale dell'armatura. La distanza del baricentro della sezione trasversale fessurata, z_II, è sottratta dal risultato. Questa eccentricità influenza il momento di ritiro, perché un'eccentricità maggiore porta a un momento maggiore.

e_sh,II = (4,45 cm² ⋅ 170 mm + 0)/(4,45 cm² + 0) – 46,8 mm = 123,2 mm

Il momento flettente per la forza assiale N_sh per lo stato fessurato M_sh,II si ottiene moltiplicando la forza di ritiro N_sh per l'eccentricità precedentemente calcolata e_sh,II. Questo momento descrive la tensione di flessione aggiuntiva che agisce sulla sezione trasversale a causa della forza di ritiro. Questo valore è particolarmente rilevante nello stato fessurato, dove la zona di trazione del calcestruzzo non supporta più alcun carico.

M_sh,II = 44,532 kN ⋅ 123,2 mm = 5,48 kNm

Il coefficiente di curvatura per lo stato fessurato, k_sh,II , indica quanto fortemente la deformazione della sezione trasversale è influenzata dal momento di ritiro e dalle altre forze agenti. Vengono presi in considerazione il momento di ritiro M_sh,II, il momento flettente esistente My_,Ed,def, nonché la forza assiale N_Ed e la sua eccentricità e_II. Il calcolo pone il momento risultante in proporzione al momento senza ritiro e fornisce quindi una misura per l'influenza della forza di ritiro.

k_sh,II = ( 5.48 kNm + 18.50 kNm - 0 )/( 18.50 kNm - 0 ) = 1.296

Spostamento generalizzato della sezione

Una deformazione della sezione trasversale è la curvatura di un componente strutturale causata da azioni esterne, tenendo conto del suo materiale e dei parametri di stato.

Il calcolo della deformazione della sezione trasversale nello stato non fessurato, κ_I , descrive la curvatura della sezione trasversale causata dal momento di ritiro e le proprietà elastiche del materiale. Il momento di ritiro My_,Ed,def è preso in considerazione così come la forza assiale_NEd e la sua eccentricità e_I. Questi valori sono moltiplicati per il coefficiente k_sh,I, che descrive l'influenza del momento di ritiro nello stato non fessurato. Il denominatore include il modulo di elasticità efficace del calcestruzzo's, E_c,eff, e il momento di inerzia della sezione trasversale non fessurata, I_I, che determinano la rigidezza della sezione trasversale's.

κ_I = (1,161 ⋅ (18,50 kNm - 0))/(10.001,2 MN/m² ⋅ 70.844,30 cm⁴)
= 3 mrad/m

Il calcolo della deformazione della sezione nello stato fessurato, κ_II , mostra la curvatura della sezione dopo la formazione di fessure, tenendo conto del momento di ritiro e della resistenza ridotta della sezione fessurata. Qui, il momento di ritiro My_,Ed,def, la forza assiale_NEd e la sua eccentricità e_II sono moltiplicati per il coefficiente k_sh,II, che descrive l'influenza del momento di ritiro nello stato fessurato. Al denominatore, il modulo di elasticità efficace del calcestruzzo's, E_c,eff, e il momento di inerzia ridotto della sezione trasversale fessurata, I_II, sono persi, che riflettono la sezione trasversale's minore rigidezza. La deformazione della sezione trasversale nello stato fessurato è significativamente maggiore rispetto allo stato non fessurato perché la rigidezza della sezione trasversale fessurata è ridotta.

κ_II = (1,296 ⋅ (18,50 kNm - 0))/(10.001,2 MN/m² ⋅ 16.933,50 cm⁴) = 14,2 mrad/m

Stato finale

Lo stato finale descrive le tensioni massime che possono verificarsi nella sezione trasversale non fessurata sotto carichi sia a lungo che a breve termine al fine di garantire la capacità portante e l'esercizio del componente strutturale.

La tensione massima nello stato non fessurato sotto carico di lunga durata, σ_max, Descrive la tensione massima che può verificarsi nella sezione trasversale non fessurata come risultato del carico di lunga durata. È composto da due parti:

• il contributo delle forze assiali_NEd e_Nsh
• il contributo dei momenti flettenti My_,Ed,def, M_sh,I e il momento derivante dall'eccentricità (z_I - h/2) della forza assiale_NEd.

La seconda parte è amplificata dal momento di inerzia I_I e dalla distanza (h - z_I ).

La tensione massima nello stato non fessurato sotto carico di breve durata, σ_max,st indica la tensione maggiore nella sezione trasversale sotto carichi di breve durata. A differenza del carico di lunga durata, qui vengono considerate solo la forza assiale_NEd e My_,Ed,def poiché non ci sono forze interne da ritiro.

La tensione massima nello stato non fessurato, σ_max , è il maggiore dei due valori di tensione dovuti al carico a lungo ea breve termine. Garantisce che venga preso in considerazione il carico più alto possibile della sezione trasversale.

σ_max = max ( 3.155 MN/m²; 2.689 MN/m² )
= 3.155 MN/m²

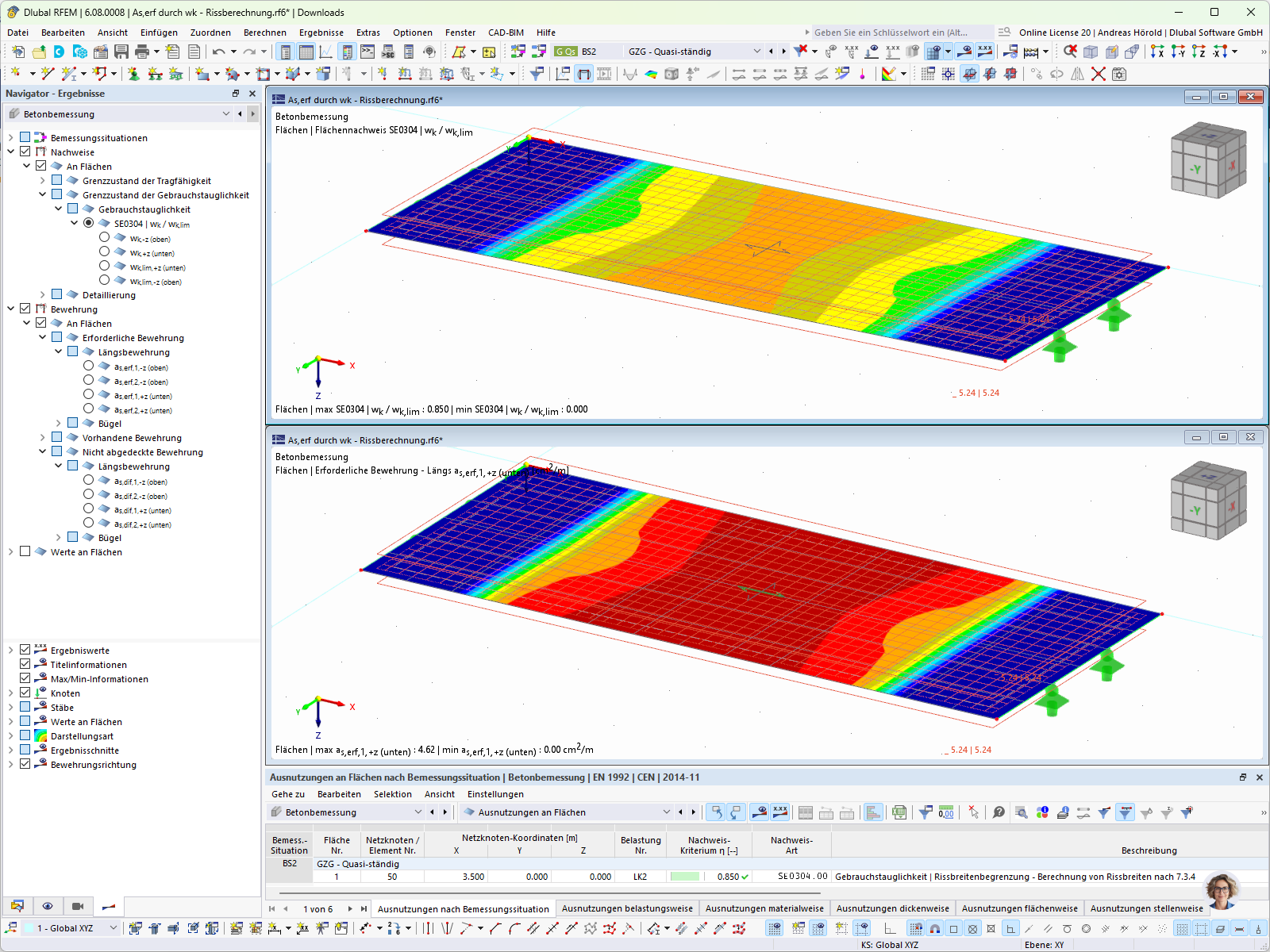
Il coefficiente di distribuzione (parametro di danneggiamento) ζ_d descrive la transizione tra il comportamento della sezione trasversale nello stato non fessurato e quello fessurato. È calcolato dal rapporto tra la resistenza a trazione caratteristica del calcestruzzo, f_ctm, e la tensione massima, σ_max. In questo caso, la non linearità è presa in considerazione dalla relazione esponenziale.

ζ_d = 1 – 0,5 ⋅ (2.200 MN/m²/3.155 MN/m²)²
= 0,757 ≤ 1
con:
β = 1.0 (carico di breve durata)
β = 0.5 (carico di lunga durata o molti cicli di carico ripetitivo)
Se il coefficiente di distribuzione ζ_d = 1, il componente strutturale è completamente nello stato fessurato. D'altra parte, se ζ_d è uguale a 0, il calcestruzzo è completamente non fessurato.

Per il calcolo del coefficiente di distribuzione ζ_d, è importante quale opzione è selezionata per il rilevamento dello stato di fessurazione. Quando si seleziona l'opzione "Stato di fessurazione calcolato dal carico associato", lo stato di fessurazione (coefficiente di distribuzione ζ_d ) viene calcolato esclusivamente dal carico corrente (combinazione di carico), come in questo esempio. Le altre opzioni sono descritte nel manuale.

La curvatura della sezione, κ_f , è calcolata per interpolazione tra lo stato fessurato (κ_II ) e non fessurato (κ_I ), ponderato dal coefficiente di distribuzione, ζ_d. Ciò consente una descrizione realistica del comportamento della curvatura nello stato di transizione.

κ_f = 0,757 ⋅ 14,2 mrad/m + (1 – 0,757) ⋅ 3 mrad/m
= 11,5 mrad/m
L' area della sezione trasversale ideale, A_f , descrive la transizione tra l'area della sezione trasversale non fessurata, A_I, e l'area della sezione trasversale fessurata, A_II. Anche in questo caso, la ponderazione viene eseguita dal coefficiente di distribuzione, ζ_d.


Il momento di inerzia ideale I_y,f descrive il momento della sezione trasversale tenendo conto del coefficiente di distribuzione ζ_d, nonché dei momenti di inerzia nello stato non fessurato I_I e nello stato fessurato I_II. Fattori aggiuntivi come k_sh,II e k_sh, considero gli effetti del ritiro nel rispettivo stato.


L' eccentricità del baricentro,_ef , descrive la posizione del baricentro risultante della sezione trasversale, in base alla transizione tra lo stato non fessurato e quello fessurato. Tiene conto del coefficiente di distribuzione, ζ_d, nonché dei rispettivi moduli di elasticità, E_c,eff, e dei momenti di inerzia, I_I e I_II.


Il momento di inerzia ideale rispetto al centro geometrico della sezione trasversale I_y,0,f , considera oltre al momento di inerzia ideale I_y,f, e l'area della sezione trasversale ideale A_f, anche lo spostamento del baricentro dovuto all'eccentricità e_f. Questo spostamento è preso in considerazione dalla componente di Steiner di A_f.

I_y,0,f = 16.145,50 cm⁴ + 678,30 cm² ⋅ (-49,2 mm)²
= 32.538,80 cm⁴

Rigidezza finale

Le rigidezze finali di un componente strutturale descrivono la sua resistenza a deformazioni e rotazioni sotto diversi tipi di carichi. Il programma considera le rigidezze assiali e flessionali, nonché le rigidezze torsionali e di taglio. Questi valori sono utilizzati come base per l'analisi del comportamento strutturale e dello stato di esercizio di un componente strutturale.
La rigidezza tangente della membrana EA_f descrive la rigidezza assiale della sezione trasversale tenendo conto del modulo di elasticità efficace del calcestruzzo 's E_c,eff e dell'area ideale della sezione trasversale A_f.

EA_f = 10.001,2 MN/m² ⋅ 678,30 cm²
= 678.387 kN
La rigidezza flessionale tangente, EI_y,0,f , descrive la resistenza della sezione trasversale' alla flessione intorno al baricentro ideale. È determinato dal modulo di elasticità efficace del calcestruzzo E_c,eff e dal momento ideale dell'area I_y,0,f.

EI_y,0,f = 10.001,2 MN/m² ⋅ 32.538,80 cm⁴
= 3.254,28 kNm²
La resistenza a flessione tangente, EI_z,0,f , descrive la resistenza della sezione trasversale's alla flessione intorno all'asse locale z. È definito dal modulo di elasticità efficace del calcestruzzo 's E_c,eff e dal secondo momento dell'area attorno all'asse z I_z.

EI_z,0,f = 10.001,2 MN/m² ⋅ 1.666.670 cm⁴
= 166.687 kNm²

Il coefficiente r descrive la riduzione della rigidezza a taglio basata sul rapporto dei momenti di inerzia ideali I_f e I_I.

r = 16.145,50 cm⁴/70.844,30 cm⁴
= 0,228
La rigidezza a taglio sull'asse y GA_y,f tiene conto del modulo di taglio efficace del calcestruzzo's G_c,eff, dell'area della sezione trasversale A_c,y e del coefficiente di riduzione r.

GA_y,f = 4.167,18 MN/m² ⋅ 1.666,67 cm² ⋅ 0,228
= 158.284 kN
La rigidezza a taglio sull'asse z, GA_z,f , è calcolata allo stesso modo dell'asse y.

GA_z,f = 4.167,18 MN/m² ⋅ 1.666,67 cm² ⋅ 0,228
= 158.284 kN
La rigidezza torsionale GI_T,f corrisponde nel caso considerato alla rigidezza torsionale nello stato non fessurato GI_T,I.

GI_T,f = 7.770 kNm²
L' elemento di rigidezza eccentrica ES_y descrive il carico aggiuntivo della sezione trasversale causato dall'eccentricità e_f. Viene calcolato utilizzando la rigidezza assiale EA_f e l'eccentricità e_f.

ES_y = 678,387 kN ⋅ ( -49,2 mm )
= -33.350,20 kNm

Inflessione e vincoli esterni di progetto

Per garantire lo stato di esercizio, la deformazione effettiva viene confrontata con i valori limite ammissibili. L'inflessione totale intorno alla controfreccia viene corretta e verificata rispetto ai valori limite specificati.
Quando si calcola l'inflessione, la combinazione di carico principale è considerata senza effetti dipendenti dal tempo come viscosità e ritiro (a breve termine), mentre le combinazioni di carico corrispondenti sono sempre calcolate con proprietà dipendenti dal tempo (a lungo termine). Se è disponibile più di un carico corrispondente, viene presa come base l'inflessione del carico con il valore più alto.
L' inflessione limite in direzione z uz_,lim è calcolata con la lunghezza di riferimento in direzione z L_z,ref, e il criterio di inflessione limite L_z,ref/u_z,lim.

u_z,lim = 4,210 m/250 = 16,8 mm
L' inflessione nella direzione z,_uz , risulta dalla differenza dell'inflessione totale uz_,tot, e della controfreccia nella posizione x,_uz,c.

u_z = 19,4 mm - 0 = 19,4 mm

progettazione

η = max (19,4 mm/16,8 mm; 0,0 mm/16,8 mm) = 1,155 Poiché η = 1.155 > 1, l'inflessione ammissibile è stata superata!

Conclusione

Il calcolo degli spostamenti generalizzati secondo i metodi di approssimazione definiti nelle norme, come l'analisi degli spostamenti generalizzati secondo la sezione 7.4.3 della EN 1992-1-1, viene eseguito utilizzando rigidezze efficaci che sono calcolate agli elementi finiti secondo lo stato limite (fessurato o non fessurato). Queste rigidezze efficaci costituiscono la base per il successivo calcolo della deformazione del componente strutturale utilizzando un'ulteriore analisi FEM.

La sezione trasversale di cemento armato è considerata per la determinazione delle rigidezze efficaci, per cui la sezione trasversale di cemento armato è classificata in "fessurata" o "non fessurata" per lo stato limite di esercizio sulla base delle forze interne determinate. L'effetto del calcestruzzo tra le fessure è considerato da un coefficiente di distribuzione, ad esempio secondo l'equazione 7.19 (EN 1992-1-1). Si presume che il comportamento del materiale del calcestruzzo sia lineare-elastico fino alla resistenza a trazione del calcestruzzo, che è sufficientemente precisa per la condizione di esercizio.

Gli effetti a lungo termine della viscosità e del ritiro sono presi in considerazione quando si determinano le rigidezze efficaci a livello della sezione trasversale del componente strutturale al fine di garantire una rappresentazione realistica delle deformazioni sotto carichi a lungo termine.