Bezpośrednia analiza odkształcenia belki żelbetowej z uwzględnieniem pełzania i skurczu

W niniejszym artykule technicznym przedstawiono bezpośrednią analizę deformacji belki żelbetowej, dodatkowo z uwzględnieniem długotrwałych efektów pełzania i skurczu. Na przykładzie pokazano, w jaki sposób efekty te wpływają na odkształcenie elementu konstrukcyjnego i są uwzględniane w obliczeniach. Wyjaśniono w niej, które dane są niezbędne w programie RFEM 6, aby poprawnie uwzględnić wszystkie istotne współczynniki oraz w jaki sposób współczynnik rozkładu wpływa na sztywność elementu konstrukcyjnego.

Dane wejściowe

Geometria, zbrojenie i obciążenie są opisane przez następujące parametry:

system

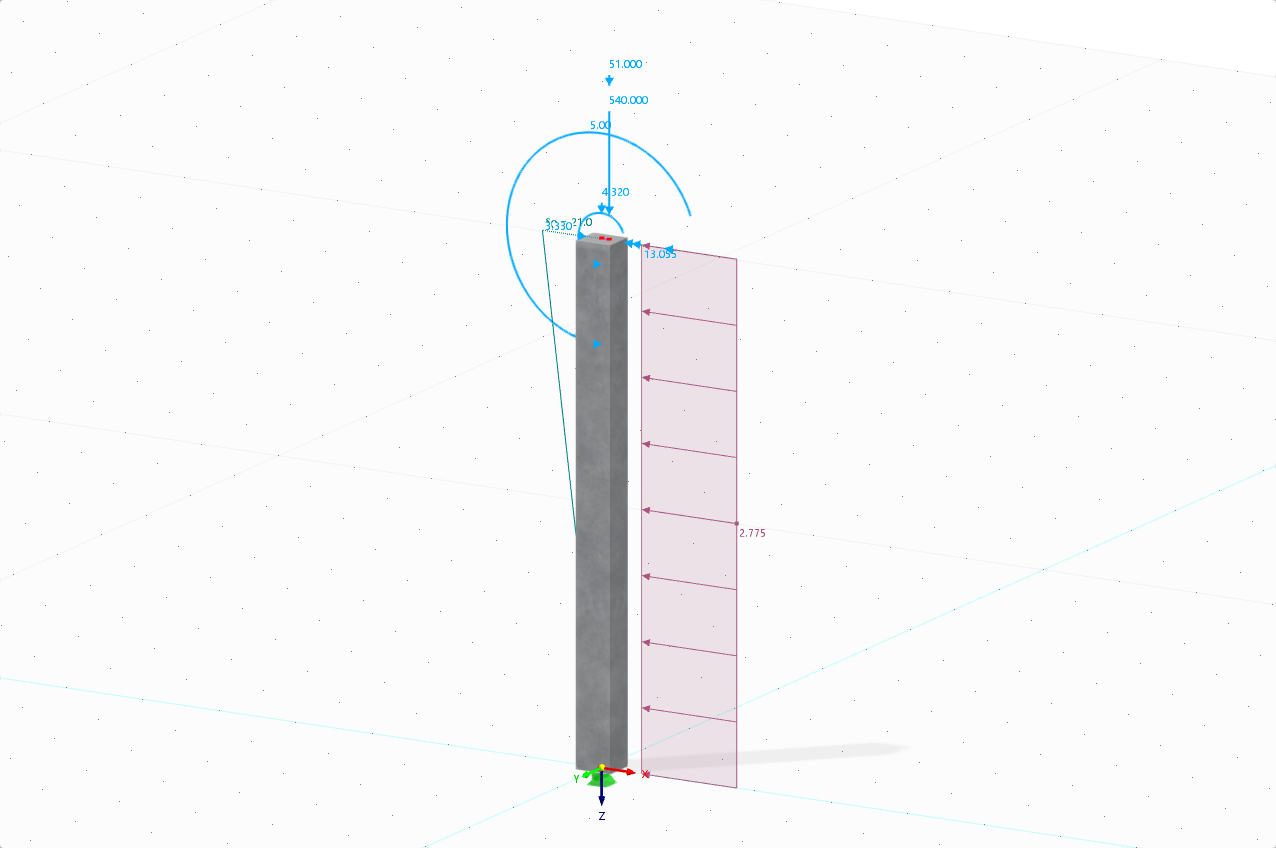
• Typ belki: Prosta belka
• Długość przęsła: l = 4,210 m²

Przekrój

• Grubość płyty: h = 7,8 in
• Szerokość płyty b = 100 cm
• Materiał: Beton C20/25 z E_cm = 30.000 MN/m² i B 500A
• Zbrojenie: A_{s,-z,(bottom)} = 4,45 cm² gdzie 7 ∅ 9 i d₁ = 30 mm
• Wysokość użyteczna dolnego zbrojenia: d_{def, + z (dół)} = 17 cm

Obciążenia stałe

• Ciężar własny: g_s = 0,20 m ⋅ 1 m ⋅ 25 kN/m³ = 5,00 kN/m
• Tynk i posadzki: g_bp = 1,50 kN/m
• Suma: g_k,total = 6,5 kN/m

Obciążenia zmienne

• Obciążenie zmienne (Office): q_b = 2,00 kN/m przy ψ₂ = 0,3
• Kompensacja przegrody: q_t = 1,25 kN/m przy ψ₂ = 1,0

Obciążenie quasi-stałe

• 6,5 kN/m + 0,3 ⋅ 2,00 kN/m + 1,0 ⋅ 1,25 kN/m = 8,35 kN/m

Obliczeniowy moment zginający do obliczania ugięć

• My_,Ed,def = 8,35 kN/m ⋅ (4,21 m)²/8 = 18,50 kNm

Początkowe wartości odkształceń

• Średni moduł sprężystości betonu: E_cm = 30 000 MN/m²

• Stopień zbrojenia podłużnego: ρ = A_s/A_c = 4,45 cm²/(20 cm ⋅ 100 cm) = 0,223%

• Odkształcenie skurczowe: ε_sh = -0,5 ‰
• Współczynnik pełzania: φ = 2

Aby określić współczynnik pełzania za pomocą ustawień zdefiniowanych przez użytkownika, w ustawieniach przekroju należy aktywować opcję "Zaawansowane właściwości betonu zależne od czasu".

W dostępnej teraz zakładce należy najpierw wybrać opcje „Pełzanie” i „Skurcz”, aby wyświetlić i edytować „Podstawowe wartości właściwości zależnych od czasu”. Współczynnik pełzania φ został określony poprzez wprowadzenie φ₀, ϵ_cd,0 i ϵ_ca(∞).

Pełzanie

Efekty pełzania są określane przez redukcję modułu sprężystości betonu's E_c.

Efektywny moduł sprężystości E_{c, eff} uwzględnia długotrwałe wpływy betonu, zwłaszcza pełzanie. Pełzanie opisuje długotrwałe odkształcenie betonu pod stałym obciążeniem. Współczynnik pełzania φ zmniejsza moduł sprężystości E_cm (średni moduł sprężystości betonu), dzięki czemu rzeczywista sztywność betonu jest odwzorowana w długim okresie czasu. Wartość ta jest wykorzystywana w dalszych obliczeniach, np. dla momentu bezwładności lub stosunku sztywności.

E_c,eff = 30 000 MN/m²/( 1 + 2 ) = 10 001,2 MN/m²

Efektywny moduł ścinania betonu G_c,eff
Efektywny moduł ścinania opisuje odporność betonu na odkształcenia od ścinania i jest określany jako stosunek odkształcenia poprzecznego do odkształcenia podłużnego (współczynnik Poissona v betonu). Wartość ta jest szczególnie istotna przy obliczaniu odkształceń przekroju i przy sprawdzaniu ścinania.

G_{c, eff} = 10 001,2 MN/m²/( 2 ⋅ ( 1 + 0,2 ) ) = 4 167,180 MN/m²

Efektywny stosunek modułów sprężystości dla stanu niezarysowanego (obciążenie długotrwałe) α_e,l
Stosunek α_{e, l} wskazuje, o ile sztywniejsza jest stal w porównaniu z betonem pod obciążeniem długotrwałym. E_s jest modułem sprężystości stali, E_{c, l} jest efektywnym modułem sprężystości betonu w stanie niezarysowanym (identycznym jak E_{c, eff} ). Ponieważ beton ma niższą sztywność ze względu na długotrwałe efekty, takie jak pełzanie, wartość α_{e, l} w tym stanie jest wyższa. Stosunek ten jest wykorzystywany w obliczeniach środka ciężkości i właściwości przekroju efektywnego.

α_{e, l} = 2 ⋅ 10⁵ MN/m²/10 0001,2 MN/m² = 20

Efektywny stosunek modułów sprężystości dla stanu niezarysowanego (obciążenie krótkotrwałe) α_e,I,st
Stosunek α_e,I,st opisuje stosunek sztywności stali do betonu pod obciążeniem krótkotrwałym. W przeciwieństwie do α_{e, l,} zastosowano tutaj średni moduł sprężystości E_cm bez uwzględnienia efektów pełzania. Odzwierciedla to rzeczywistą sytuację obciążenia, gdy beton jest obciążony tylko przez krótki czas. Wartość ta jest szczególnie istotna przy obliczaniu obciążeń krótkotrwałych.

α_e,I,st = 2 ⋅ 10⁵ MN/m²/30 000 MN/m² = 6,67

Efektywny stosunek modułów sprężystości dla stanu zarysowanego α_e,II
W stanie zarysowanym beton w strefie rozciąganej nie jest uznawany za nośny. Stopień wykorzystania α_e,II uwzględnia tylko efektywny moduł sprężystości betonu' E_c,eff. Wartość ta wskazuje, że sztywność stali jest wyższa w stanie zarysowanym w porównaniu z sztywnością betonu, co podkreśla znaczenie zbrojenia w takich przypadkach.

α_e,II = 2 ⋅ 10⁵ MN/m²/10 000,2 MN/m² = 20,00

Parametry geometryczne w stanie niezarysowanym

Odległość środka ciężkości idealnego przekroju w stanie niezarysowanym i obciążeniu długotrwałym, z_I , opisuje położenie środka ciężkości z uwzględnieniem powierzchni betonu i zbrojenia. Efekt zbrojenia jest skalowany przy użyciu współczynnika konwersji α_{e, l}, który stanowi stosunek modułu sprężystości stali do efektywnego modułu sprężystości betonu. Jest to szczególnie ważne, ponieważ długotrwałe obciążenia, takie jak pełzanie, osłabiają beton. Środek ciężkości wpływa na obliczanie momentów i odkształceń w przekroju, a tym samym jest głównym parametrem w analizie statyczno-wytrzymałościowej.

Efektywne pole przekroju w stanie niezarysowanym przy obciążeniu długotrwałym, A_I , reprezentuje efektywne pole przenoszące obciążenia. Oprócz powierzchni betonu uwzględniane jest również pole przekroju zbrojenia, które jest uzupełniane o współczynnik α_{e, l}. W ten sposób sztywność przekroju jest przedstawiana bardziej realistycznie. Wartość ta jest decydująca dla oceny nośności oraz dla obliczeń odkształcenia elementu konstrukcyjnego.

A_I = 1000 mm ⋅ 200 mm + 20 ⋅ (4,45 cm² + 0 cm²) = 2 089,05 cm²

Efektywny moment bezwładności idealnego środka ciężkości w stanie niezarysowanym pod obciążeniem długotrwałym_II opisuje wytrzymałość przekroju na zginanie. Uwzględnia się tu zarówno powierzchnię betonu, jak i zbrojenie, chociaż to drugie generuje dodatkowe momenty ze względu na swoje położenie względem środka ciężkości. Ten moment bezwładności jest kluczowym czynnikiem w analizie odkształceń i pokazuje, ile momentów zginających może wytrzymać przekrój.

Mimośród idealnego środka ciężkości przekroju w stanie niezarysowanym, e_I , wskazuje odchylenie środka ciężkości od geometrycznego środka przekroju. Mimośród ten jest istotny, ponieważ wpływa na momenty powstające w przekroju, które bezpośrednio wpływają na odkształcenia.

e_I = 103 mm - 200 mm/2 = 3 mm

Odległość środka ciężkości idealnego przekroju w stanie niezarysowanym i przy krótkotrwałym obciążeniu, z_,st opisuje położenie środka ciężkości pod obciążeniami, które nie uwzględniają efektów pełzania lub skurczu. Z tego względu współczynnik konwersji α_e,I,st stosowany w obliczeniach krótkotrwałych jest mniejszy niż w przypadku obciążeń długotrwałych. Ta odległość środka ciężkości ma decydujące znaczenie dla rozkładu obciążeń i określania momentów w obciążeniach krótkotrwałych.

Efektywne pole przekroju w stanie niezarysowanym przy krótkotrwałym obciążeniu A_I,st , jest podobne do pola przekroju A_I, ale skorygowane o współczynnik konwersji α_e,I,st, który nie uwzględnia efektów długotrwałych. Spowoduje to zmniejszenie powierzchni i będzie miało wpływ na obliczenia nośności dla obciążeń krótkotrwałych.

A_I,st = 1000 mm ⋅ 200 mm + 6,67 ⋅ (4,45 cm² + 0 cm²) = 2 029,69 cm²

Efektywny moment bezwładności idealnego środka ciężkości w stanie niezarysowanym pod obciążeniem krótkotrwałym, I_,st, przedstawia wytrzymałość przekroju na zginanie bez wpływu efektów długotrwałych. Uwzględnia się w niej zarówno powierzchnię betonu, jak i zbrojenia oraz ich odległości od środka ciężkości, które mają kluczowe znaczenie dla obliczania odkształceń pod wpływem obciążeń krótkotrwałych.

Parametry geometryczne zarysowania

Odległość środka ciężkości idealnego przekroju w stanie zarysowanym,_zII , uwzględnia zmodyfikowaną nośność przekroju, ponieważ po zarysowaniu strefa rozciągania betonu nie przenosi już żadnych obciążeń. Położenie środka ciężkości zostanie obliczone ponownie z uwzględnieniem tylko strefy ściskanej i zbrojenia betonu. Parametr ten ma kluczowe znaczenie dla analizy przekroju po zarysowaniu i wpływa na nośność i odkształcenie.

Efektywne pole przekroju w stanie zarysowanym, A_II , stanowi powierzchnię pozostałą po zarysowaniu. Uwzględniana jest tu tylko strefa ściskania betonu i powierzchnia zbrojenia, co znacznie zmniejsza sztywność przekroju. Wartość ta ma decydujące znaczenie dla obliczeń stanu granicznego nośności w przypadku przekrojów zarysowanych.

A_II = 1,000 mm ⋅ 46,8 mm + 20 ⋅ (4,45 cm² + 0) = 557,41 cm²

Efektywny moment bezwładności idealnego środka ciężkości w stanie zarysowanym, I_II , opisuje nośność na zginanie po zarysowaniu. Ponieważ strefa rozciągana nie jest już nośna, moment bezwładności jest znacznie zredukowany. Wartość ta jest istotnym współczynnikiem do obliczania odkształcenia i do oceny nośności przekrojów zarysowanych.

Mimośród środka ciężkości przekroju idealnego's w stanie zarysowanym,_eII , opisuje przesunięcie środka ciężkości w wyniku zarysowania. Przemieszczenie to ma wpływ na momenty wypadkowe i odkształcenie przekroju, dlatego jest ważnym parametrem w analizie statyczno-wytrzymałościowej.

e_II = 46,8 mm - 200 mm/2 = -53,2 mm

Skurcz

Siła osiowa spowodowana skurczem,_Nsh , powstaje, ponieważ zbrojenie nie przenosi odkształceń betonu wywołanych skurczem, a tym samym przejmuje siły. Siły te wynikają z interakcji między siłą rozciągającą beton a odpowiedzią zbrojenia. Obliczona wartość pokazuje, jak bardzo zbrojenie jest obciążone skurczem. W tym momencie stosuje się odkształcenie skurczowe ε_sh = -0.5 ‰, które jest pośrednio zdefiniowane przez użytkownika.

N_sh = -2 ⋅ 10⁵ MN/m² ⋅ ( -0.000.5 ) ⋅ ( 4.45 cm² + 0,00 ) = 44,532 kN

Mimośród siły skurczowej w kierunku środka ciężkości przekroju idealnego w stanie niezarysowanym, e_{sh, I} , opisuje położenie wynikowej siły skurczowej względem środka ciężkości przekroju. Większy mimośród prowadzi do większych momentów i odkształceń.

e_sh,I = (4,45 cm² ⋅ 170 mm + 0)/(4,45 cm² + 0) - 103 mm = 67 mm

Moment skurczowy dla stanu niezarysowanego M_sh,I wynika z siły skurczu N_sh oraz mimośrodu e_sh,I. Pokazuje, w jaki sposób siła skurczowa tworzy moment poprzez swój wpływ na przekrój. Moment ten ma znaczny wpływ na odkształcenia i naprężenia w przekroju i musi zostać uwzględniony w obliczeniach.

M_sh,I = 44,532 kN ⋅ 67 mm = 2,98 kNm

Współczynnik krzywizny dla stanu niezarysowanego k_sh,I wskazuje, w jaki sposób działa moment skurczowy w odniesieniu do siły osiowej i mimośrodu. Pokazuje on, w jaki sposób rozkład siły skurczu oraz położenie środka ciężkości wpływają na odkształcenia elementu konstrukcyjnego. Wartość ta jest kluczowa dla pełnego opisania odkształceń przekroju spowodowanych skurczem.

k_sh,I = ( 2,98 kNm + 18,5 kNm - 0 )/( 18,50 kNm – 0 ) = 1,161

Mimośród siły skurczowej w kierunku środka ciężkości idealnego przekroju w stanie zarysowanym, e_sh,II , opisuje położenie wypadkowej siły skurczowej względem środka ciężkości przekroju w zarysowanym stan. Momenty powierzchniowe zbrojenia, A_{s,def, +z,(bottom)} i A_{s,def, -z,(top)}, są określane w odniesieniu do ich położenia d_{ef, +z,(bottom)} i d_{ef, -z,(top)} i dzieli przez całkowite pole przekroju zbrojenia. Od wyniku odejmuje się odległość środka ciężkości zarysowanego przekroju z_II. Ten mimośród wpływa na moment skurczowy, ponieważ większy mimośród prowadzi do większego momentu.

e_sh,II = (4,45 cm² ⋅ 170 mm + 0)/(4,45 cm² + 0) – 46,8 mm = 123,2 mm

Moment zginający i siłę osiową N_sh dla stanu zarysowanego M_sh,II uzyskuje się poprzez pomnożenie siły skurczu N_sh przez wcześniej obliczony mimośród e_sh,II. Moment ten opisuje dodatkowe naprężenie zginające działające na przekrój w wyniku siły skurczowej. Wartość ta jest szczególnie istotna w stanie zarysowanym, gdzie strefa rozciągana betonu nie przenosi już żadnych obciążeń.

M_sh,II = 44,532 kN ⋅ 123,2 mm = 5,48 kNm

Współczynnik krzywizny dla stanu zarysowanego, k_sh,II , wskazuje, jak silny wpływ na odkształcenie przekroju ma moment skurczowy i inne siły działające na konstrukcję. Uwzględniane są tu moment skurczowy M_sh,II, istniejący moment zginający My_,Ed,def oraz siła osiowa N_Ed i jej mimośród e_II. Obliczenia umieszcza moment wynikowy proporcjonalnie do momentu bez skurczu, a tym samym jest miarą wpływu siły skurczowej.

k_sh,II = ( 5,48 kNm + 18,50 kNm - 0 )/( 18,50 kNm - 0 ) = 1,296

Odkształcenie przekroju

Odkształcenie przekroju jest to zakrzywienie elementu konstrukcyjnego spowodowane oddziaływaniami zewnętrznymi, uwzględniające jego parametry materiałowe i stanowe.

Obliczenia odkształcenia przekroju w stanie niezarysowanym, κ_I , opisują zakrzywienie przekroju spowodowane momentem skurczowym i właściwościami sprężystymi materiału. Uwzględniany jest moment skurczowy My_,Ed,def oraz siła osiowa_NEd i jej mimośród e_I. Wartości te są mnożone przez współczynnik k_sh,I opisujący wpływ momentu skurczowego w stanie niezarysowanym. W mianowniku zachodzi efektywny moduł sprężystości betonu', E_c,eff oraz moment bezwładności przekroju niezarysowanego I_I, które określają sztywność przekroju'.

κ_I = (1,161 ⋅ (18,50 kNm - 0))/(10 001,2 MN/m² ⋅ 70 844,30 cm⁴)
= 3 mrad/m

Obliczenia odkształcenia przekroju w stanie zarysowanym, κ_II , pokazują krzywiznę przekroju po zarysowaniu, z uwzględnieniem momentu skurczowego i obniżonej wytrzymałości zarysowanego przekroju. Tutaj moment skurczu My_,Ed,def, siła osiowa_NEd i jej mimośród e_II zostają pomnożone przez współczynnik k_sh,II, opisujący wpływ momentu skurczowego w stanie zarysowanym. W mianowniku traci się efektywny moduł sprężystości betonu E_c,eff oraz zredukowany moment bezwładności zarysowanego przekroju I_II, które odzwierciedlają ten przekrój w mniejszym stopniu's sztywność. Odkształcenie przekroju w stanie zarysowanym jest znacznie większe niż w stanie niezarysowanym, ponieważ sztywność zarysowanego przekroju jest zmniejszona.

κ_II = (1,296 ⋅ (18,50 kNm - 0))/(10 001,2 MN/m² ⋅ 16 933,50 cm⁴) = 14,2 mrad/m

Stan końcowy

Stan końcowy opisuje maksymalne naprężenia, które mogą wystąpić w przekroju niezarysowanym zarówno pod wpływem obciążeń długotrwałych, jak i krótkotrwałych, w celu zapewnienia nośności i użytkowalności elementu konstrukcyjnego.

Maksymalne naprężenie w stanie niezarysowanym pod obciążeniem długotrwałym, σ_max, Określa maksymalne naprężenie, które może wystąpić w przekroju niezarysowanym w wyniku obciążenia długotrwałego. Składa się z dwóch części:

• udział sił osiowych_NEd i_Nsh
• udział momentów zginających My_,Ed,def, Msh_,I oraz momentu wynikającego z mimośrodu (z_I - h/2) siły osiowej_NEd.

Druga część jest wzmocniona przez moment bezwładności I_I i odległość (h - z_I ).

Maksymalne naprężenie w stanie niezarysowanym pod obciążeniem krótkotrwałym, σ_max,st, wskazuje na największe naprężenie w przekroju pod obciążeniem krótkotrwałym. W przeciwieństwie do obciążenia długotrwałego, uwzględniane są tylko siły osiowe_NEd i My_,Ed,def, ponieważ nie występują siły wewnętrzne od skurczu.

Maksymalne naprężenie w stanie niezarysowanym, σ_max , jest większą z dwóch wartości naprężeń spowodowanych obciążeniem długotrwałym i krótkotrwałym. Zapewnia to uwzględnienie największego możliwego obciążenia przekroju.

σ_max = max ( 3.155 MN/m²; 2.689 MN/m² )
= 3,155 MN/m²

Współczynnik rozkładu (parametr uszkodzenia) ζ_d opisuje przejście między zachowaniem się przekroju w stanie niezarysowanym i zarysowanym. Oblicza się ją jako stosunek wytrzymałości charakterystycznej betonu na rozciąganie f_ctm do naprężenia maksymalnego σ_max. W tym przypadku nieliniowość jest uwzględniana przez relację wykładniczą.

ζ_d = 1 – 0,5 ⋅ (2,200 MN/m²/3,155 MN/m²)²
= 0,757 ≤ 1
gdzie:
β = 1,0 (obciążenie krótkotrwałe)
β = 0,5 (obciążenie długotrwałe lub wiele cykli obciążenia powtarzalnego)
Jeżeli współczynnik rozkładu ζ_d = 1, element konstrukcyjny jest całkowicie w stanie zarysowanym. Z drugiej strony, jeśli ζ_d jest równe 0, beton jest całkowicie niezarysowany.

Przy obliczaniu współczynnika rozkładu ζ_d ważne jest, która opcja zostanie wybrana w celu wykrywania stanu zarysowania. W przypadku wybrania opcji 'Stan zarysowania obliczony z obciążenia powiązanego' stan zarysowania (współczynnik rozkładu ζ_d ) jest obliczany wyłącznie na podstawie bieżącego obciążenia (kombinacji obciążeń), jak w tym przykładzie. Pozostałe opcje są opisane w instrukcji.

Zakrzywienie przekroju κ_f jest obliczane poprzez interpolację stanu zarysowanego (κ_II ) i niezarysowanego (κ_I ), ważonych współczynnikiem rozkładu ζ_d. Pozwala to na realistyczny opis zachowania się krzywizny w stanie przejściowym.

κ_f = 0,757 ⋅ 14,2 mrad/m + (1 – 0,757) ⋅ 3 mrad/m
= 11,5 mrad/m
Idealne pole przekroju A_f opisuje przejście między polem przekroju niezarysowanego A_I a zarysowanym A_II. Ponownie ważenie odbywa się na podstawie współczynnika rozkładu, ζ_d.


Idealny moment bezwładności I_y,f opisuje moment przekroju z uwzględnieniem współczynnika rozkładu ζ_d oraz momenty bezwładności w stanie niezarysowanym I_I oraz w stanie zarysowanym I_II. Dodatkowe współczynniki, takie jak k_sh,II i k_sh,I uwzględniają efekty skurczu w odpowiednim stanie.


Mimośród środka ciężkości_ef opisuje położenie wypadkowego środka ciężkości przekroju w oparciu o przejście ze stanu niezarysowanego w stan zarysowany. Uwzględnia on współczynnik rozkładu ζ_d, a także odpowiednie moduły sprężystości E_{c, eff} oraz momenty bezwładności I_I oraz I_II.


Idealny moment bezwładności względem geometrycznego środka przekroju I_y,0,f uwzględnia, oprócz idealnych momentów bezwładności I_y,f oraz idealnego pola przekroju A_f, również przesunięcie środka ciężkości od mimośrodu e_f. Przemieszczenie to jest uwzględniane przez składową Steinera A_f.

I_y,0,f = 16.145,50 cm⁴ + 678,30 cm² ⋅ (-49,2 mm)²
= 32 538,80 cm⁴

Sztywność końcowa

Sztywności końcowe elementu konstrukcyjnego opisują jego odporność na odkształcenia i obrót pod wpływem różnych typów obciążeń. Program uwzględnia sztywność osiową i na zginanie, skręcanie oraz sztywność na ścinanie. Wartości te są wykorzystywane jako podstawa do analizy zachowania konstrukcyjnego i użytkowalności elementu konstrukcyjnego.
Styczna sztywność membranowa EA_f opisuje sztywność osiową przekroju z uwzględnieniem efektywnego modułu sprężystości betonu's E_c,eff i idealnego pola przekroju A_f.

EA_f = 10 001,2 MN/m² ⋅ 678,30 cm²
= 678 387 kN
Sztywność styczna na zginanie, EI_y,0,f , opisuje wytrzymałość przekroju na zginanie względem idealnego środka ciężkości. Jest on określany przez efektywny moduł sprężystości betonu E_c,eff oraz moment idealny powierzchni I_y,0,f.

EI_y,0,f = 10 001,2 MN/m² ⋅ 32 538,80 cm⁴
= 3 254,28 kNm²
Nośność na zginanie przy stycznej, EI_z,0,f , opisuje wytrzymałość przekroju na zginanie względem lokalnej osi z. Jest ona zdefiniowana przez efektywny moduł sprężystości betonu's E_c,eff oraz moment bezwładności wokół osi z I_z.

EI_z,0,f = 10 001,2 MN/m² ⋅ 1 666 670 cm⁴
= 166 687 kNm²

Współczynnik r opisuje redukcję sztywności na ścinanie w oparciu o stosunek idealnych momentów bezwładności I_f oraz I_I.

r = 16145,50 cm⁴/70 844,30 cm⁴
= 0,228
Sztywność na ścinanie względem osi y GA_y,f uwzględnia efektywny moduł ścinania przy ścinaniu ' betonu G_c,eff, pole przekroju Ac_,y oraz współczynnik redukcyjny r.

GA_{y, f} = 4 167,18 MN/m² ⋅ 1 666,67 cm² ⋅ 0,228
= 158 284 kN
Sztywność na ścinanie w kierunku osi z, GA_z,f , oblicza się w taki sam sposób, jak dla osi y.

GA_{z, f} = 4 167,18 MN/m² ⋅ 1 666,67 cm² ⋅ 0,228
= 158 284 kN
Sztywność na skręcanie GI_T,f odpowiada w rozpatrywanym przypadku sztywności na skręcanie w stanie niezarysowanym GI_T,I.

GI_T,f = 7770 kNm²
Element sztywności mimośrodowej ES_y opisuje dodatkowe obciążenie przekroju wywołane mimośrodem e_f. Jest ona obliczana na podstawie sztywności osiowej EA_f oraz mimośrodu e_f.

ES_y = 678 387 kN ⋅ ( -49,2 mm )
= -33 350,20 kNm

Ugięcie

W celu sprawdzenia stanu granicznego użytkowalności rzeczywiste odkształcenie porównywane jest z dopuszczalnymi wartościami granicznymi. Całkowite ugięcie wokół wygięcia wstępnego jest korygowane i sprawdzane z określonymi wartościami granicznymi.
Główna kombinacja obciążeń jest brana pod uwagę przy obliczaniu ugięcia bez efektów zależnych od czasu, takich jak pełzanie i skurcz (krótkotrwałe), podczas gdy odpowiednie kombinacje obciążeń są zawsze obliczane z właściwościami zależnymi od czasu (długotrwałe). Jeżeli dostępne jest więcej niż jedno obciążenie, jako podstawę przyjmuje się ugięcie obciążenia o największej wartości.
Ugięcie graniczne w kierunku z uz_,lim jest obliczane przy użyciu długości referencyjnej w kierunku z L_z,ref i kryterium ugięcia granicznego L_z,ref/u_z,lim.

u_z,lim = 4,210 m/250 = 16,8 mm
Ugięcie w kierunku z,_uz , wynika z różnicy ugięcia całkowitego uz_,tot i wygięcia wstępnego w miejscu x,_uz,c.

u_z = 19,4 mm - 0 = 19,4 mm

Obliczenia

η = maks. (19,4 mm/16,8 mm; 0,0 mm/16,8 mm) = 1,155 Ponieważ η = 1,155 > 1, dopuszczalne ugięcie zostało przekroczone!

Uwagi końcowe

Obliczenia deformacji zgodnie z metodami aproksymacyjnymi zdefiniowanymi w normach, takimi jak analiza deformacji zgodnie z sekcją 7.4.3 normy EN 1992-1-1, są przeprowadzane przy użyciu sztywności efektywnych, które są obliczane w elementach skończonych zgodnie ze stanem granicznym (zarysowany lub niezarysowany). Sztywności efektywne stanowią podstawę do dalszych obliczeń odkształcenia elementu konstrukcyjnego w dalszej analizie MES.

Przekrój z betonu zbrojonego jest uwzględniany przy wyznaczaniu sztywności efektywnych, przy czym przekrój z betonu zbrojonego jest klasyfikowany jako „zarysowany” lub „niezarysowany” dla stanu granicznego użytkowalności na podstawie wyznaczonych sił wewnętrznych. Wpływ betonu między rysami jest uwzględniany za pomocą współczynnika rozkładu, na przykład zgodnie z równaniem 7.19 (EN 1992-1-1). Zakłada się, że zachowanie materiałowe betonu jest liniowo-sprężyste do wytrzymałości betonu na rozciąganie, która jest wystarczająco precyzyjna dla stanu granicznego użytkowalności.

Długotrwałe efekty pełzania i skurczu są uwzględniane podczas określania sztywności efektywnych na poziomie przekroju elementu konstrukcyjnego, w celu zapewnienia realistycznego odwzorowania odkształceń pod wpływem obciążeń długotrwałych.