RF-CONCRETE Columns

什么是受弯组合？

通过系统 (M_G0, N) 指定在点 C 的受弯，称为压力中心。 距离 G₀ C 称为外力相对于纯混凝土截面重心 G₀的偏心。

在组合受弯时，弯矩的大小只取决于该点，这里为 G₀ 。

在组合受弯分析中，首先通过计算e₀找到压力重心。

U' 坐标系考虑几何缺陷和二阶效应

在进行构件和结构分析时，必须考虑结构中任何几何缺陷以及荷载分布时的不利影响。 材料的分项系数通常考虑截面'尺寸的偏差。

孤立单元的长细比和有效长度

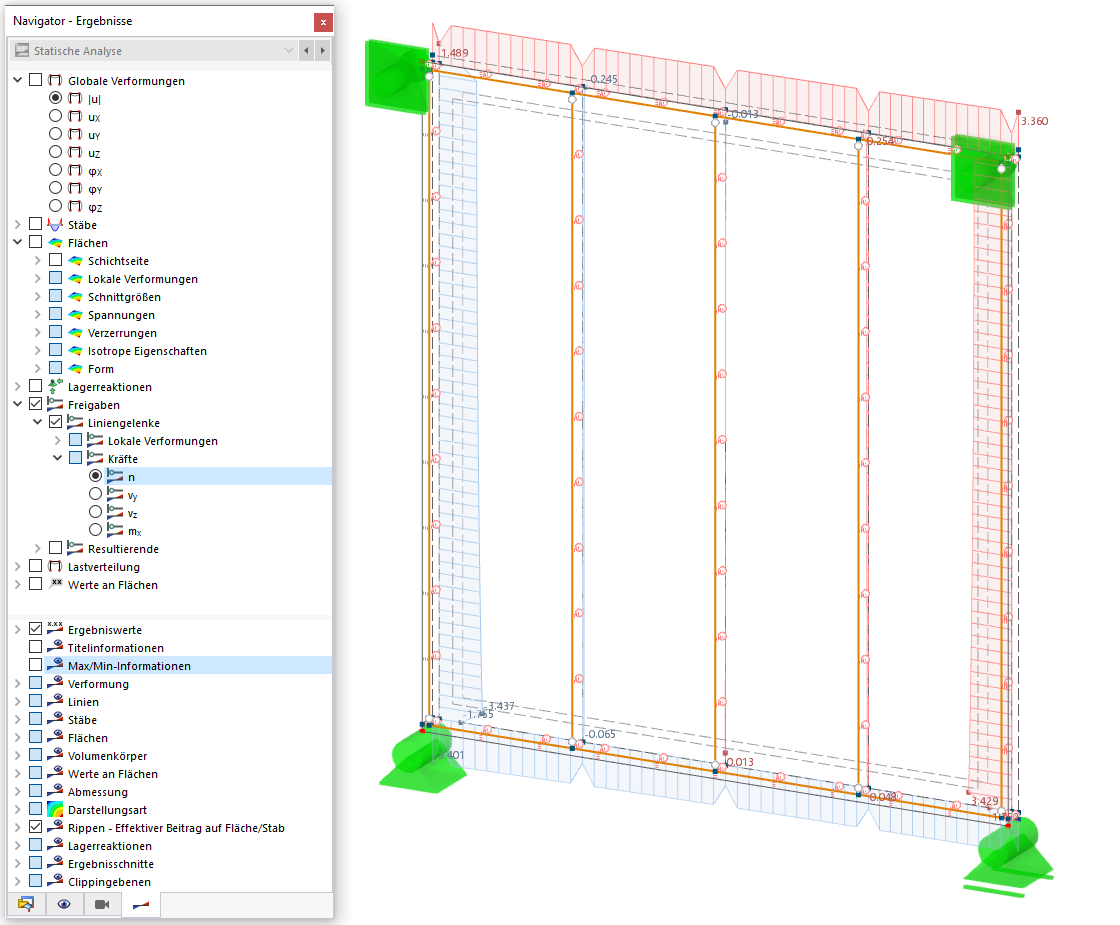
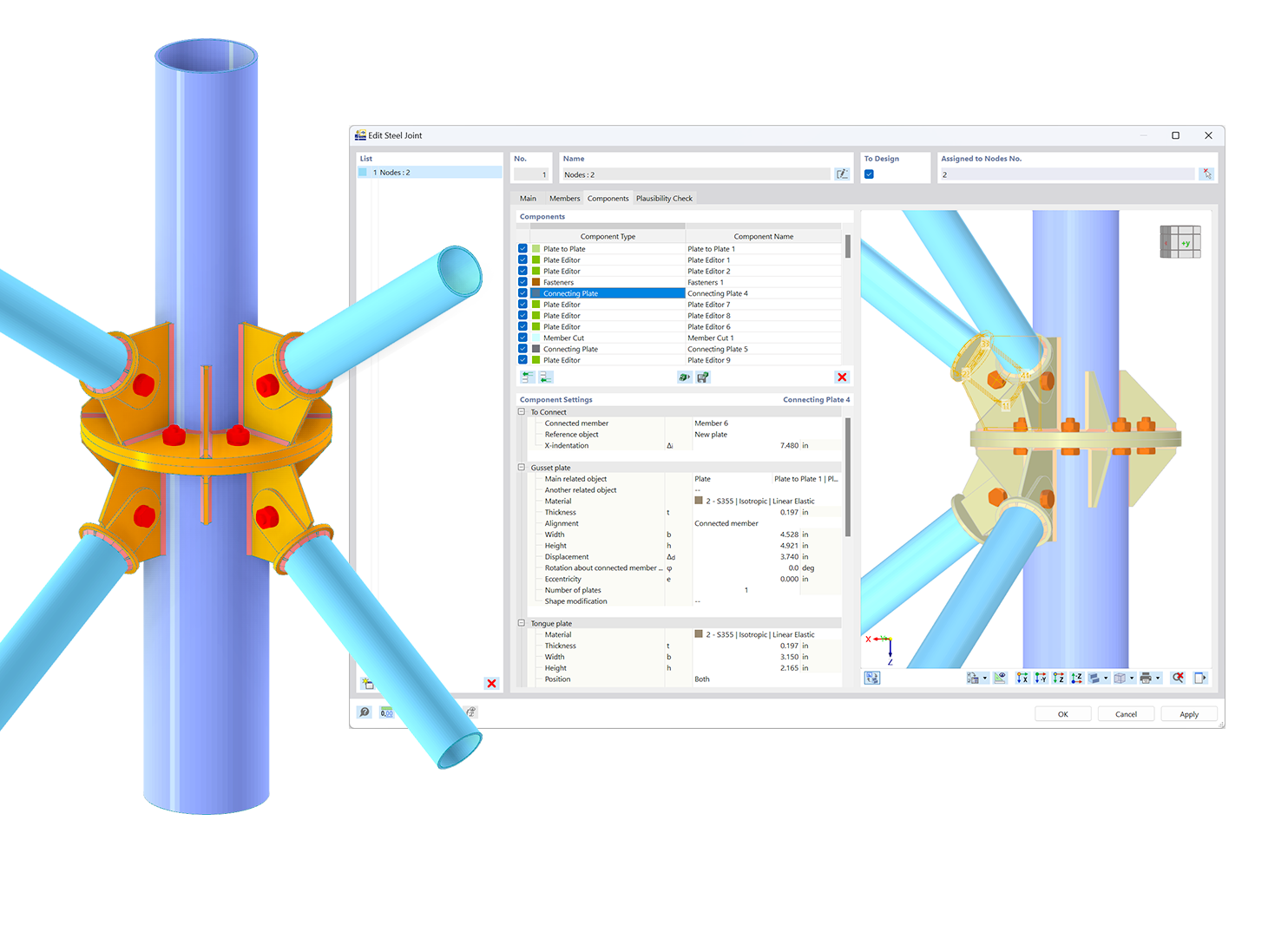
图01显示了在RF-CONCRETE Columns中通过模拟等截面构件的支座条件和自由长度l来选择屈曲长度系数β的可能性。

1 Y轴屈曲长度系数预设值

孤立单元的长细比准则

如果长细比系数小于长细比的准则，那么二阶效应可以忽略。

考虑徐变

在二阶分析中必须考虑徐变的影响，简化地考虑徐变的一般情况和不同荷载的作用持续时间，使用有效的徐变系数。

2 输入数据中的蠕变参数

墙和独立支撑结构柱

对于孤立单元，缺陷的影响可以通过偏心 e_i来考虑。

截面为对称配筋的直截面

考虑到截面尺寸的偏差，弯矩的 ULS 计算方式为：

使用相关性关系图进行钢结构计算

弯矩-轴力关系图适用于快速设计或验算事先确定形状和钢筋分布的平直截面。 相关性图表只是承载能力极限状态。 绘制相互作用图时使用的两条曲线构成连续、封闭的等高线，称为相互作用曲线。 结果中的合力公式和合力矩公式与下列参数有关：

• 混凝土和钢筋变形图
• 混凝土和钢筋应力图

因此，对于给定的截面（混凝土、钢筋、钢筋位置），数量的大小是无量纲的，基于设计内力 N_Ed和 M_EdG0。

最后一个公式允许我们通过使用简化正交坐标系 (μ, υ) 对相互作用曲线的曲线场 ρ 进行插值来确定所需的钢筋截面。

理论与模块 RF-CONCRETE Columns 的比较

我们将通过一个简单的例子将 RF-CONCRETE Columns 的计算结果与之前介绍的理论公式进行比较。

• 施加在有支撑结构的一个纯混凝土重心上的荷载：
  • 永久:
    • N_g = 85 kN
    • M_g = 90 kN.m
  • 可变：
    • _Nq= 75kN
    • M_q = 80kNm
• 材料：
  • C 25/30 混凝土
  • 钢筋： 500
• 柱脚弯矩比:
  • |M01：| / |M02| = 1/3

• 3D Viewer | Google
• 3D Viewer | Babylon
• 虚拟现实

3 RFEM模型中的永久荷载

材料特性

f_cd = 1 ⋅ 25/1.5 = 16.67 MPa

f_yd = 500/1.15 = 434.78 MPa

承载力极限状态

承载能力极限状态下的计算:
M_Ed = 1.35 ⋅ M_g + 1.5 ⋅ M_q
M_Ed = 1.35 ⋅ 90 + 1.5 ⋅ 80 = 241.50 kNm
N_Ed = 1.35 ⋅ N_g + 1.5 ⋅ N_q
N_Ed = 1.35 ⋅ 85 + 1.5 ⋅ 75 = 227.25 kN

4 显示主导荷载

ULS 中考虑无二阶效应的几何缺陷

独立单元的几何长细比，考虑插入基础块中并由梁约束的柱子：
l₀ = ²/2 ⋅ l = ²/2 ⋅ 6,00 = 4,24 m

5 用户自定义输入数据中的屈曲系数

平行于侧面 h = 55 cm 的平面内的惯性矩
i_y = h/12 = 0,55/12 = 0,159 m

平行于侧面 h = 24 cm 的平面内的惯性矩
i_z = b/12 = 0,24/12 = 0,069 m

长细比
λ_y = 4,24/0,159 = 26,67 m
λ_z = 4,24/0,069 = 61,45 m

6 显示长细比值

极限长细比：
默认情况下程序的值 A 是考虑徐变影响影响效应的值，B 是模块在 RF-CONCRETE 中定义的初始配筋的数量，C 是顶部和底部的弯矩比。 但是，可以自己定义这些值：
A = 0.7
B = 1.1
C = 1,7 - 1/3 = 1,37
n = (227.25 ⋅ 10^-3 )/(0.24 ⋅ 0.55 ⋅ 16.67) = 0.103
限制膜_λ = (20 ⋅ 0.7 ⋅ 1.1 ⋅ 1.37)/²(0.103) = 65.74
λ_y < λ_lim ⟘ XZ 平面上的弯矩组合计算
λ_z < λ_lim ⟘ 计算（在 XY 平面简受压）

7 显示长细比极限

在下列偏心应力下，如果长细比系数小于极限值，那么对构件进行屈曲验算是无意义的，并且进行组合弯曲计算就足够了，而不考虑二阶效应：
e₀ = e₁ + e_i

计算荷载引起的偏心
e₁ = M_Ed/N_Ed
e₁: 计算荷载引起的偏心
e₁ = 241.50/227.25 = 1.063 m

为组合弯矩计算考虑荷载修正

来自支撑结构的孤立柱：
θ₀ = 1/200
α_h = 2/6 = 0.816
α_m = ²0,5 ⋅ (1 + 1/1) = 1
θ_i = 0.816 ⋅ 1/200 = 0.0041
e_i = 0.0041 ⋅ 4.24/2 = 0.0087 m

8 偏心计算的详细信息

施加在纯混凝土截面重心上的荷载

e₀ = e₁ + e_i ≥Δe₀
e₀ = 1.063 + 0.0087 = 1.072 m

考虑最小偏心距。
M_EdG0 = 227.25 ⋅ 1.072 = 243.61 kNm

9 显示由于偏心引起的弯矩

对称钢筋矩形截面在受弯构件中的相互作用图

ν_Ed = (227,25 ⋅ 10^-3 )/(0,24 ⋅ 0,55 ⋅ 16,67) = 0,103
μ_Ed = (243.61 ⋅ 10^-3 )/(0.24 ⋅ 0.55² ⋅ 16.67) = 0.201

在相关性图表的图表中可以找到根据折减的力 ν_Ed 、μ_Ed确定所需钢筋的相关性图表（Jean Perchat, Traité de béton armé, LE^MONITEUR第三版, 法国, 2017）。

在图形输出中，在相关曲线 ρ = 0.35 和 ρ = 0.40 之间内插计算得出的值，得出 ρ = 0.375。
A_s = (0.375 ⋅ 0.24 ⋅ 0.55 ⋅ 16.67)/(434.78) ⋅ 10⁴ = 18.98 cm²

10 由RF-CONCRETE Columns确定的所需钢筋

钢筋的 0.10 cm² 差异是计算机对相互作用图表值的插值精度引起的。

知识库

KB 001705 | RF-CONCRETE Columns中组合荷载作用下的混凝土柱计算

知识库

KB 001710 | 使用RF-CONCRETE杆件设计轴心受压混凝土柱。

知识库

KB 001712 | RF-CONCRETE Columns