10697x

001705

M.Eng. Milan Gérard

2021-02-05

Calcolo dei pilastri in calcestruzzo sottoposti a flessione combinata con RF-CONCRETE Columns

Questo articolo tratta gli elementi relativi ai quali la sezione trasversale è soggetta contemporaneamente a un momento flettente, una forza di taglio e una forza di compressione o trazione assiale. Tuttavia, nel nostro esempio non includeremo il carico dovuto alla forza di taglio.

Cos'è la flessione combinata?

La flessione combinata è indicata dal sistema (M_G0, N) applicato in un punto C, chiamato centro di pressione. La distanza G₀ C è chiamata eccentricità della forza esterna rispetto al baricentro G₀ della sezione di calcestruzzo puro.

Nella flessione combinata, il valore del momento flettente dipende quindi solo da questo punto, dove viene eseguita la riduzione delle forze; qui, è G₀.

e_{0} = \frac{M_{{EdG}_{0}}}{N_{Ed}}

e₀	eccentricità rispetto al baricentro della sezione di calcestruzzo puro
Θ	Coefficiente di stabilità
C_{[CRASHREASON.DESCRIPTION]}	Fattore di amplificazione della deformazione secondo la Tabella 12.2-1

Eccentricità in relazione al centro di gravità della sezione di calcestruzzo puro

La prima cosa da fare nella flessione combinata è trovare la posizione del centro di pressione calcolando e₀.

Considerazione delle imperfezioni geometriche e degli effetti del secondo ordine in U'

L'analisi di elementi e strutture deve tenere conto degli effetti sfavorevoli di eventuali imperfezioni geometriche nella struttura, nonché delle deviazioni nella posizione dei carichi. Le deviazioni nelle dimensioni delle sezioni' sono normalmente prese in considerazione dai coefficienti parziali di sicurezza per i materiali.

Snellezza e lunghezza efficace di elementi isolati

λ = \frac{l_{0}}{i}

l_{0} = β \cdot l

λ	coefficiente di snellezza
l₀	lunghezza efficace determinata
i	raggio di rotazione della sezione di calcestruzzo non fessurata
β	coefficiente della lunghezza di instabilità
i_e	Fattore di importanza, definito nella sezione 11.5.1

Coefficiente di snellezza

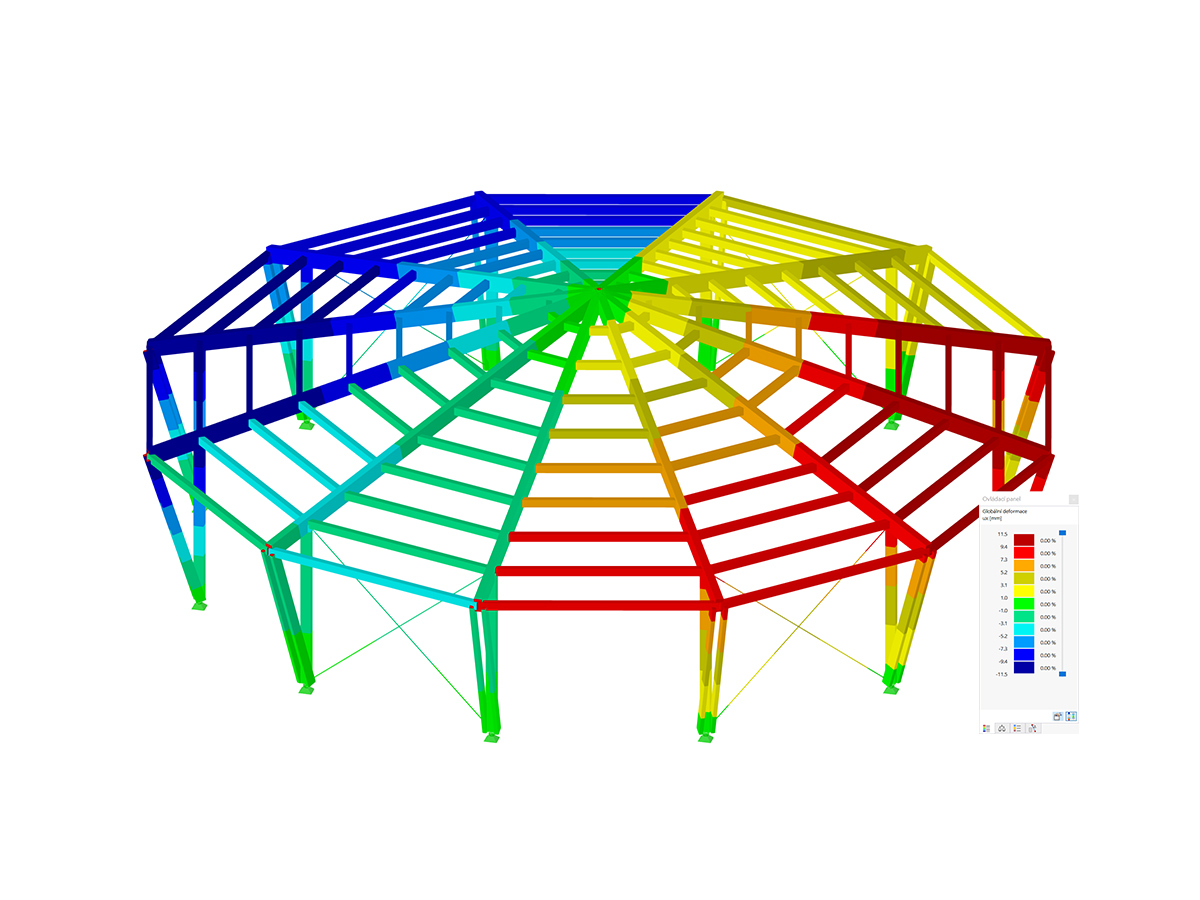
L'immagine 01 mostra la possibilità in RF-CONCRETE Columns di selezionare il coefficiente di lunghezza di instabilità β mediante modellazione delle condizioni di vincolo di elementi isolati con sezione costante e lunghezza libera l.

1 Valori predefiniti del coefficiente di lunghezza di instabilità attorno all'asse Y.

Criterio di snellezza per elementi isolati

Si presume che gli effetti del secondo ordine possano essere trascurati se si verifica che il coefficiente di snellezza è inferiore al criterio di snellezza.

λ < λ_{\lim}

λ_{\lim} = \frac{20 \cdot A \cdot B \cdot C}{\sqrt{n}} selon l ’ AN française

A = \frac{1}{1 + 0, 2 \cdot φ_{ef}} = 0, 7 si φ_{ef} est inconnu

B = \sqrt{1 + 2 \cdot ω} = 1, 1 si ω est inconnu

C = 1, 7 - r_{m} = 0, 7 si r_{m} est inconnu

n = \frac{N_{Ed}}{A_{C} \cdot f_{cd}}

r_{m} = \{\begin{cases} 1, si éléments non contreventés en général \\ 1, si éléments contreventés avec moments du premier ordre dus principalement à des imperfections ou à des charges transversales \\ \frac{M_{01}}{M_{02}} \leq 1, si autres cas \end{cases}

λ	criterio di snellezza
λ_lim	snellezza limite
φ_ef	coefficiente di viscosità efficace
ω	percentuale di armatura meccanica
r_m	rapporto dei momenti
M₀₁ , M₀₂	valori algebrici dei momenti del primo ordine ad entrambe le estremità dell'elemento

Criterio di snellezza

Considerazione della viscosità

L'effetto della viscosità deve essere preso in considerazione nell'analisi del secondo ordine, considerando sia le condizioni generali di viscosità che la durata dell'applicazione di diversi carichi in modo semplificato utilizzando un coefficiente di viscosità efficace.

φ_{ef} = φ (\infty, t_{0}) \cdot \frac{M_{0 E_{qp}}}{M_{0 Ed}}

φ_ef	coefficiente di viscosità efficace
φ (∞, t₀ )	valore finale del coefficiente di viscosità
M_0Eqp	momento di servizio del primo ordine sotto una combinazione quasi permanente di azioni
M_0Ed	momento ultimo del primo ordine in combinazione di carichi di progetto (comprese le imperfezioni geometriche)

Coefficiente di viscosità efficace

2 Parametri di scorrimento nei dati di input

Pareti e colonne isolate di strutture controventate

Nel caso di elementi isolati, l'effetto delle imperfezioni può essere considerato come eccentricità e_i.

e_{i} = θ_{i} \cdot \frac{l_{0}}{2}

θ_{i} = θ_{0} \cdot α_{h} \cdot α_{m}

θ_{0} = \frac{1}{200}

\frac{2}{3} \leq α_{h} = \frac{2}{\sqrt{l}} \leq 1

α_{m} = \sqrt{0, 5 \cdot (1 + \frac{1}{m})}

e_i	eccentricità dovuta a imperfezioni
θ_e	inclinazione complessiva della struttura
θ_{[LinkToImage04]}	valore di base raccomandato da NA
α_h	coefficiente di riduzione relativo alla lunghezza
α_m	coefficiente di riduzione relativo al numero di elementi dove m è il numero di elementi verticali che contribuiscono all'effetto totale

Eccentricità dovuta a imperfezioni

Sezioni trasversali diritte con armatura simmetrica

Per tenere conto delle deviazioni nelle dimensioni delle sezioni trasversali, il momento flettente dovrebbe essere calcolato in SLU:

M_{E {dG}_{0}} = M_{Ed} + N_{Ed} \cdot ∆ e_{0}

∆ e_{0} = Ma x \{\begin{cases} 20 mm \\ \frac{h}{30} : excentricité minimale requise \end{cases}

M_EdG0	Momento flettente
M_Ed	Valore di progetto del momento flettente
Δe_{[LinkToImage04]}	eccentricità minima richiesta
h	altezza della sezione diritta nel piano di flessione

Momento flettente

Calcolo degli acciai utilizzando i 'diagrammi di interazione

I diagrammi di interazione della forza momento-normale sono grafici che consentono la progettazione rapida o la verifica di sezioni trasversali diritte di cui la forma e la distribuzione dell'armatura sono determinate in anticipo. I diagrammi di interazione sono stabiliti solo per lo stato limite ultimo. Un diagramma di interazione viene disegnato utilizzando 2 curve che costituiscono un contorno continuo e chiuso chiamato curva di interazione. L'andamento di queste curve si basa sulle equazioni della risultante e del momento risultante, a seconda in particolare dei seguenti parametri:

Diagrammi di deformazione del calcestruzzo e dell'acciaio
Diagrammi delle tensioni del calcestruzzo e dell'acciaio

Pertanto, per la sezione trasversale data (calcestruzzo, armatura, posizione dell'acciaio di armatura), le quantità sono definite senza dimensione, in base alle forze interne di progetto N_Ed e M_EdG0.

ν_{Ed} = \frac{N_{Ed}}{A_{c} \cdot f_{cd}}

A_{c} = b \cdot h

ν_Ed	forza assiale ridotta
A_c	superficie totale della sezione in calcestruzzo puro
b	larghezza della sezione diritta nel piano di flessione
f_cd	valore di progetto della resistenza a compressione del calcestruzzo

Forza assiale ridotta

μ_{Ed} = \frac{M_{{EdG}_{0}}}{A_{c} \cdot h \cdot f_{cd}}

μ_Ed	momento flettente ridotto in G₀

Momento flettente ridotto in G0

ρ = \frac{A_{s} \cdot f_{yd}}{A_{c} \cdot f_{cd}}

ρ	percentuale meccanica di armatura
A_s	area di armatura
f_yd	tensione di snervamento di progetto dell'acciaio per cemento armato

Percentuale meccanica di armatura

L'ultima equazione ci consente di determinare la sezione di armatura necessaria interpolando i campi della curva ρ del diagramma di interazione, utilizzando il sistema di coordinate ortonormali ridotto (μ, υ).

Confronto della teoria con il modulo aggiuntivo RF-CONCRETE Columns

Utilizzando un semplice esempio, confrontiamo i risultati in RF-CONCRETE Columns con le formule teoriche descritte in precedenza.

Carico applicato al baricentro del calcestruzzo puro, di un elemento di una struttura controventata:
- Permanente:
  - N_g = 85 kN
  - M_g = 90 kN.m
- Variabile:
  - _Nq = 75 kN
  - _Mq = 80 kNm
Materiali:
- Calcestruzzo C 25/30
- Acciaio: S 500
Rapporto del momento alla base della colonna:
- |M01:| / |M02| = 1/3

3 Modello RFEM con carichi permanenti modellati

Caratteristiche del materiale

f_{cd} = α_{cc} \cdot \frac{f_{ck}}{γ_{c}}

f_cd	Valore di progetto della resistenza a compressione del calcestruzzo
α_cc	Coefficiente che tiene conto degli effetti a lungo termine sulla resistenza a compressione
f_ck	resistenza caratteristica a compressione del calcestruzzo
γ_c	coefficiente parziale di sicurezza relativo al calcestruzzo

Valore di progetto della resistenza a compressione del calcestruzzo

f_cd = 1 ⋅ 25/1,5 = 16,67 MPa

f_{y d} = \frac{f_{y k}}{γ_{s}}

[F5]_yk	tensione di snervamento caratteristica dell'acciaio per armatura
γ_s	coefficiente parziale di sicurezza relativo all'acciaio per armatura

Tensione di snervamento di progetto dell'acciaio di armatura

f_yd = 500/1,15 = 434,78 MPa

capacità portante

Caricamento dei calcoli allo stato limite ultimo:
M_Ed = 1.35 ⋅ M_g + 1.5 ⋅ M_q
M_Ed = 1.35 ⋅ 90 + 1.5 ⋅ 80 = 241.50 kNm
N_Ed = 1.35 ⋅ N_g + 1.5 ⋅ N_q
N_Ed = 1.35 ⋅ 85 + 1.5 ⋅ 75 = 227.25 kN

4 Visualizzazione dei carichi determinanti

Considerazione delle imperfezioni geometriche senza effetti del secondo ordine in SLU

Snellezza geometrica per elementi isolati, considerando la colonna inserita in un blocco di fondazione e vincolata da una trave:
l₀ = √2/2 ⋅ l = √2/2 ⋅ 6,00 = 4,24 m

5 Coefficienti di instabilità definiti dall'utente nei dati di input

Raggio di inerzia nel piano parallelo al lato h = 55 cm
i_y = h/√12 = 0,55/√12 = 0,159 m

Raggio di inerzia nel piano parallelo al lato h = 24 cm
i_z = b/√12 = 0,24/√12 = 0,069 m

Snellezze
λ_y = 4,24/0,159 = 26,67 m
λ_z = 4,24/0,069 = 61,45 m

6 Visualizzazione dei valori di snellezza

Snellezza limitante:
Per impostazione predefinita, il programma considera i valori in base agli effetti della viscosità per A, le armature iniziali definite in RF-CONCRETE Columns per B e il rapporto dei momenti alla testa e alla base dell'asta analizzata per C. Tuttavia, è possibile definire questi valori da soli:
A = 0,7
B = 1.1
C = 1,7 - 1/3 = 1,37
n = (227,25 ⋅ 10^-3 )/(0,24 ⋅ 0,55 ⋅ 16,67) = 0,103
λ_lim = (20 ⋅ 0.7 ⋅ 1.1 ⋅ 1.37)/√(0.103) = 65.74
λ_y < λ_lim ⟹ calcolo combinato di flessione nel piano XZ
λ_z < λ_lim ⟹ calcolo per compressione semplice nel piano XY

7 Visualizzazione dei limiti del rapporto di snellezza

Essendo i coefficienti di snellezza inferiori ai valori limite, è inutile controllare la parte per instabilità ed è sufficiente avere un calcolo per la flessione combinata senza tenere conto degli effetti del secondo ordine, sotto le seguenti tensioni di eccentricità:
e₀ = e₁ + e_io

Eccentricità dovuta al carico computazionale
e₁ = M_Ed/N_Ed
e₁: Eccentricità dovuta al carico computazionale
e₁ = 241,50/227,25 = 1,063 m

Carico corretto per il calcolo della flessione combinata

Pilastro isolato dalla struttura controventata:
θ₀ = 1/200
_αh = 2/√6 = 0,816
α_m = √0.5 ⋅ (1 + 1/1) = 1
θ_i = 0,816 ⋅ 1/200 = 0,0041
e_i = 0,0041 ⋅ 4,24/2 = 0,0087 m

∆ e_{0} = Max \{\begin{cases} 20 mm \\ \frac{50}{30} \end{cases} = Max \{\begin{array}{l} 20 mm \\ 1, 83 mm \end{array} = 20 mm

Sezione diritta con armatura simmetrica

8 Dettagli del calcolo dell'eccentricità

Carico applicato al baricentro della sezione trasversale di calcestruzzo puro

e₀ = e₁ + e_io ≥ Δe₀
e₀ = 1,063 + 0,0087 = 1,072 m

L'eccentricità minima è rispettata.
M_EdG0 = 227.25 ⋅ 1.072 = 243.61 kNm

9 Visualizzazione del momento determinante a causa dell'eccentricità

Diagramma di interazione per una sezione rettangolare con armatura simmetrica in flessione combinata

ν_Ed = (227.25 ⋅ 10^-3 )/(0.24 ⋅ 0.55 ⋅ 16.67) = 0.103
μ_Ed = (243,61 ⋅ 10^-3 )/(0,24 ⋅ 0,55² ⋅ 16,67) = 0,201

Il diagramma di interazione utilizzato per determinare l'armatura necessaria secondo le forze ridotte ν_Ed, μ_Ed è accessibile nei grafici dei diagrammi di interazione (Jean Perchat, Traité de béton armé,^3a edizione di LE MONITEUR, Francia, 2017).

Nell'output grafico, il valore trovato viene quindi interpolato tra le curve di interazione ρ = 0,35 e ρ = 0,40, risultando in ρ = 0,375.
A_s = (0,375 ⋅ 0,24 ⋅ 0,55 ⋅ 16,67)/(434,78) ⋅ 10⁴ = 18,98 cm²