RFEM 中计算钢纤维混凝土的材料属性和工程计算

材料属性

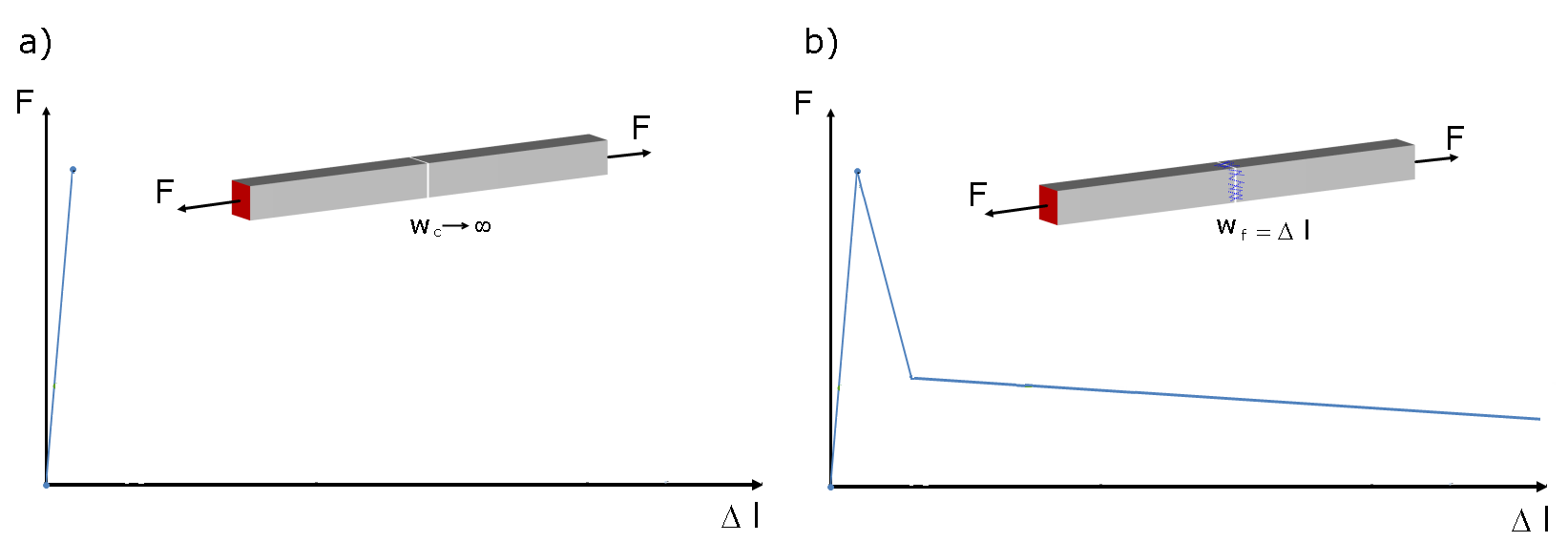
根据规范 DIN EN 206-1，纤维混凝土是指在混凝土中添加钢纤维以达到某些性能。 通过添加足够的钢纤维，可以在混凝土中的裂缝中传递拉力。 图 01 比较了未钢筋混凝土和钢纤维混凝土在受拉时的一般行为。 从图中可以看出，钢纤维混凝土的抗拉承载力随着变形的增加而减小，并且荷载-变形曲线在达到抗拉强度后呈现下降的分支。

1 a）无钢筋混凝土和b）钢纤维混凝土的荷载-变形行为

钢纤维混凝土复合材料在超过混凝土抗拉强度之后的强度称为开裂后抗拉强度。 实际出现在钢纤维上的拉力分布在混凝土受拉区的面积上。 开裂后抗拉强度通常在建筑材料实验室中通过弯曲拉伸试验确定。 使用尺寸 b/h/l = 150 mm/150 mm/700 mm 的钢梁作为试件。由于后开裂区域的抗弯受拉行为对钢纤维混凝土工作线非常重要，所以进行位移可控制的四点抗弯试验。图 02 中显示了四点弯曲试验的尺寸标注。

2 Prüfeinrichtung zur Ermittlung der Nachrissbiegezugfestigkeit (Abmessungen in mm)

四点弯曲试验装置表明裂缝的位置在试验梁上的任意位置，因为在两个荷载点之间的局部荷载是恒定的。 下图显示了最终测试的结果（测试结束后手动伸出压力机以增加裂缝开口），裂缝任意出现在两个压辊之间的主导位置（= 最薄弱的位置） [SCHOOL.INSTITUTION]

3 四点弯曲试验断裂（图： BPLMüllerund Lobisch GmbH）

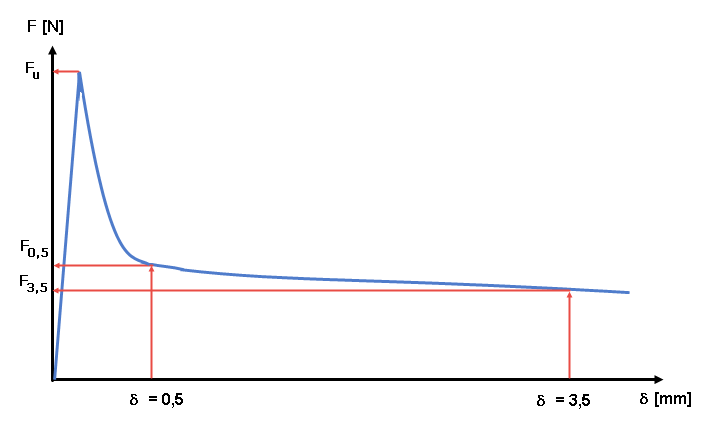
检查结果记录在荷载-变形曲线中（见图 04）。 由该荷载-变形曲线可以确定等效抗拉强度，并且借助换算系数可以确定钢纤维混凝土的开裂后抗拉强度。 A distinction is made between a characteristic value for the evaluation of the serviceability limit state (= small deformations, δ = 0.5 mm) and a governing parameter for the ultimate limit state (= large deformations, δ = 3.5 mm).

4 定义裂缝出现后的抗拉强度的符号荷载-变形曲线

钢纤维混凝土的开裂后抗弯强度在δ = 0.5 mm的情况下由F_0.5和在δ = 3.5mm的荷载值F_3.5确定。 用达到的荷载 L_i （其中 i=0.5 ，相应的值为 3.5）乘以相关的荷载力臂，然后除以未开裂截面的截面模量 W_j 。 由 n 个试件组成的梁的开裂后抗弯强度 f^f_cflm,Li平均值为开裂后抗拉强度值的算术平均值。

为了对钢纤维混凝土复合材料进行分级，在德国钢筋混凝土委员会的钢纤维混凝土指导原则（DAfStb）中规定了两种不同的性能等级：L1和L2。 性能等级 L1 描述小变形 (δ = 0.5 mm) 时的材料属性，性能等级 L2 描述大变形 (δ = 3.5 mm) 时的材料属性。对性能等级 Li 的标注对应于相应变形的开裂后弯曲抗拉强度 f^f_cflk,Li的标准值。裂缝后抗弯抗拉强度标准值是由裂缝后抗弯抗拉平均值 f^f_cflm,Li根据] 计算得出。

因此在钢纤维混凝土的后面标注了字母 L，代表性能等级以及变形 1 (SLS) 和 2 (ULS) 的开裂后抗弯强度标准值。 例如，C30/37 L0.9/L0.6 XC1 钢纤维混凝土，开裂后抗弯抗拉强度标准值，对于变形1，为0.9 N/mm²，在变形2，为0.6 N/mm²。

钢纤维混凝土应力-应变曲线

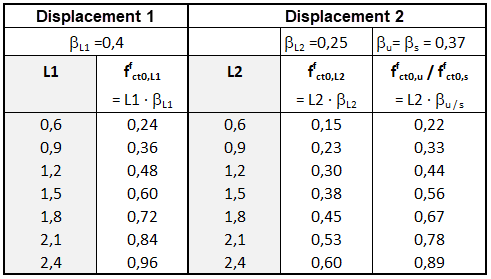
应力-应变曲线在设计钢结构构件时用到。 为此，开裂后抗弯抗拉强度标准值 f^f_cflk,Li方程通过按照中国规范的开裂后抗拉强度 f f cflk,Li 通过系数 β 换算成开裂后抗拉强度 f^f_ct0,i。 %\}]。 根据德国钢筋混凝土结构委员会（DAfStb）的表格 R3 钢筋混凝土纤维混凝土指南 [1] 已经给出了开裂后轴心抗拉强度的基本值 f^f_{ct0， i}代表相应的性能等级（见图 05）。

5 Gebräuchlichste Leistungsklassen L1 und L2 mit zugehörigen Grundwerten der zentrischen Nachrisszugfestigkeit

为了得到应力-应变曲线的计算值 f^f_ctR,i ，我们必须通过两个修正系数 k^f_G和 k^f_F对轴心抗拉强度的基本值进行修正。

钢纤维规范 [1] 的前提是，四点弯曲变形 1 δ = 0.5 mm 对应应变 ε = 0.0035，变形 2 δ = 3.5 mm对应于应变 ε = 0.025。

1. Refer [1]]] 中提到受拉区域时，会根据所进行的计算得出不同的应力-应变曲线。 对于非线性的变形和内力，在受拉区使用图 06 所示的多重线性关系。 在达到混凝土抗拉强度 f_ctm之前，一直应用线性分布。 根据{%！ 当性能等级比率 L2/L1 ≤ 0.7 时，只允许应用应力分布（图 06 中的绿色虚线）。

6 Spannungs-Dehnungs-Linie im Zugbereich nach [1] für die Schnittgrößen- und Verformungsermittlung bei nichtlinearen Verfahren

在承载能力极限状态下的截面设计不允许使用混凝土抗拉强度 f_ctm 。 附加抗拉强度仅来自裂缝中由钢纤维传递的拉力。 此外，承载能力极限状态下的抗拉强度设计值 f^f_ctd,Li验算。 将f^f_ctR,Li的计算值乘以折减系数α^f_c再除以分项系数γ^f_ct得到。 f^f_ctd,L1和f^f_ctd,L2 （图 7中的蓝色实线）的应用限于比值L2/L1≥0.7。 当比值 L2/L1 ≤ 1 时，图 07 中绿色虚线所示的应力分布可以简化计算。

7 Spannungs-Dehnungs-Linie auf der Zugseite gemäß [1] für die Querschnittsbemessung im Grenzzustand der Tragfähigkeit

在钢纤维增强的混凝土的应力-应变曲线的受压区中，没有添加纤维的普通混凝土与钢纤维增强的混凝土之间的区别。 欧洲规范 EN 1992-1-1 {% 查看 4]]] 中的规定同样适用于受压区的应力-应变关系。 因此在对变形和内部结构的非线性计算中建议使用第 3.1.5 章中规定的第 3.1.5 章中的抛物线形图表{%！ {%|#受压区的应力-应变关系参见[4]]]。

8 Spannungs-Dehnungs-Linie nach [4] für den Druckbereich: a) für die nichtlineare Berechnung; b) für die Querschnittsbemessung

使用 RFEM 进行非线性计算

根据{%！ 在所有其他情况下，非线性计算仅适用于具有弹性地基的结构构件，水下锚固混凝土板，桩承式底板，壳形结构构件和整体制造的预制容器。

下面将在 RFEM 中定义钢纤维混凝土的应力-应变曲线，并检查材料性能。 首先，将有限元单元施加在单轴拉力上进行计算。 通过这个简单的试验来验证 RFEM 中使用的材料模型在承受单轴拉力时的性能。

对于钢纤维混凝土内力和变形的非线性计算，根据欧洲规范 EN 1992-1-1 中的 3.1.5，受压区的应力-应变图是由抛物线组成的{%#Refer [4 ]]] ，并且在考虑混凝土抗拉强度 f_ctm的多线性分布的受拉区域内（图06）。 在 RFEM 中必须使用一个材料模型来模拟裂缝在形成之后的扩展过程。 通过附加模块 RF-MAT NL，RFEM 可以通过材料模型“二维/三维各向同性损伤”精确地模拟这种行为。

在之前的文章中已经对材料模型“各向同性损伤”进行了详细介绍：
知识库 001461 | 非线性材料损伤模型

在 RFEM 中通常输入应力-应变曲线 。 用户可以在“图表...”选项中分别定义受压和受拉区域。 只有原点的弹性模量必须与后续受压和受拉各点相同。 参照单元尺寸 l_FE,R保持不变，长度为 0.0 m。 这样确保在计算时损伤区域1:1的按照定义的应力-应变曲线。 图 09 显示的是在 RFEM 输入窗口中输入分析的钢纤维混凝土。

9 Definition der Spannungs-Dehnungs-Linie des Stahlfaserbetons

由于下面需要对开裂后受拉构件进行详细分析，所以下面将对被测试的钢纤维混凝土受拉区域的属性进行说明：

• f_ctm = 2.500 N/mm²
• 1.04 ⋅ f^f_ctr,L1 = 0.862 N/mm²
• 1.04 ⋅ f^f_ctr,L2 = 0.458 N/mm²

根据上述受拉区的材料参数得出图 10 中所示的应力-应变曲线。

10 RFEM中的计算模型： ein FE-Element, links gehalten, rechts gezogen

为了避免相邻单元和双轴应力状态对结果的影响，材料的边长为 1 ⋅ 1 m。 将单元的一侧水平放置，然后在另一侧拉动。 为了获得开裂后抗拉强度像，必须以时间控制的方式施加位移，例如上述的四点弯曲试验。 图11显示的是RFEM中的计算模型。

11 Vorgabe der stufenweise ansteigenden Belastung

在荷载工况的计算参数中使用“逐步增加荷载”选项，变形会一直增加，直到达到中断准则。 所使用的断裂准则定义为节点位移为 25.1 mm，对应于 0.0251 的应变 ε。

12 Darstellung der 1. Membranspannung im Berechnungsdiagramm

沿着主轴 σ_{1,m 的}膜板应力用于计算结果的评估。 在“计算参数”对话框中，可以显示荷载逐步增量的计算结果。

13 Gegenüberstellung der RFEM-Ergebnisse mit definierter Materialeigenschaft im Zugbereich

计算得出的膜应力完全符合开裂后抗拉强度的规定。 下图中，主应力 ma σ_1,m由钢纤维混凝土在受拉区的应力-应变曲线中定义。 RFEM 中计算的结果与定义的工作线完全匹配。

14 Spannungs-Dehnungs-Linie des Stahlfaserbetons im Zugbereich für eine nichtlineare Berechnung

概述总结

使用材料模型“二维/三维各向同性损伤”可以验证钢纤维混凝土在单轴拉力作用下的验算行为。 请注意，对于此类验证计算，所有例如相邻单元、多轴应力状态或材料模型中的应力状态的影响都将通过指定参考单元大小 l_{FE,R 来排除。}

知识库

知识库 001601 | RFEM 中计算钢纤维混凝土的材料属性和工程计算

知识库

知识库 001601 | RFEM 中计算钢纤维混凝土的材料属性和工程计算