Określanie właściwości materiałowych betonu zbrojonego włóknami stalowymi i zastosowanie w programie RFEM

parametry materiału

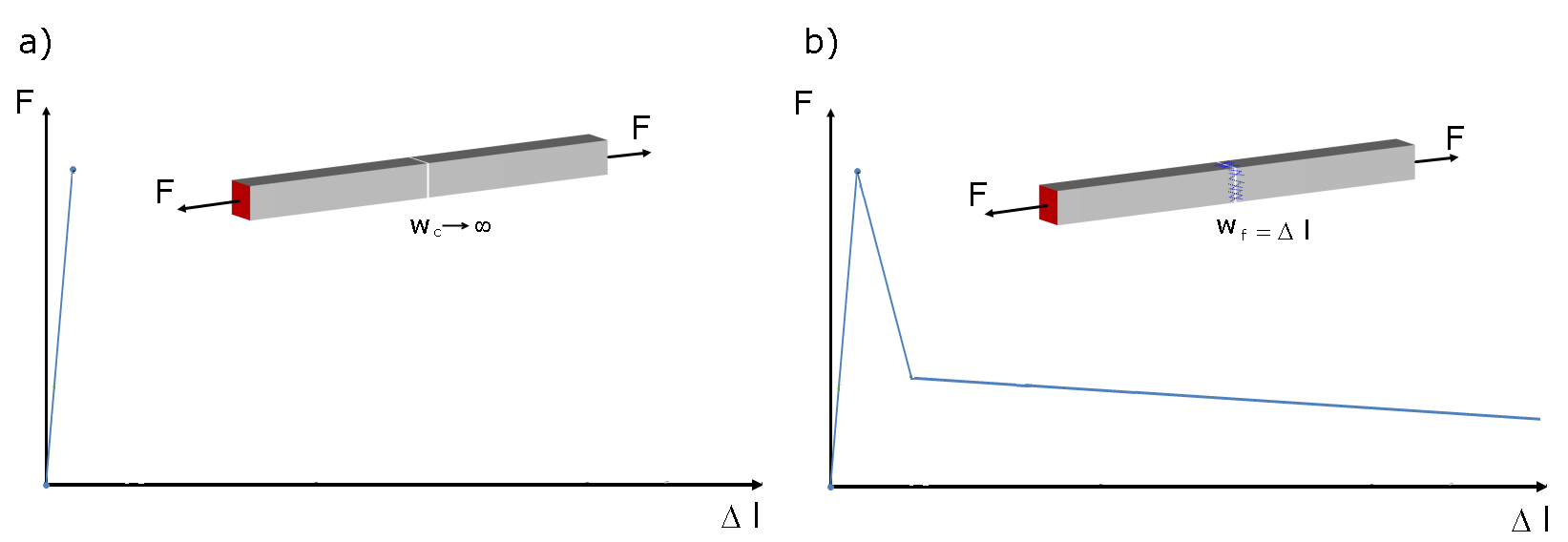
Zgodnie z DIN EN 206-1 beton zbrojony włóknami jest betonem, do którego dodano włókna stalowe w celu uzyskania określonych właściwości. Dzięki dodaniu wystarczającej ilości włókien stalowych, mogą one przenosić siły rozciągające przez rysę w betonie. Rysunek 01 porównuje ogólne zachowanie betonu niezbrojonego i betonu zbrojonego włóknami stalowymi pod wpływem rozciągania. Jak widać, nośność betonu zbrojonego włóknami stalowymi na rozciąganie zmniejsza się wraz ze wzrostem odkształcenia, a krzywa obciążenie-odkształcenie ma opadającą gałąź po osiągnięciu wytrzymałości na rozciąganie.

1 Zachowanie się obciążenia-odkształcenia a) betonu niezbrojonego orazb) betonu zbrojonego włóknami stalowymi

Wytrzymałość kompozytu betonowego zbrojonego włóknami stalowymi po przekroczeniu wytrzymałości betonu na rozciąganie nazywana jest wytrzymałością na rozciąganie po zarysowaniu. Siły rozciągające faktycznie występujące we włóknach stalowych są odniesione do powierzchni rozciąganej strefy betonu. Wytrzymałość na rozciąganie po zarysowaniu jest zazwyczaj określana za pomocą próby rozciągania ze zginaniem, zgodnie z [1], w laboratorium materiałów budowlanych. Jako próbki do badań stosowane są belki o wymiarach b/h/l = 150 mm/150 mm/700 mm. Ponieważ rozciąganie przy zginaniu w rejonie zarysowania jest istotne dla przebiegu pracy betonu zbrojonego włóknami stalowymi, 4-punktowa próba zginania jest przeprowadzana z uwzględnieniem przemieszczeń. Rysunek 02 przedstawia zwymiarowaną reprezentację graficzną testu 4-punktowego zginania.

2 Prüfeinrichtung zur Ermittlung der Nachrissbiegezugfestigkeit (Abmessungen in mm)

Ze względu na układ eksperymentalny 4-punktowej próby zginania, położenie rys na belce testowej jest dowolne, ponieważ obciążenie lokalne między dwoma punktami obciążenia jest stałe. Na poniższym rysunku z testu końcowego (prasa została wydłużona ręcznie, aby zwiększyć rozwarcie rys po zakończeniu testu), rysy powstają arbitralnie między dwoma walcami prasowymi w decydującym miejscu (= najsłabsze położenie).

3 Ukończono 4-punktowy test zginania z otwarciem na rysy (zdj.: BPL Müller and Lobisch GmbH)

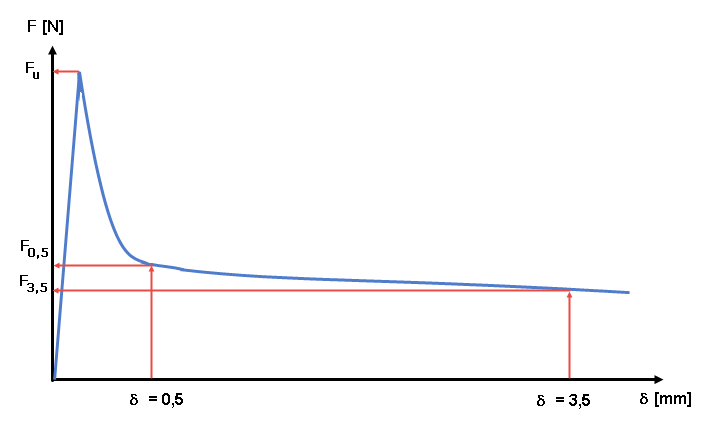
Wyniki badań są udokumentowane w postaci krzywej obciążenia-odkształcenia (patrz Rysunek 04). Na podstawie krzywej obciążenie-odkształcenie określane są równoważne wytrzymałości na rozciąganie oraz, za pomocą współczynników konwersji, wytrzymałość betonu zbrojonego włóknami stalowymi na rozciąganie po zarysowaniu. Rozróżnia się wartość charakterystyczną dla oceny stanu granicznego użytkowalności (= małe deformacje, δ = 0,5 mm) oraz wartość decydującą dla stanu granicznego nośności (= duże deformacje, = 3,5 mm).

4 Symboliczna krzywa obciążenia-odkształcenia do określania wytrzymałości na rozciąganie po zarysowaniu

Wytrzymałości betonu zbrojonego włóknami stalowymi na rozciąganie po zarysowaniu należy określić na podstawie wartości obciążenia F_0,5 dla δ = 0,5 mm i F_3,5 dla δ = 3,5 mm. W tym przypadku, osiągnięte obciążenie L_i (przy i=0,5 oraz odpowiednio 3,5) jest mnożone przez odpowiednie ramię dźwigni obciążenia i dzielone przez moduł przekroju W_j niezarysowanego przekroju. Uśrednioną wytrzymałość na rozciąganie po zarysowaniu^f_cflm,Li dla serii n belek badawczych uzyskuje się jako średnią arytmetyczną wytrzymałości na rozciąganie poszczególnych elementów po zarysowaniu.

W celu sklasyfikowania materiału kompozytowego beton-włókno-stalowe i beton zbrojony, wytyczne dla betonu zbrojonego włóknem stalowym Niemieckiego Komitetu ds. Betonów Zbrojonych (DAfStb) określają dwie różne klasy użytkowania: L1 i L2. Klasa użytkowania L1 opisuje właściwości materiału dla małych odkształceń (δ = 0,5 mm), a klasa użytkowania L2, zachowanie przy większych odkształceniach (δ = 3,5 mm). Opis klas użytkowania Li odpowiada wartości charakterystycznej wytrzymałości na rozciąganie po zarysowaniu^f_cflk,Li w N/mm² dla odpowiednich odkształceń. Charakterystyczną wytrzymałość na rozciąganie na zginanie po zarysowaniu oblicza się ze średniej wytrzymałości na rozciąganie na zginanie po zarysowaniu f^f_cflm,Li zgodnie z [1] w następujący sposób.

Opis betonu zbrojonego włóknami stalowymi jest zatem przeprowadzany przez dodanie litery L oznaczającej klasę użytkowania z charakterystyczną wytrzymałością na rozciąganie na zginanie po zarysowaniu dla odkształceń 1 (SGU) i 2 (SGN). Na przykład beton zbrojony włóknami stalowymi C30/37 L0.9/L0.6 XC1 ma charakterystyczną wytrzymałość na rozciąganie na zginanie po zarysowaniu równą 0,9 N/mm² dla odkształcenia 1 i 0,6 N/mm² dla odkształcenia 2.

Krzywa naprężenie-odkształcenie betonu zbrojonego włóknami stalowymi

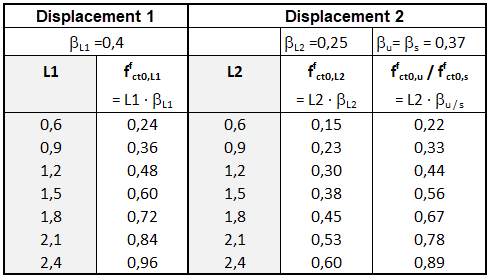
Krzywe naprężenie-odkształcenie są wymagane do wymiarowania stalowych elementów konstrukcyjnych. W tym celu, opisane powyżej charakterystyczne wytrzymałości na rozciąganie po zarysowaniu f^f_cflk,Li są konwertowane na wytrzymałości na rozciąganie osiowe po zarysowaniu f^f_ct0,i za pomocą współczynników β zgodnie z [1]. Tabela R3 wytycznych Niemieckiego Komitetu ds. Betonów Zbrojonych (DAfStb) w sprawie betonu zbrojonego włóknami stalowymi [1] przedstawia już podstawowe wartości wytrzymałości osiowej na rozciąganie po zarysowaniu f^{f f}_{ct0, i} dla odpowiednich klas wydajności (patrz Rysunek 05).

5 Gebräuchlichste Leistungsklassen L1 und L2 mit zugehörigen Grundwerten der zentrischen Nachrisszugfestigkeit

W celu uzyskania wartości obliczeniowych f^{f f}_{ctR, i} dla krzywej naprężenie-odkształcenie, należy zmodyfikować podstawowe wartości wytrzymałości na rozciąganie w kierunku osiowym po zarysowaniu o dwa współczynniki korekcyjne κ^f_G i κ^f_F .

Dyrektywa w sprawie włókien stalowych [1] zakłada, że odkształcenie 1 o = 0,5 mm w próbie 4-punktowego zginania odpowiada odkształceniu ε = 0,0035, a odkształcenie 2 o δ = 3,5 mm odpowiadają odkształceniu ε = 0.025.

W zależności od wprowadzonych obliczeń w [1] dla powierzchni rozciąganej dostępne są różne wykresy naprężenie-odkształcenie. W celu nieliniowego określenia odkształceń i sił wewnętrznych, w obszarze rozciągania zostaje zastosowana zależność multiliniowa pokazana na rysunku 06. Rozkład liniowy można stosować do momentu osiągnięcia wytrzymałości betonu na rozciąganie f_ctm. Zgodnie z [1] wykres naprężenie-odkształcenie oznaczony kolorem niebieskim na Rysunku 06 jest dozwolony tylko dla betonu zbrojonego włóknami stalowymi ze stosunkiem L2/L1 ≥ 0,7. W przypadku stosunków klas L2/L1 ≤ 0,7 można zastosować tylko rozkład naprężeń (zielona przerywana linia na Rysunku 06).

6 Spannungs-Dehnungs-Linie im Zugbereich nach [1] für die Schnittgrößen- und Verformungsermittlung bei nichtlinearen Verfahren

Zastosowanie wytrzymałości betonu na rozciąganie f_ctm nie jest dozwolone do wymiarowania przekroju w stanie granicznym nośności. Dodatkowa wytrzymałość na rozciąganie, którą można zastosować, wynika jedynie z siły rozciągającej przenoszonej przez włókna stalowe. Ponadto, dla obliczeń w stanie granicznym nośności należy zastosować wartości obliczeniowe f^f_ctd,Li. Uzyskuje się je poprzez pomnożenie obliczonych wartości f^f_ctR,Li przez współczynnik redukcji α^f_c i dzielenie przez częściowy współczynnik bezpieczeństwa γ^f_ct. Zastosowanie f^f_ctd,L1 und f^f_ctd,L2 (linia ciągła w kolorze niebieskim na Rysunku 7) jest ograniczone do stosunków L2/L1 ≥ 0,7. Rozkład naprężeń, pokazany na Rysunku 07 kolorem zielonym z myślnikami, może być stosowany w sposób uproszczony dla stosunków L2/L1 ≤ 1.

7 Spannungs-Dehnungs-Linie auf der Zugseite gemäß [1] für die Querschnittsbemessung im Grenzzustand der Tragfähigkeit

W strefie ściskania krzywej naprężenie-odkształcenie dla betonu zbrojonego włóknami stalowymi nie ma różnicy między zwykłym betonem bez włókien a betonem zbrojonym włóknami stalowymi. Przepis normy EN 1992-1-1 [4] stosuje się bez zmian do stosunku naprężenie-odkształcenie w obszarze ściskania. Z tego względu do nieliniowych obliczeń deformacji wewnętrznych i deformacji wewnętrznych zalecany jest wykres paraboliczny zgodnie z rozdz. 3.1.5 [4] (patrz siły ] dla zależności naprężenie-odkształcenie w obszarze ściskania.

8 Spannungs-Dehnungs-Linie nach [4] für den Druckbereich: a) für die nichtlineare Berechnung; b) für die Querschnittsbemessung

Obliczenia nieliniowe w RFEM

Zgodnie z [1], metody nieliniowe mogą być stosowane w przypadku elementów konstrukcyjnych z betonu zbrojonego włóknami stalowymi, jeżeli dominującą nośność uzyskuje się dzięki zastosowaniu stali zbrojeniowej. We wszystkich pozostałych przypadkach obliczenia nieliniowe można przeprowadzić tylko w przypadku elementów na podłożu sprężystym, zakotwionych płyt betonowych pod wodą, płyt stropowych wspartych na palach, powłokowych elementów konstrukcyjnych oraz monolitycznych elementów prefabrykowanych.

Poniżej przedstawiono krzywą naprężenie-odkształcenie w programie RFEM dla betonu zbrojonego włóknami stalowymi i sprawdzenie zachowania materiału. Na potrzeby tego artykułu będzie to początkowo przeprowadzane tylko dla elementu ES z jednokierunkowym rozciąganiem. Za pomocą tego prostego testu można zweryfikować model materiałowy zastosowany w programie RFEM pod kątem przejmowania jednoosiowego obciążenia rozciągającego.

W przypadku nieliniowych obliczeń sił wewnętrznych i odkształceń betonu zbrojonego włóknami stalowymi, wykres naprężenie-odkształcenie w obszarze ściskania składa się z paraboli zgodnie z 3.1.5 EN 1992-1-1 [4 ] oraz w obszarze rozciągania wieloliniowego rozkładu z uwzględnieniem wytrzymałości betonu na rozciąganie f_ctm (Rysunek 06). W programie RFEM należy użyć modelu materiałowego, który może reprezentować gałąź opadającą po powstaniu zarysowania. Dzięki modułowi dodatkowemu RF-MAT NL program RFEM może odwzorować dokładnie takie zachowanie na podstawie modelu materiałowego "Uszkodzenie izotropowe 2D/3D".

Model materiałowy „Uszkodzenie izotropowe” został szczegółowo opisany we wcześniejszym artykule:
KB 001461 │ Uszkodzenie nieliniowych modeli materiałowych

Krzywa naprężenie-odkształcenie jest zazwyczaj wprowadzana w programie RFEM. Powierzchnie ściskania i rozciągania można zdefiniować indywidualnie za pomocą opcji "Wykres ...". Tylko moduł sprężystości w początku musi być identyczny z odpowiednimi kolejnymi punktami w obszarach ściskania i rozciągania. Referencyjny rozmiar elementu l_{FE, R} pozostaje niezmieniony, a jego długość wynosi 0,0 m. Zapewnia to zastosowanie w obliczeniach zdefiniowanej krzywej naprężenie-odkształcenie w stosunku 1:1 w strefie uszkodzenia. Rysunek 09 przedstawia wprowadzanie analizy betonu zbrojonego włóknami stalowymi w oknie wprowadzania programu RFEM.

9 Definition der Spannungs-Dehnungs-Linie des Stahlfaserbetons

Ponieważ ilustracja przedstawiająca rozciąganie po zarysowaniu zostanie szczegółowo przeanalizowana poniżej, właściwości w obszarze rozciągania badanego betonu zbrojonego włóknami stalowymi są szczegółowo opisane poniżej:

• f_ctm = 2.500 N/mm²
• 1,04 ⋅ f^f_ctr,L1 = 0,862 N/mm²
• 1,04 ⋅ f^f_ctr,L2 = 0,458 N/mm²

Krzywa naprężenie-odkształcenie pokazana na rysunku 10 wynika z wyżej wymienionych parametrów materiałowych dla obszaru rozciąganego.

10 Model obliczeniowy w RFEM: ein FE-Element, links gehalten, rechts gezogen

Aby uniknąć wpływu sąsiednich elementów i stanów naprężeń dwuosiowych na wyniki, materiał jest sprawdzany na elemencie skończonym o długości boku 1 ⋅ 1 m. Element jest przytrzymywany poziomo po jednej stronie, a następnie ciągnięty po przeciwnej stronie. Aby uzyskać obraz wytrzymałości na rozciąganie po zarysowaniu, konieczne jest przyłożenie przemieszczenia w sposób kontrolowany czasowo, podobnie jak w opisanej powyżej 4-punktowej próbie zginania. Rysunek 11 przedstawia model obliczeniowy w programie RFEM.

11 Vorgabe der stufenweise ansteigenden Belastung

Korzystając z opcji "Stopniowe narastające obciążenie" w parametrach obliczeniowych przypadku obciążenia, odkształcenie jest zwiększane aż do osiągnięcia kryterium zerwania. Jako kryterium zerwania przyjęto przemieszczenie węzłowe wynoszące 25,1 mm, co odpowiada odkształceniu ε 0,0251.

12 Darstellung der 1. Membranspannung im Berechnungsdiagramm

Do oceny wyników obliczeń wykorzystuje się naprężenie membranowe w kierunku osi głównej σ_1,m. W oknie dialogowym 'Parametry obliczeń' można wyświetlić wykres wyników obliczeń dla przyrostu obciążenia, krok po kroku.

13 Gegenüberstellung der RFEM-Ergebnisse mit definierter Materialeigenschaft im Zugbereich

Obliczone naprężenie membranowe jest dokładnie zgodne z podanym rozkładem wytrzymałości na rozciąganie po zarysowaniu. Na poniższym wykresie naprężenie główne ma σ_1,m jest zdefiniowane przez krzywą naprężenie-odkształcenie betonu zbrojonego stalą, zdefiniowaną w obszarze rozciągania. Wyniki obliczone w programie RFEM dokładnie odpowiadają zdefiniowanej linii roboczej.

14 Spannungs-Dehnungs-Linie des Stahlfaserbetons im Zugbereich für eine nichtlineare Berechnung

Uwagi końcowe

Za pomocą modelu materiałowego „Uszkodzenie izotropowe 2D/3D” możliwe było dokładną weryfikację zachowania się betonu zbrojonego włóknami stalowymi w warunkach kontrolnych w przypadku jednoosiowego obciążenia rozciągającego. Należy pamiętać, że w przypadku takich obliczeń weryfikacyjnych, poprzez określenie referencyjnego rozmiaru elementu l_{FE, R,} wykluczone są wpływy np. sąsiednich elementów, wieloosiowych stanów naprężeń lub możliwości modyfikacji w modelu materiałowym.

Baza informacji

KB 001601 | Określanie właściwości materiałowych betonu zbrojonego włóknami stalowymi i ich zastosowanie w RFEM

Baza informacji

KB 001601 | Określanie właściwości materiałowych betonu zbrojonego włóknami stalowymi i ich zastosowanie w RFEM