Determinação das propriedades de material de betão reforçado com fibra de aço e a sua utilização no RFEM

Propriedades do material

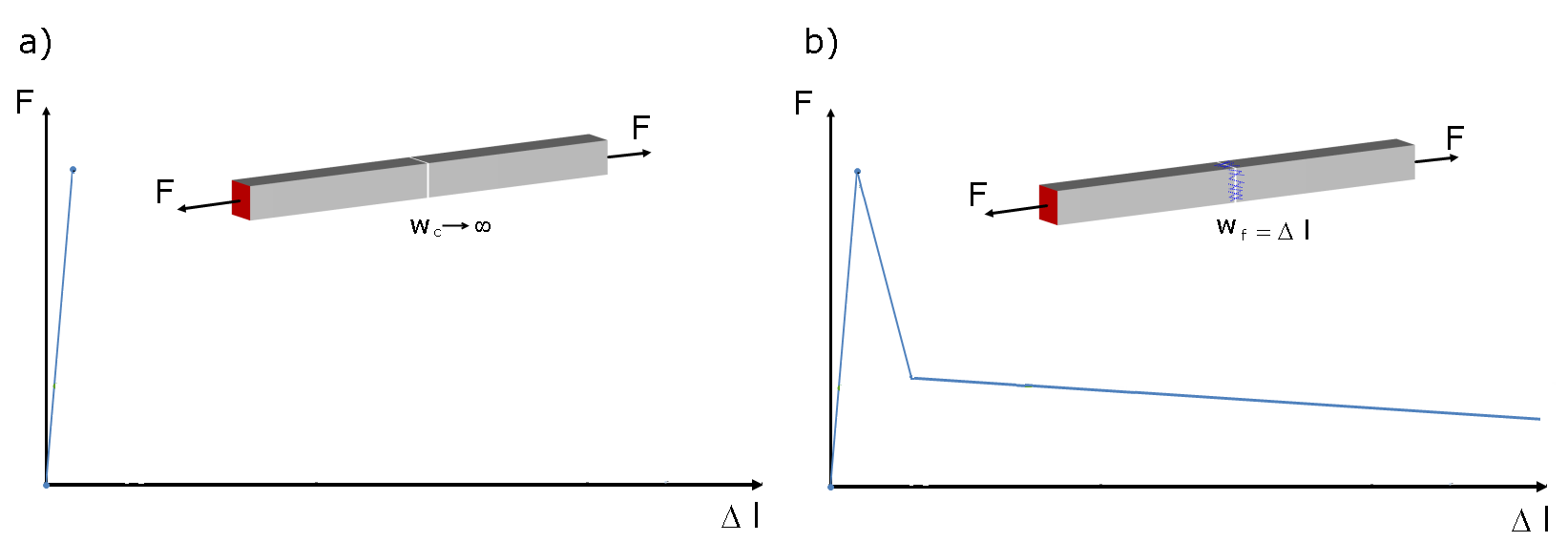
De acordo com a norma DIN EN 206-1, o betão armado com fibra é um betão ao qual a fibra de aço é adicionada para obter determinadas propriedades. Ao adicionar fibras de aço suficientes, elas podem transferir forças de tração através de uma fissura no betão. A Figura 01 compara o comportamento geral de betão não armado e o betão armado com fibra de aço sob tensão. O utilizador pode ver que a resistência à tração do betão armado com fibra de aço diminui com o aumento da deformação e a curva carga-deformação mostra um ramo descendente após ser atingida a resistência à tração.

Comportamento carga-deformação de a) betão sem armadura e b) Betão armado com fibra de aço

A resistência do material compósito betão armado com fibra de aço após exceder a resistência à tração do betão é denominada resistência à tração pós-fendilhação. As forças de tração que ocorrem realmente nas fibras de aço estão relacionadas com a superfície da zona de tração do betão. A tensão de tração pós-fendilhação é normalmente determinada através de um teste de tensão de flexão de acordo com [1] no laboratório de materiais de construção. Vigas com as dimensões b/h/l = 150 mm/150 mm/700 mm são utilizadas como amostras de teste. Uma vez que o comportamento à tração por flexão na zona de pós-fendilhação é importante para a linha de trabalho do betão armado com fibra de aço, o teste de flexão de 4 pontos é realizado de forma controlada do deslocamento. A Figura 02 mostra a representação gráfica dimensionada do teste de flexão de 4 pontos.

Prüfeinrichtung zur Ermittlung der Nachrissbiegezugfestigkeit (Abmessungen in mm)

Devido à configuração experimental do teste de flexão de 4 pontos, o local de fendilhação é arbitrário na viga de teste, porque a carga local entre os dois pontos de carga é constante. Na figura abaixo, pode ver a partir do teste final (a pressão foi estendida manualmente para aumentar a abertura da fenda após o final do teste) que a formação de fendas ocorre livremente entre os dois rolos de pressão na localização determinante (= posição mais fraca).

Ensaio de flexão de quatro pontos com abertura de fendas concluído (imagem: BPL Müller e Lobisch GmbH)

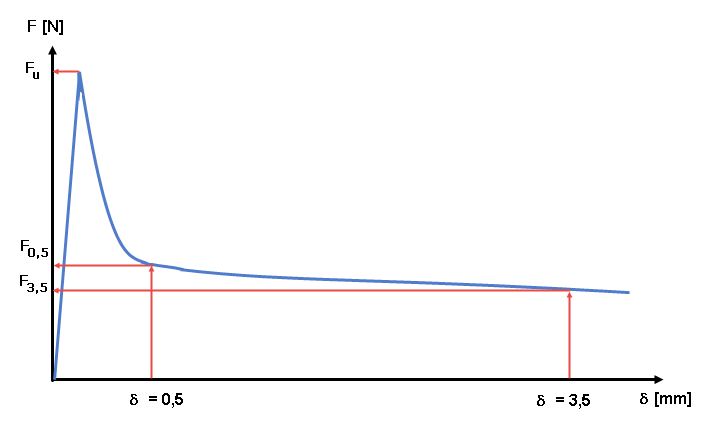
Os resultados do teste são documentados numa curva carga-deformação (ver Figura 04). A resistência à tração equivalente e, com a ajuda dos fatores de conversão, a resistência à tração pós-fendilhação do betão armado com fibra de aço são determinadas a partir desta curva carga-deformação. É estabelecida uma distinção entre um valor característico para a avaliação do estado limite de utilização (= pequenas deformações, δ = 0,5 mm) e um parâmetro determinante para o estado último (= deformações grandes, δ = 3,5 mm).

Curva carga-deformação simbólica para determinação das resistências à tração pós-fendilhação

A resistência à tração por flexão após fendilhação do betão armado com fibra de aço é determinada a partir dos valores de carga F_0,5 para δ = 0,5 mm e F_3,5 para δ = 3,5 mm. Neste caso, é atingida a carga L_i (com i = 0.5 e respectivamente 3.5) é multiplicada pela carga do braço de alavanca relacionada e dividida por esse módulo de secção W_j da secção não fendilhada. A média da resistência à tração por flexão pós-fendilhação f^f_cflm,Li de uma série de n vigas de teste é obtida como média aritmética das resistências à tração pós-fendilhação.

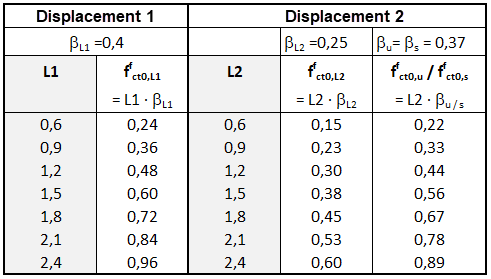
Para a classificação do material compósito de betão armado com fibra de aço, a Diretiva do Comité Alemão para o betão armado com fibra de aço de aço de aço (DAfStb) especifica duas classes de desempenho diferentes: L1 e L2. A classe de desempenho L1 descreve as propriedades do material para pequenas deformações (δ = 0,5 mm) e a classe de desempenho L2 o comportamento para deformações maiores (δ = 3,5 mm). A descrição das classes de desempenho Li corresponde ao valor característico da resistência à tração final por fadiga f^f_cflk,Li em N/mm² para as correspondentes deformações. De acordo com [1] a resistência à tração por flexão característica é calculada a partir da resistência à tração elástica média máxima f^f_cflm,Li.

Onde
Lf^f_cflm,Li ... valor médio dos resultados de um único teste logaritimizado f^f_cfl,Li,j (para detalhes ver [1])
L_s ... desvio padrão dos resultados do teste individuais logaritmizados (para mais detalhes, ver [1]
k_s ... fator de correção da porção para desvios padrão desconhecidos para a porção de 5% com um nível de confiança de 75% (ver detalhes [1])

Assim, a descrição do betão armado com fibra de aço é realizada adicionando a letra L para a classe de desempenho com a resistência à tracção à flexão característica para as deformações 1 (SLS) e 2 (ULS). Por exemplo, um betão armado com fibras de aço C30/37 L0,9/L0,6 XC1 apresenta uma resistência à tracção devido à flexão de 0,9 N/mm² para a deformação 1 e 0,6 N/mm² para a deformação 2.

Curva tensão-deformação de betão armado com fibra de aço

Os diagramas de tensão-deformação são necessários para o dimensionamento de componentes de aço estrutural. Para este efeito, as resistências à tração por flexão características f^f_cflk,Li descritas acima, são convertidas nas resistências à tracção axial f^f_ct0,i através de fatores β de acordo com [1]. As linhas de orientação na tabela R3 da Agência Alemã para o betão armado (DAfStb) sobre o betão armado com fibra de aço ;[1] apresentam já os valores base para a resistência à tração axial pós fendilhação f^f_ct0,i para a respetiva classe de desempenho (ver Figura 05).

Gebräuchlichste Leistungsklassen L1 und L2 mit zugehörigen Grundwerten der zentrischen Nachrisszugfestigkeit

De modo a obter os valores de cálculo f^f_{ctR, i} para a curva de tensão-deformação, tem de se modificar os valores base da resistência à tração axial por dois fatores de correção κ^f_G e κ^f_F.

f^f_ctR,i = κ^f_G ⋅ κ^f_F ⋅ f^f_ct0,i

Onde
κ^f_G ... fator para considerar a influência do tamanho do componente estrutural no coeficiente de variação = 1,0 + A^f_ct ⋅ 0,5 <1,70
A_ct ... área da secção transversal sujeita a tensões de tração das áreas fendilhadas em m² pertencente ao respectivo estado de equilíbrio
κ^f_F ... fator para considerar a orientação da fibra = 0,5. Para os componentes estruturais planos, horizontais (b <5), é permitido assumir κ^f_F = 1,0 para tensões de flexão e tração.

A Diretiva das Fibras de Aço [1] assume que a deformação 1 com δ = 0,5 mm do teste de flexão de 4 pontos com uma deformação de ε = 0,0035 e a deformação 2 com δ = 3,5 mm corresponde a uma deformação de ε = 0,025.

Dependendo do cálculo fornecido, encontram-se disponíveis diferentes diagramas de tensão-deformação em [1] para a área de sujeita a tração. Para uma determinação não linear da deformação e das forças internas, a relação multilinear apresentada na Figura 06 é aplicada na área de tração. A distribuição linear pode ser aplicada até ser atingida a resistência à tração do betão f_ctm. De acordo com [1] , a curva tensão-deformação apresentada em azul na Figura 06 é permitida apenas para betão armado com fibras de aço com uma relação L2/L1 ≥ 0,7. Para relações da classe de desempenho L2/L1 ≤ 0,7, apenas é permitido aplicar o bloco de tensões (linha pontilhada a verde na Figura 06).

Spannungs-Dehnungs-Linie im Zugbereich nach [1] für die Schnittgrößen- und Verformungsermittlung bei nichtlinearen Verfahren

Para o dimensionamento da secção ao estado limite último, a resistência à tração do betão f_ctm não pode ser aplicada. A resistência à tração adicional que pode ser aplicada provém apenas da força de tração transmitida na fenda através das fibras de aço. Além disso, tem de ser aplicada a resistência à tração para a verificação do estado limite último com os valores de cálculo f^f_ctd,Li . Estes são obtidos através da multiplicação dos valores calculados de f^f_ctR,Li pelo coeficiente de redução α^f_c e pela divisão pelo coeficiente de segurança parcial γ^f_ct . A aplicação de f^f_{ctd, L1} e f^f_{ctd, L2} (linha sólida azul na Figura 7) é restrita à relações de L2/L1 ≥ 0,7. A distribuição de tensões, representada a verde com traços na Figura 07, pode ser utilizada de forma simplificada para as relações L2/L1 ≤ 1.

Spannungs-Dehnungs-Linie auf der Zugseite gemäß [1] für die Querschnittsbemessung im Grenzzustand der Tragfähigkeit

Na zona de compressão da curva tensão-deformação para o betão armado com fibras de aço, não existe diferença entre o betão normal sem fibras e o betão armado com fibras de aço. A regulação de EN 1992-1-1 [4] aplica-se inalterada à relação tensão-deformação na área de compressão. Portanto, um diagrama em parábola de acordo com o Capítulo 3.1.5 [4] (ver Figura 08 a) ou uma parábola retangular de acordo com o Capitulo 3.1.6 [4] para curva tensão-deformação é utilizada para o cálculo não linear da fricção e das forças internas a serem utilizadas na área de compressão.

Spannungs-Dehnungs-Linie nach [4] für den Druckbereich: a) für die nichtlineare Berechnung; b) für die Querschnittsbemessung

Cálculo não linear com o RFEM

De acordo com [1], os métodos não-lineares podem, em princípio, ser utilizados para os componentes estruturais de betão armado com fibra de aço se a capacidade resistente predominante é alcançada pela armadura de aço. Em todos os outros casos, o cálculo não linear é aplicável apenas para os componentes estruturais com fundações elásticas, lajes de betão ancoradas submersas, lajes de piso apoiadas por estacas, componentes estruturais em forma de casca e cascos monoliticos pré-fabricados.

No texto seguinte, a curva tensão-deformação para o betão armado com fibra de aço será definida no RFEM e será verificado o comportamento do material. Para efeitos do presente artigo, inicialmente apenas será realizado num elemento EF com uma carga de tração uniaxial. Através deste ensaio simples, o modelo de material utilizado no RFEM será verificado para a absorção de uma carga de tração uniaxial.

Para um cálculo não linear das forças internas e deformações do betão armado com fibras de aço, a curva tensão-deformação aplicada na área de compressão consiste numa parábola de acordo com 3.1.5 EN 1992-1-1 [4] e na área de tração da distribuição multilinear tendo em consideração a resistência à tração do betão f_ctm (Figura 06). No RFEM, tem de ser utilizado um modelo de material que pode representar o ramo descendente após a formação de fendas. Com o módulo adicional RF-MAT NL, o RFEM pode representar exatamente este comportamento com o modelo de material "Dano isotrópico 2D/3D". Num artigo anterior, já foi descrito em detalhe o modelo de material "Dano isotrópico". Geralmente, a curva tensão-deformação é introduzida no RFEM. As zonas de compressão e tração podem ser definidas individualmente através da opção "Diagrama". Apenas o módulo de elasticidade na origem tem de ser idêntico aos respetivos pontos sucessores nas zonas de compressão e tração. O tamanho do elemento de referência l_FE,R permanece inalterado com um comprimento de 0,0 m. Assim, é garantido que a curva de tensão-deformação definida é aplicada 1:1 na zona de avaria no cálculo. A Figura 09 mostra a entrada do betão armado com fibra de aço analisado na janela de entrada do RFEM.

Definition der Spannungs-Dehnungs-Linie des Stahlfaserbetons

Uma vez que a ilustração do comportamento da tracção pós fendilhação deve ser analisada em detalhe abaixo, as propriedades na área de tração do betão armado com fibra de aço testadas são descritas em detalhe abaixo:

f_ctm = 2,500 N/mm²
1,04 ⋅ f^f_ctr,L1 = 0,862 N/mm²
1,04 ⋅ f^f_ctr,L2 = 0,458 N/mm²

A curva tensão-deformação apresentada na Figura 10 resulta das propriedades de material anteriormente mencionadas para a área de tração.

Modelo de cálculo no RFEM: ein FE-Element, links gehalten, rechts gezogen

De forma a evitar a influência dos elementos vizinhos e dos estados de tensão biaxiais nos resultados, o material é verificado num elemento finito com comprimentos laterais de 1 ⋅ 1 m. O elemento é fixo horizontalmente num lado do elemento e depois puxado no lado oposto. Para obter a imagem da resistência à tração após fendilhação, é necessário aplicar o deslocamento de uma forma controlada no tempo, como no teste de flexão de 4 pontos acima descrito. A Figura 11 apresenta o modelo de cálculo no RFEM.

Vorgabe der stufenweise ansteigenden Belastung

Utilizando a opção "Carregamento crescente gradual" nos parâmetros de cálculo do caso de carga, a deformação é aumentada até ser atingido o critério de ruptura. O critério de rotura utilizado foi definido com um deslocamento nodal de 25,1 mm, o que corresponde a uma deformação ε de 0,0251.

Darstellung der 1. Membranspannung im Berechnungsdiagramm

Para avaliar os resultados do cálculo, é utilizado o diafragma de tensões na direção do eixo principal σ_1,m. Na caixa de diálogo "Parâmetros de cálculo", pode exibir um diagrama para os resultados do cálculo para um aumento de carga passo a passo.

Gegenüberstellung der RFEM-Ergebnisse mit definierter Materialeigenschaft im Zugbereich

A tensão da membrana calculada segue exatamente a distribuição especificada da resistência à tração pós-fendilhação. No diagrama seguinte, a tensão principal σ_1,m is definida pela curva de tensão-deformação do betão armado com fibra de aço definido na área de tração. Os resultados calculados no RFEM correspondem precisamente à linha de trabalho definida.

Spannungs-Dehnungs-Linie des Stahlfaserbetons im Zugbereich für eine nichtlineare Berechnung

Resumo

Utilizando o modelo de material "Dano isotrópico 2D/3D", foi possível verificar com precisão o comportamento de verificação do betão armado com fibra de aço no caso de carregamento de tração uniaxial. Tenha em atenção que para tais cálculos de verificação, todas as influências a partir de, por exemplo, elementos vizinhos, estados de tensão de eixos múltiplos ou opções de modificação no modelo de material são excluídas através da especificação de um tamanho de elemento de referência l_FE,R.