Przerwanie obliczeń z powodu niestabilnego systemu może mieć różne przyczyny. Z jednej strony może wskazywać na „rzeczywistą” niestabilność z powodu przeciążenia systemu, z drugiej strony mogą być za nią odpowiedzialne błędy modelowania. Poniżej przedstawiono możliwy sposób postępowania, aby zidentyfikować przyczynę niestabilności.
1. Kontrola modelowania
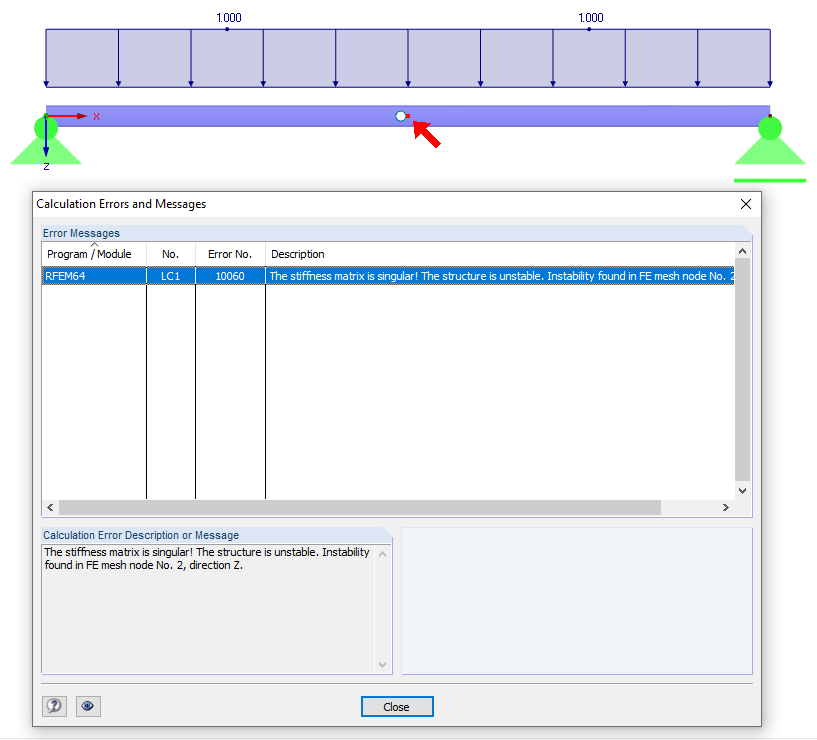
Na początku należy sprawdzić, czy system jest poprawnie zamodelowany. W tym celu warto skorzystać z kontroli modelu dostępnych w programach RFEM 5 / RSTAB 8 (Extras → Kontrola modelu). Za pomocą tych narzędzi można na przykład znaleźć i usunąć identyczne węzły i nałożone pręty.
Dodatkowo można obliczyć strukturę np. pod wpływem ciężaru własnego w przypadku obciążenia według teorii pierwszego rzędu. Jeśli w tym przypadku wyniki są dostępne, struktura jest stabilna pod względem modelowania. Jeśli nie, poniżej przedstawiono najczęstsze przyczyny (zob. także wideo "Kontrola modelu" w sekcji "Pobieranie"):
Niepoprawna definicja podpór / Brak podpór
Może to prowadzić do niestabilności, ponieważ system nie jest utrzymywany we wszystkich kierunkach. Dlatego wymagane jest, aby warunki podparcia były w równowadze z systemem oraz z zewnętrznymi warunkami granicznymi. Systemy statycznie niewyznaczalne również mogą prowadzić do przerwania obliczeń z powodu niedostatecznych warunków granicznych.
Skręcanie prętów wokół własnej osi
Gdy pręty skręcają się wokół własnej osi, tzn. pręt nie jest utrzymywany wokół własnej osi, może to prowadzić do niestabilności. Często przyczyną są ustawienia przegubów końcowych prętów. Może się zdarzyć, że zarówno na początku, jak i na końcu są wprowadzone przeguby skrętne. Wówczas przy oknie ostrzeżenia podczas rozpoczynania obliczeń program zwróci uwagę użytkownika.
Brak połączenia prętów
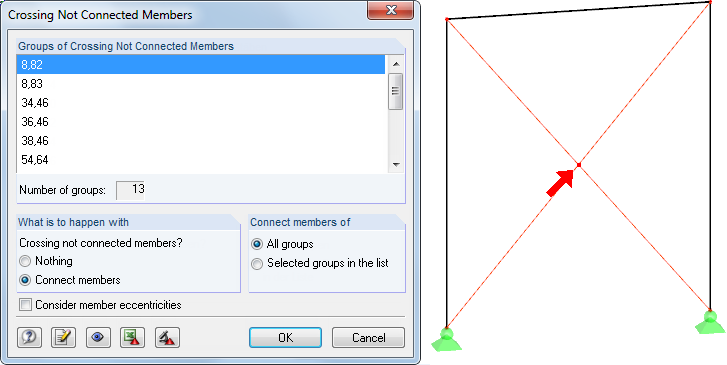
Zwłaszcza w większych i bardziej złożonych modelach łatwo jest, aby kilka prętów nie było ze sobą połączonych, przez co "unoszą się w powietrzu". Zapomnienie o krzyżujących się prętach, które powinny się przecinać, również może prowadzić do niestabilności. Rozwiązanie oferuje kontrola modelu „Kreuzende, nicht verbundene Stäbe”, która wyszukuje pręty, które się krzyżują, ale nie mają wspólnych węzłów w punkcie przecięcia.
Brak wspólnego węzła
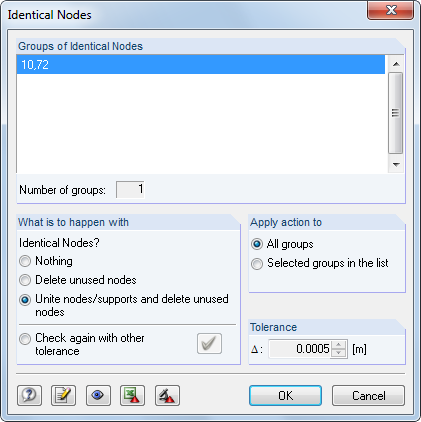
Węzły wydają się znajdować w tym samym miejscu, ale przy bliższej analizie są minimalnie od siebie oddalone. Częstymi przyczynami są importy CAD, które można jednak oczyścić za pomocą kontroli modelu.
Powstawanie łańcucha przegubowego
Zbyt wiele przegubów prętowych w jednym węźle może powodować powstanie łańcucha przegubowego, prowadzącego do przerwania obliczeń. Na każdy węzeł można zdefiniować tylko n-1 przeguby o tych samych stopniach swobody w odniesieniu do globalnego układu współrzędnych, gdzie „n” oznacza liczbę podłączonych prętów. To samo dotyczy przegubów liniowych.
2. Kontrola usztywnienia
Brak usztywnienia również prowadzi do przerwań obliczeń w wyniku niestabilności. Dlatego należy zawsze sprawdzić, czy struktura jest wystarczająco usztywniona we wszystkich kierunkach.
3. Problemy numeryczne
Do tego punktu w obrazie 08 pokazano przykład. Jest to rama przegubowa usztywniona przez pręty napinające. Z powodu skracania słupków pod wpływem obciążeń pionowych pręty napinające w pierwszym przebiegu obliczeń uzyskują małe siły ściskające. Są one usuwane z systemu (ponieważ mogą przyjmować tylko naprężenia). W drugim przebiegu obliczeń, model bez tych prętów napinających jest wówczas niestabilny. Istnieją różne możliwości rozwiązania tego problemu. Możesz przypisać naprężenie wstępne (obciążenie prętowe) do prętów napinających, aby „wyeliminować” małe siły ściskające, przypisać prętom małą sztywność lub pozwolić na usunięcie prętów jeden po drugim w obliczeniach (zob. obraz 08).
4. Identyfikacja przyczyny niestabilności
Automatyczna kontrola modelu z graficznym wyjściem
Aby uzyskać graficzne przedstawienie przyczyny niestabilności, moduł RF-STABIL (dla RFEM 5) lub dodatek Stabilność strukturalna (dla RFEM 6) może być pomocny. Za pomocą opcji „Określ formę własną niestabilnego modelu” (zob. obraz 09) lub „Oblicz bez obciążenia dla dowodu niestabilności przez formę własną” można obliczyć potencjalnie niestabilne systemy. Na podstawie danych strukturalnych prowadzona jest analiza wartości własnych, tak że jako wynik niestabilność danego elementu jest graficznie przedstawiona.
Problem bifurkacji
Jeśli przypadki obciążeń lub kombinacje obciążeń można obliczyć według teorii I rzędu i obliczenia przerwane są dopiero od teorii II rzędu, to mamy do czynienia z problemem stabilności (czynnik obciążenia bifurkacyjnego mniejszy od 1,00). Czynnik obciążenia bifurkacyjnego określa, o ile razy należy pomnożyć obciążenie, aby model pod danym obciążeniem stał się niestabilny (np. wywracał się). Z tego wynika: Czynnik obciążenia bifurkacyjnego mniejszy niż 1,00 oznacza, że system jest niestabilny. Tylko pozytywny czynnik obciążenia bifurkacyjnego powyżej 1,00 pozwala stwierdzić, że obciążenie pomnożone przez ten czynnik prowadzi do wywrotki stabilnego systemu. Aby znaleźć „słabe ogniwo”, zaleca się następujące postępowanie, które wymaga modułu RSKNICK (RSTAB 8) lub RF-STABIL (RFEM 5) lub dodatku Stabilność strukturalna (RFEM 6 / RSTAB 9) (zob. także wideo „Problem bifurkacji” w sekcji „Pobieranie”).
Najpierw należy zmniejszyć obciążenie danej kombinacji obciążeń aż do momentu, gdy kombinacja obciążeń stanie się stabilna. Pomocny tutaj jest czynnik obciążenia w parametrach obliczeń kombinacji obciążeń. Odpowiada to również ręcznemu określeniu czynnika obciążenia bifurkacyjnego, jeśli powyższe moduły lub dodatki nie są dostępne. W przypadku czysto liniowych elementów konstrukcyjnych może być wystarczające, aby obliczyć kombinację obciążeń według teorii I rzędu i obliczyć ją bezpośrednio w module dodatkowym lub pozwolić na określenie obciążenia bifurkacyjnego za pomocą dodatku. Na podstawie graficznej figury wyboczenia lub ugięcia tej kombinacji obciążeń można zidentyfikować „słabe ogniwo” w systemie i podjąć działania zaradcze. Aby oprócz globalnych form własnych uwzględnić również lokalne formy zniszczenia prętów, w module RF-STABIL (RFEM 5) należy włączyć podział prętów lub w module RSKNICK (RSTAB 8) ustawić podział prętów kratowych na co najmniej „2”. Dla dodatku Stabilność strukturalna (RFEM 6 / RSTAB 9) należy sprawdzić, czy aktywowano podziały dla prętów.
Zobacz linki w tej FAQ.