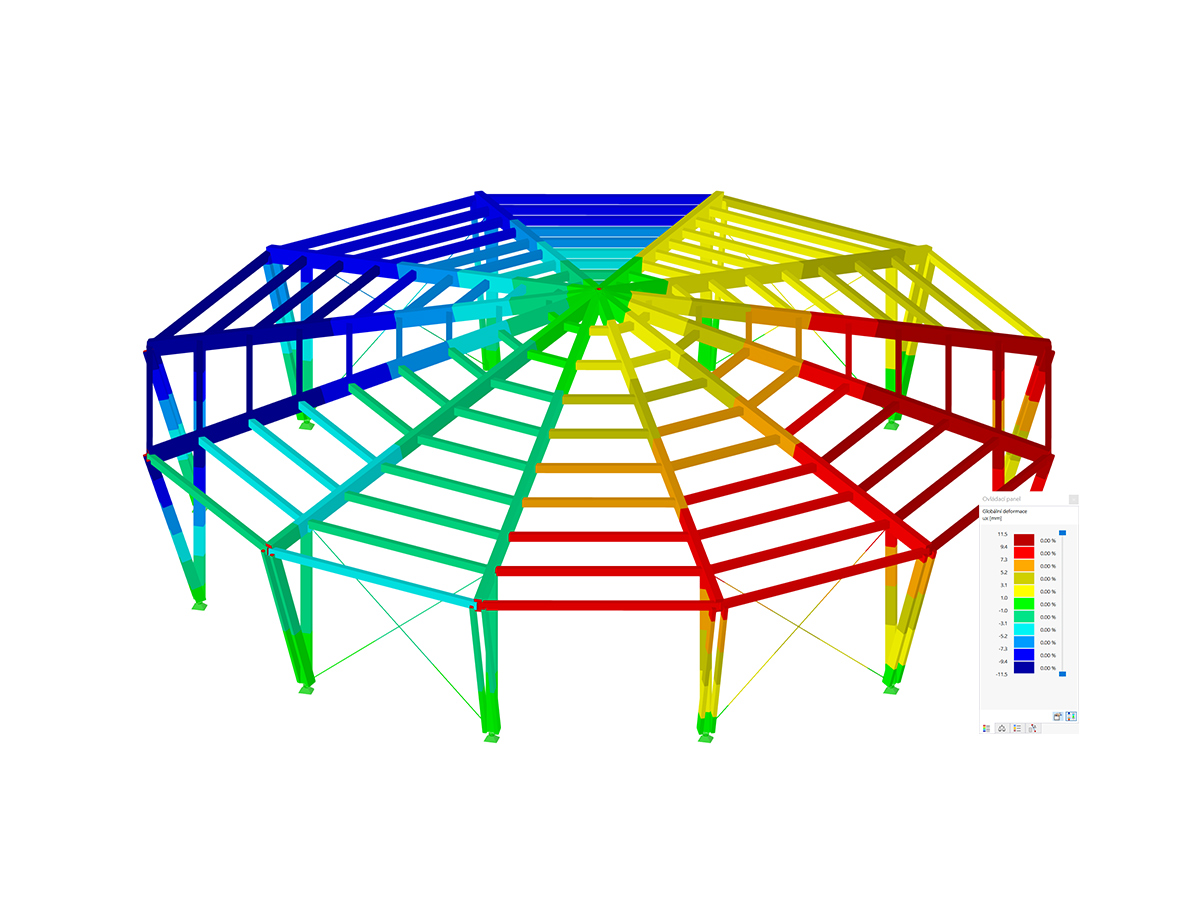
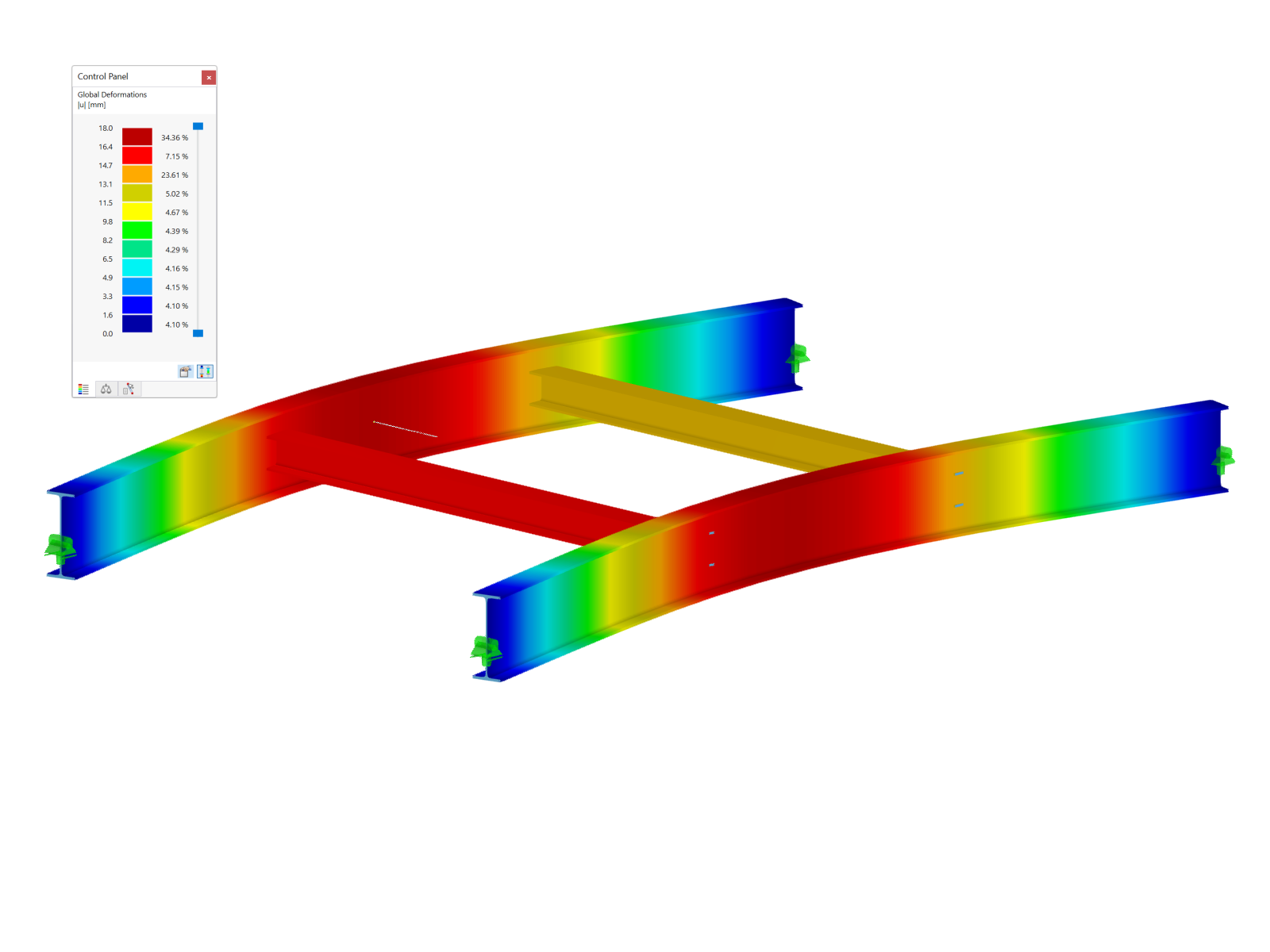
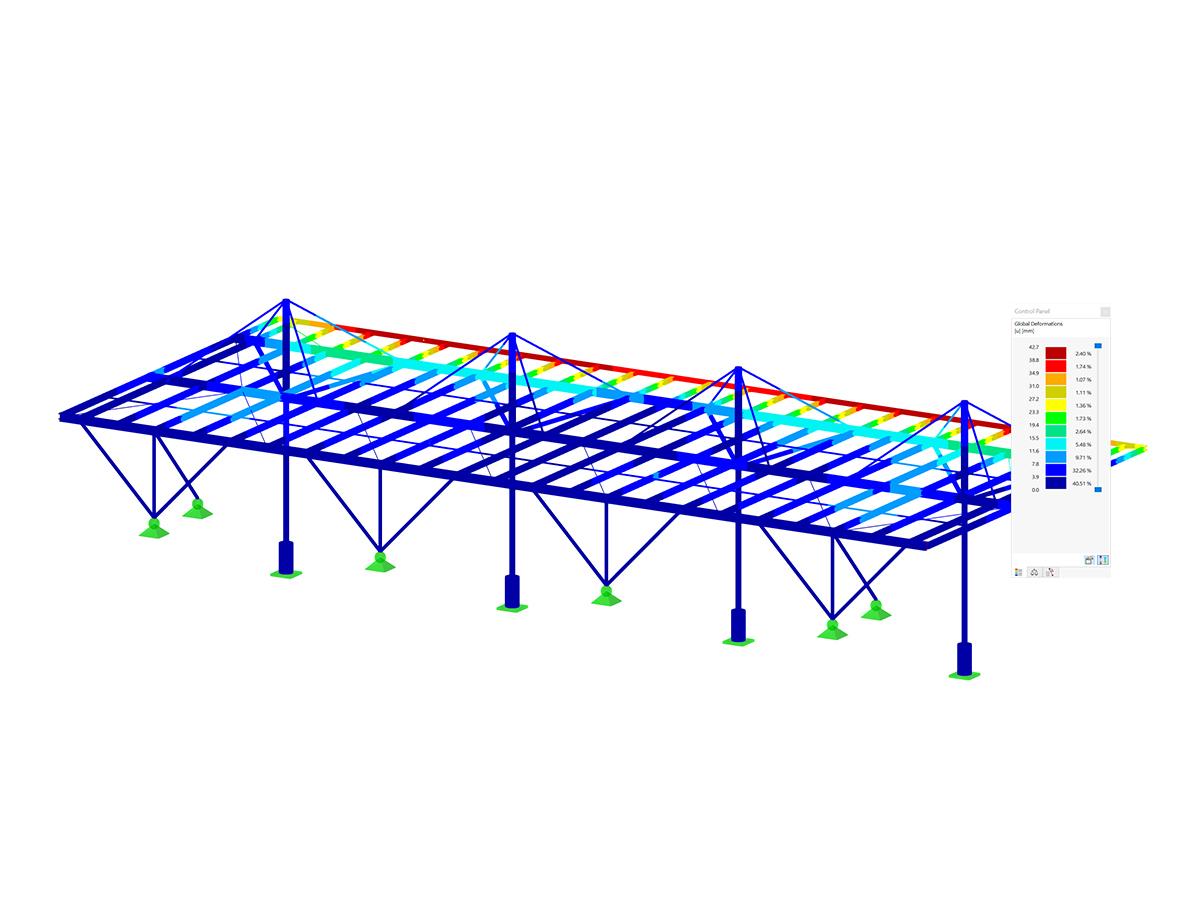
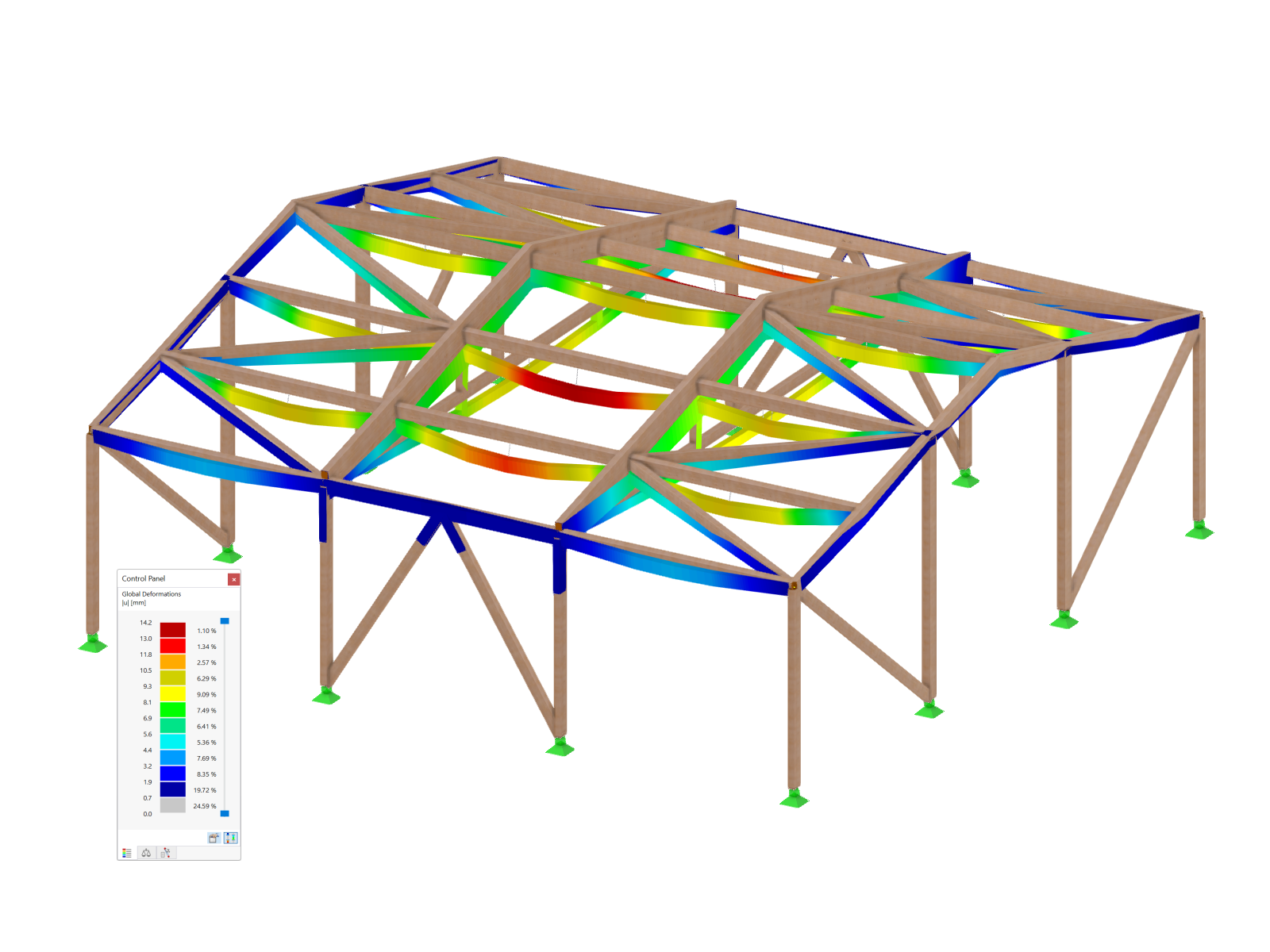
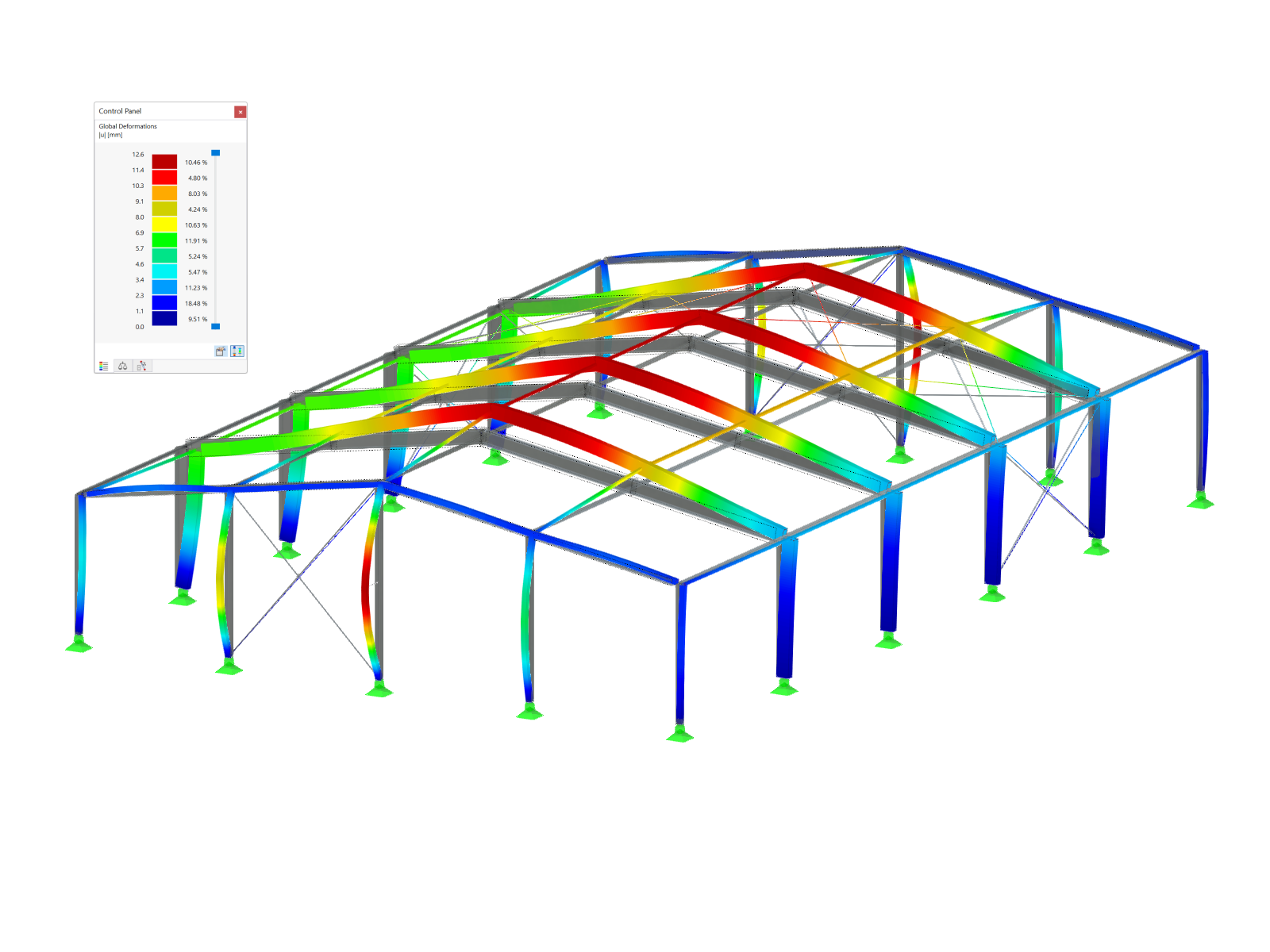
The critical load factor indicates the number by which the load must be multiplied until the model under the associated load becomes unstable (buckling).
The critical load factor is determined internally by a load increment. The obtained load factor becomes the critical load factor when the program can no longer find the equilibrium in the deformed system for the given loading condition (= becomes unstable).
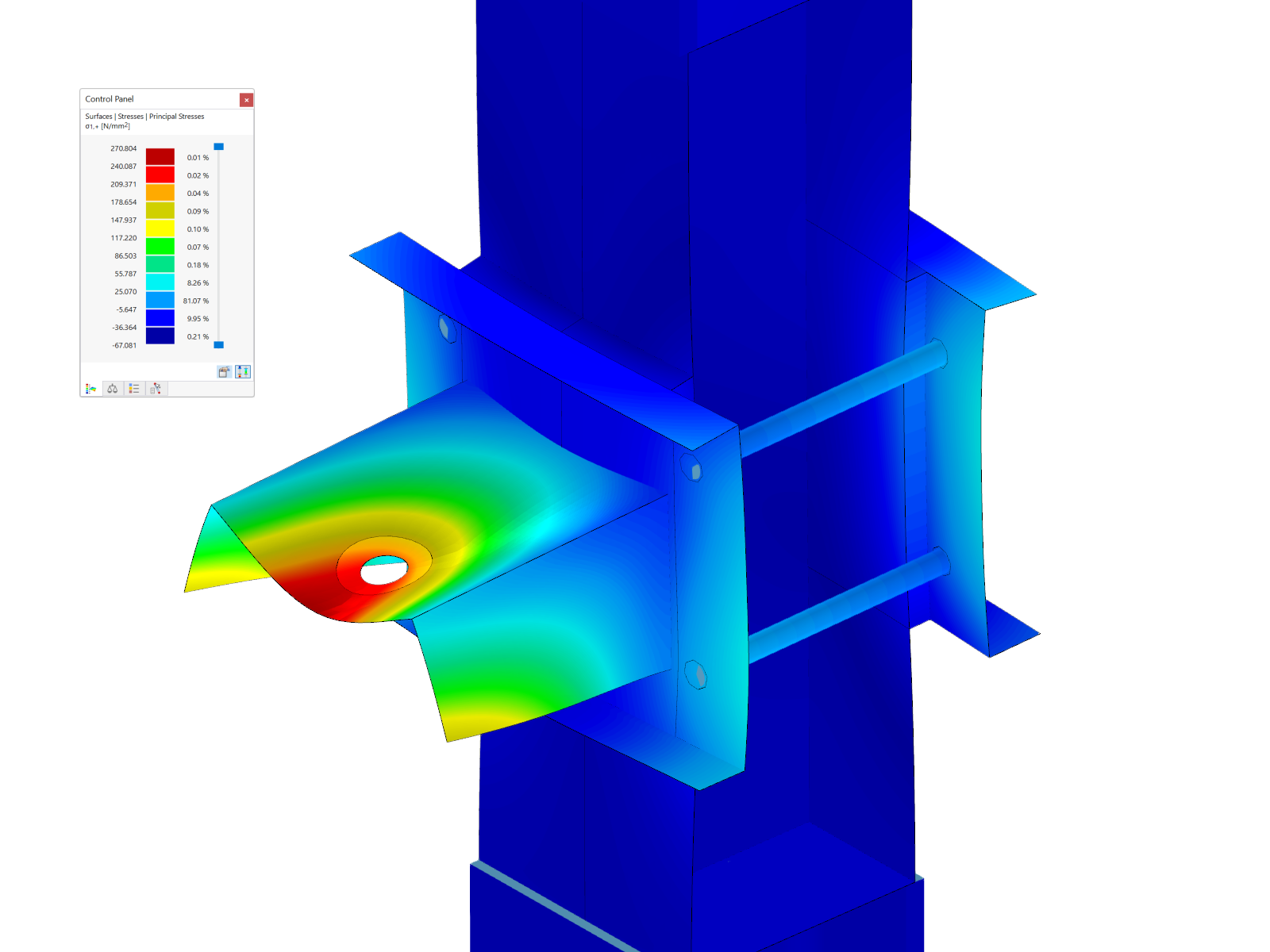
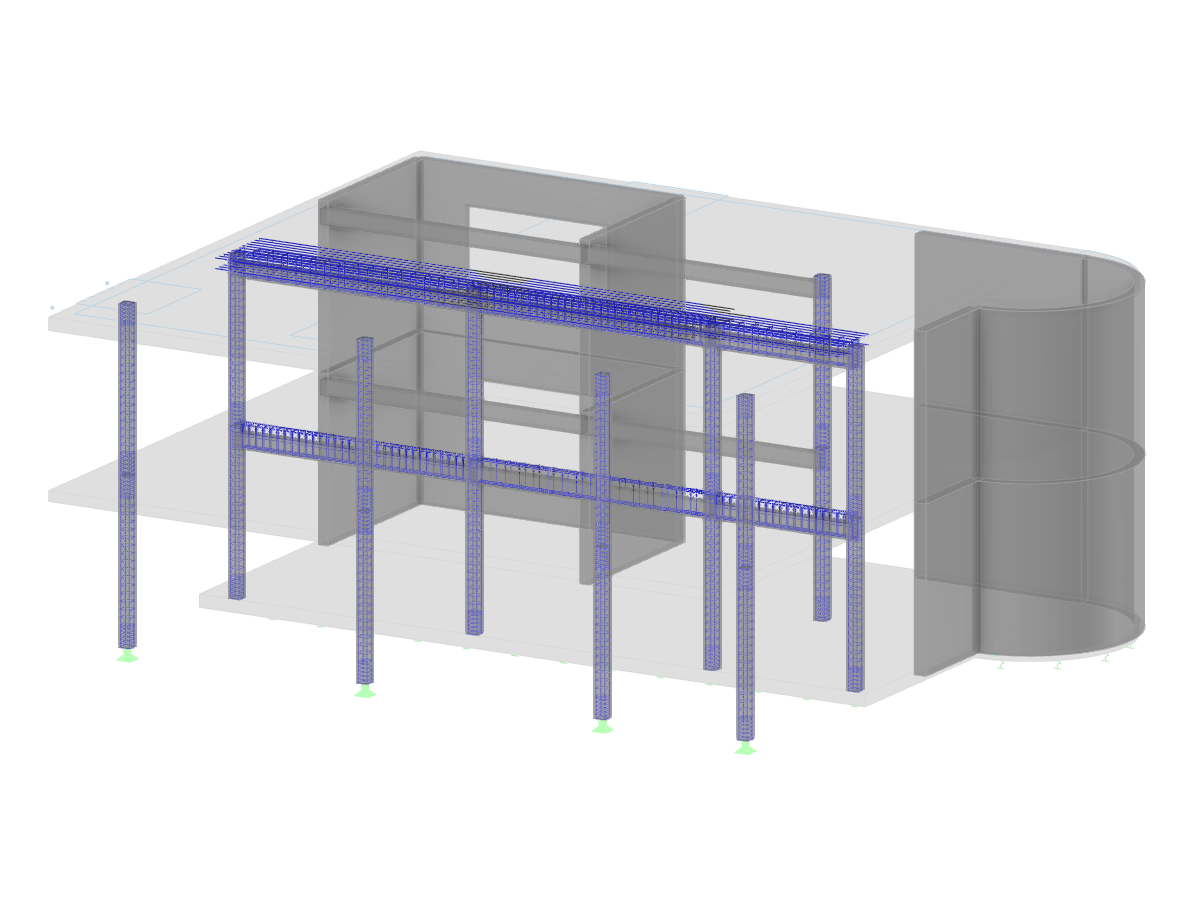
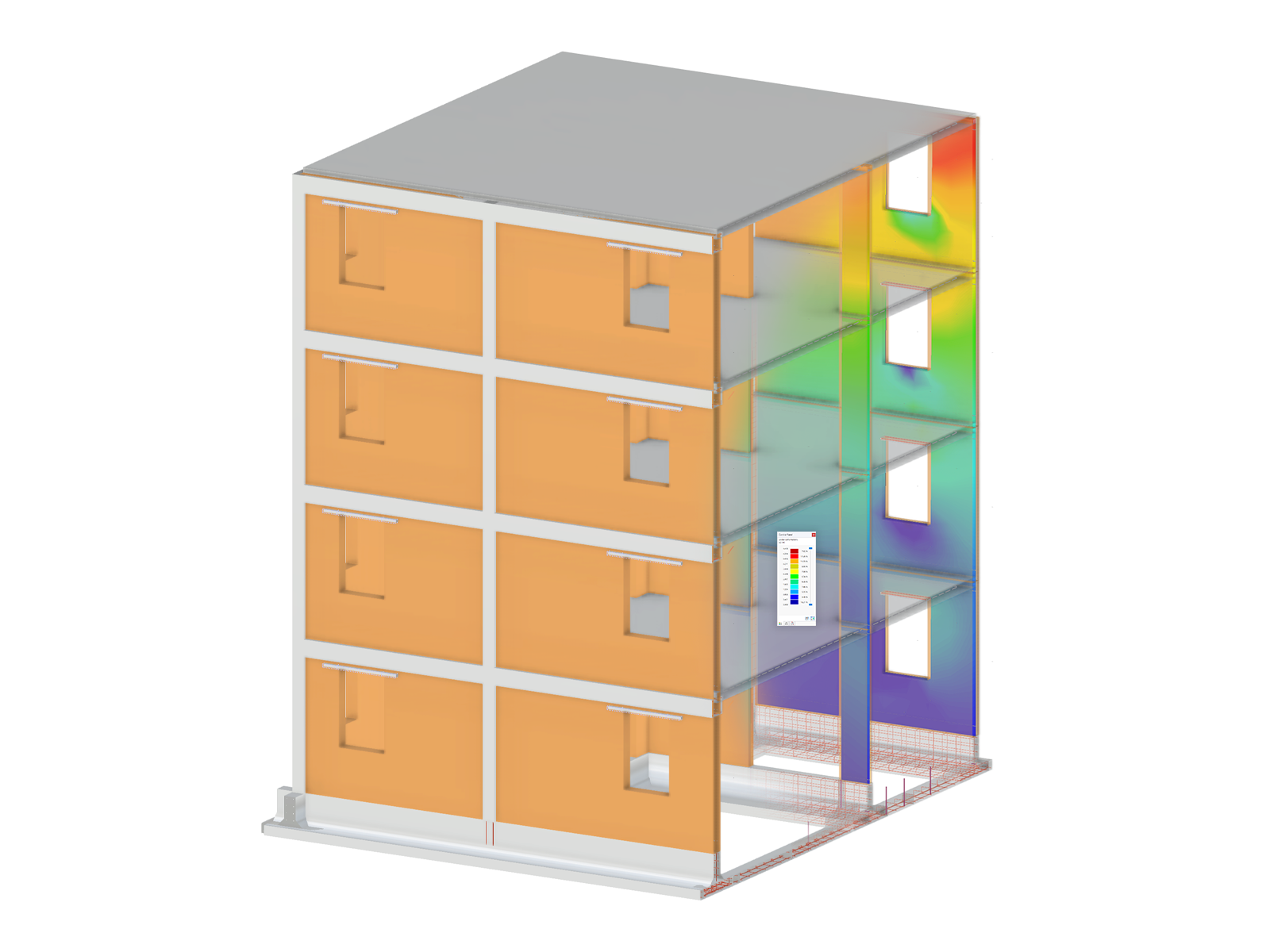
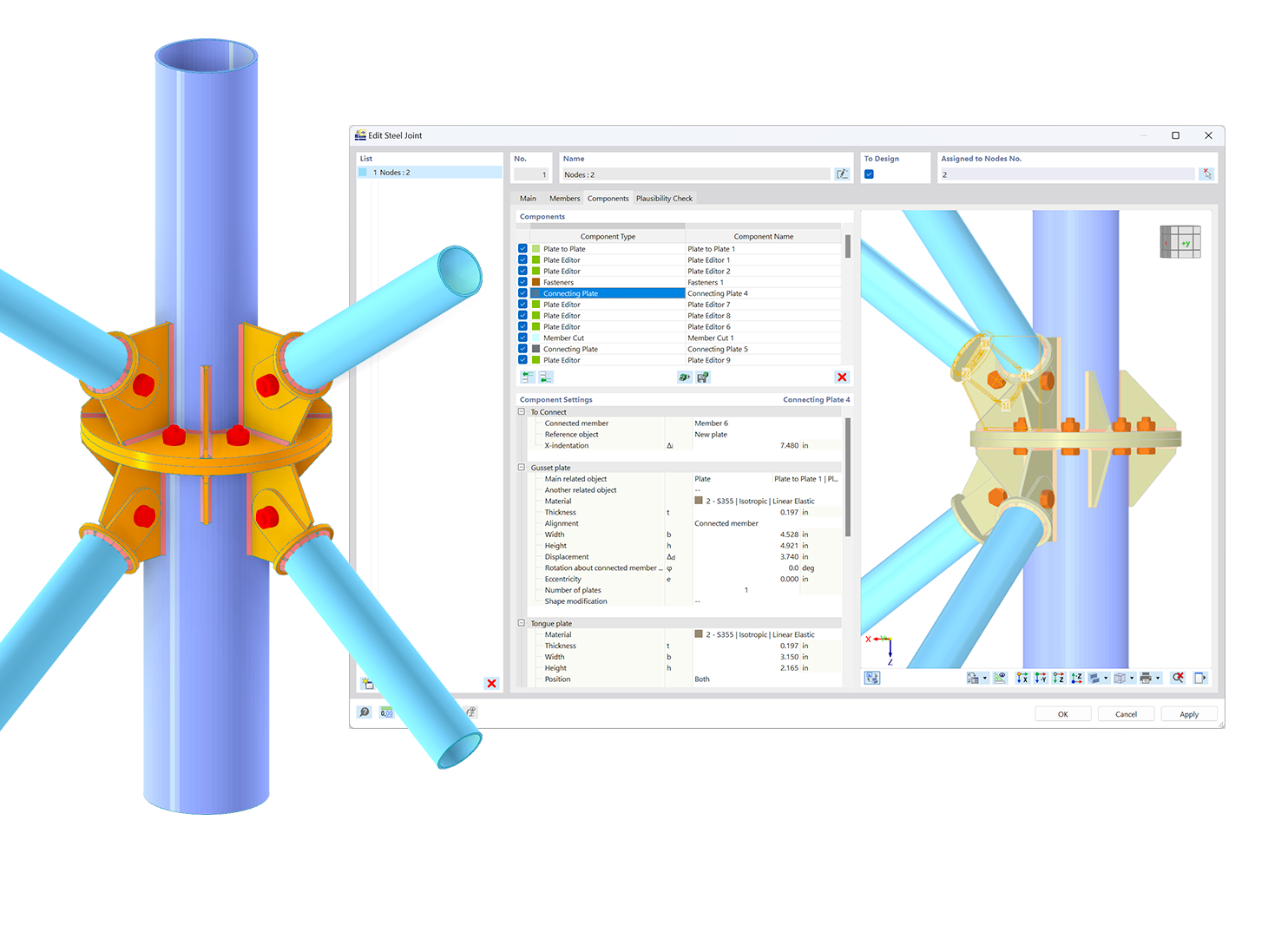
In contrast to the solution of a buckling eigenvalue problem (such as in RS-BUCK and RF-STABILITY), this procedure also helps you consider other structural nonlinearities (for example, support failures, member failures, and so on) in an optimal way.
You can activate the calculation of the critical load factor for each load case and load combination in the "Calculation Parameters" tab. For the iterative process itself, an initial load factor k0 and a load factor increment Δk must be specified. In addition, you can define the process more precisely by specifying a refinement, an additional stopping condition, and an initial load.
If the program can no longer find the equilibrium for load factor 1.0, and the initial load factor is < 1.0 (unstable), no result is given due to the lack of internal forces and deformations in load step 1.0.
Since the calculation of the critical load factor can significantly increase the computation time due to the iterative approach, you should set this function only for the desired load situations (LC, CO).













































_1.jpg?mw=350&hash=ab2086621f4e50c8c8fb8f3c211a22bc246e0552)






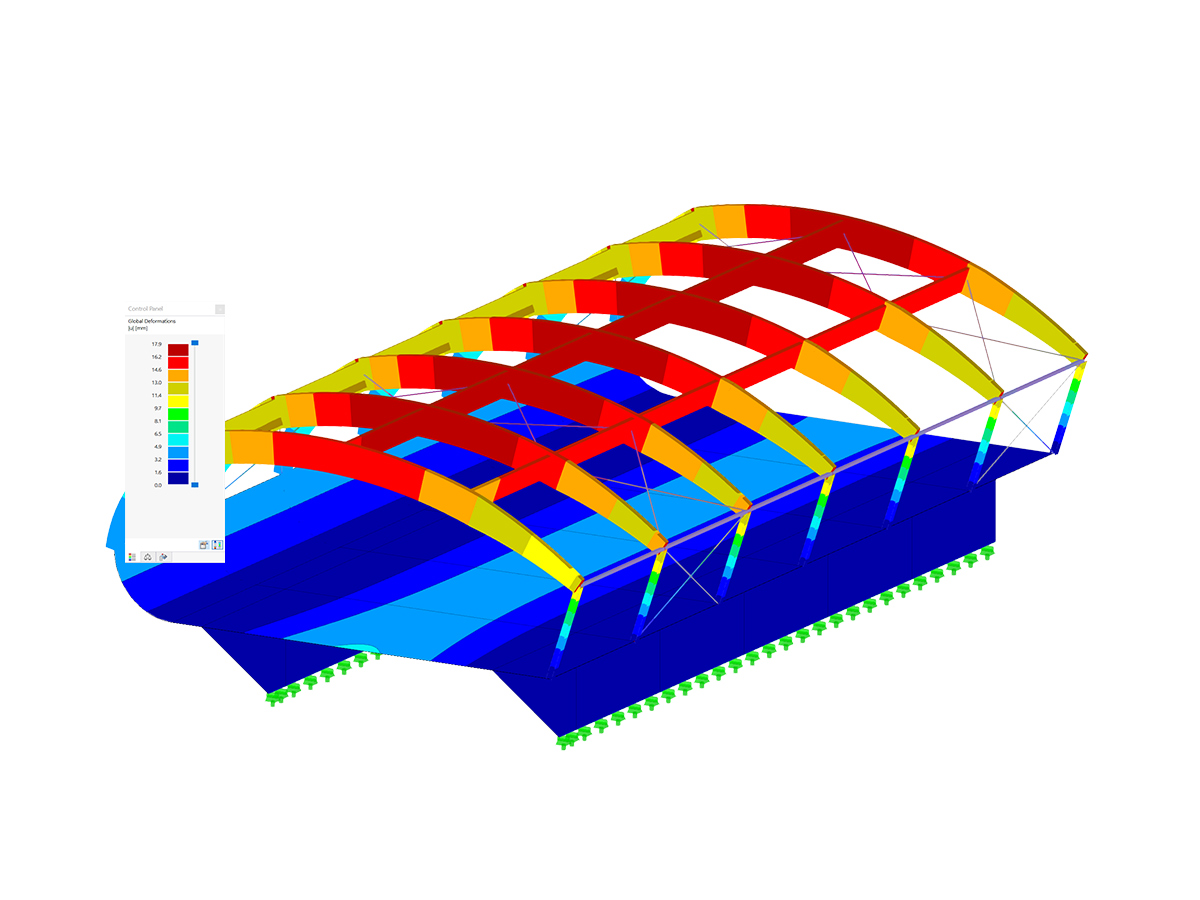
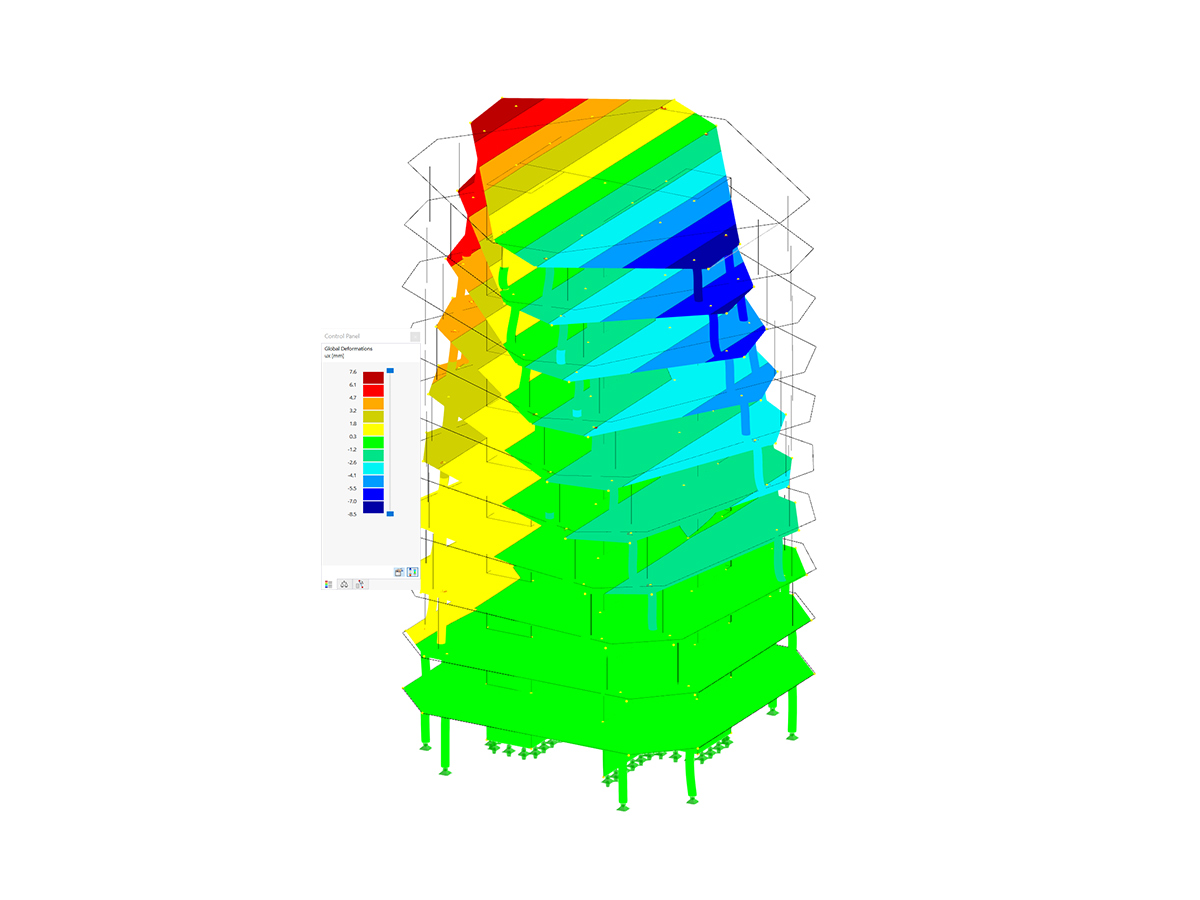
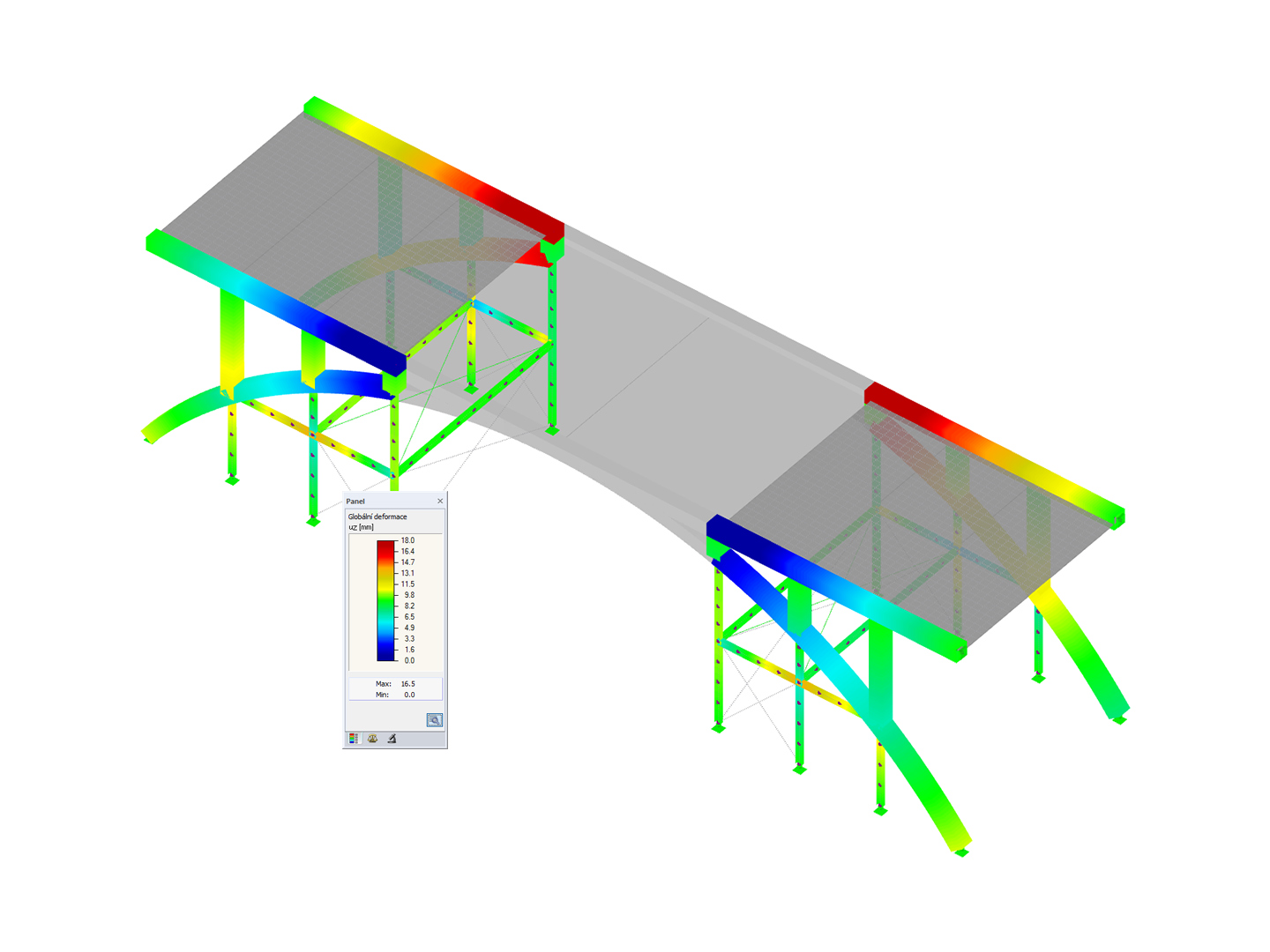
.png?mw=600&hash=49b6a289915d28aa461360f7308b092631b1446e)