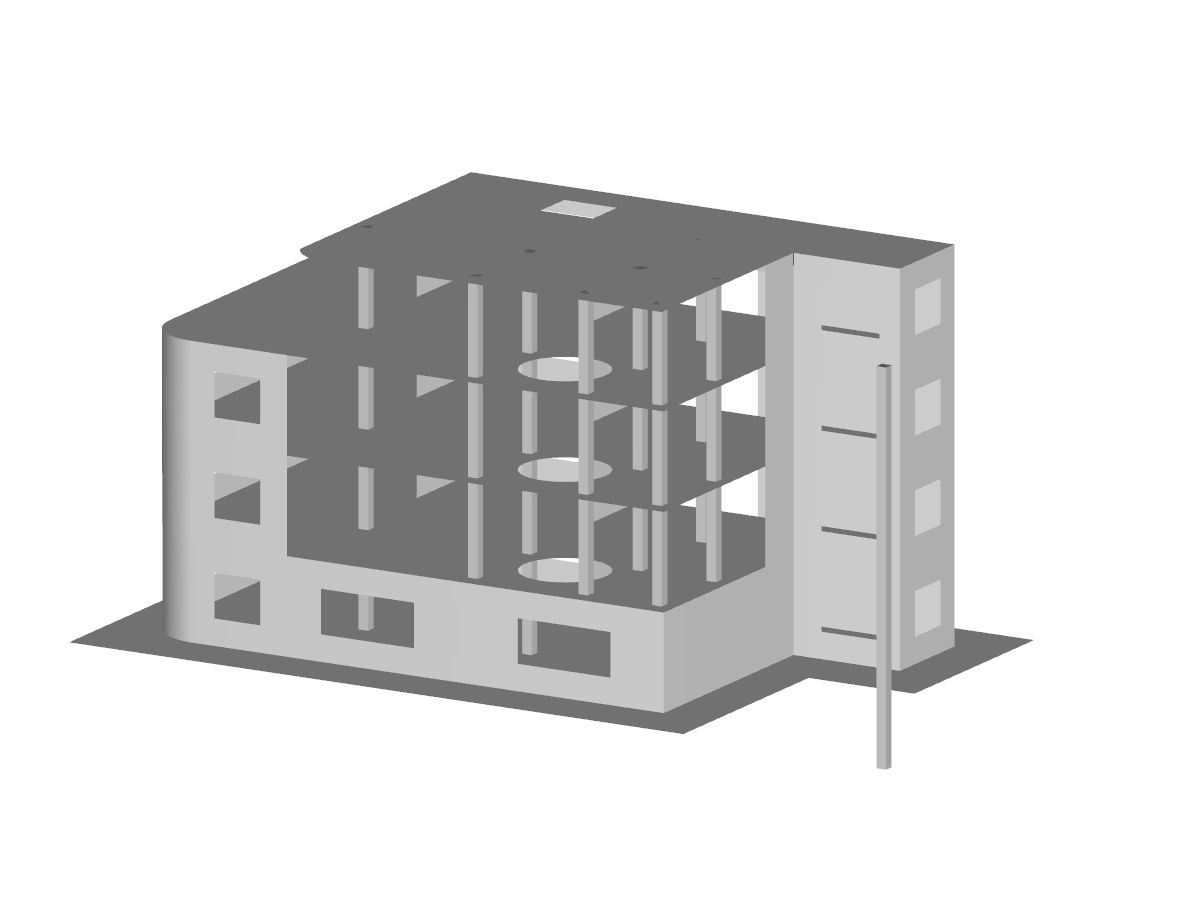
手动计算的假设条件
In den Berechnungsmodellen per Hand wird die Ermittlung dreiecks- oder trapezförmiger Stablasten der Unterzüge mittels Lasteinzugsflächen und mittels Tabellenwerken vorgenommen. Dabei wird lediglich unterschieden, wie die Platte an die jeweilige (Rand-)Linie anschließt. Läuft die Platte durch, so gilt dies als Einspannung an der Linie. Endet die Platte an dieser Linie, so ist es ein gelenkiger Anschluss. Im Schnittpunkt zweier senkrecht zueinander gestellter Linien mit derselben Anschlusseigenschaft (gelenkig oder eingespannt), beträgt die Neigung der Lastaufteilung 45°. Treffen Linien senkrecht aufeinander, die unterschiedliche Anschlusseigenschaften besitzen, so beträgt die Neigung der Zerlegungslinie 60°. Die Linie mit der Einspannung erhält aufgrund der höheren Steifigkeit mehr Last. Teileingespannte Lagerungen lassen sich mit einem Winkel zwischen 45° und 60° berücksichtigen. Befindet sich die gegenüberliegende parallele Linie weit genug von der betrachteten Linie entfernt, so ergibt sich eine Dreiecklast. Ist jedoch der Abstand der gegenüberliegenden Linie eher klein, so ergibt sich daraus eine Trapezlast.
Diese Herangehensweise geschieht unabhängig von der Stabsteifigkeit. Das heißt, dass die angenommene Beanspruchung bei einem kleinen und großen Unterzug dieselbe bleibt. Zudem wird dabei der Schubverbund zwischen Platte und Unterzug vernachlässigt und der Lastabtrag durch die Platte komplett vernachlässigt. Auch die günstige Wirkung der Exzentrizität bleibt unberücksichtigt.
Berechnungsbeispiel eines Unterzuges
Eine allseitig gelenkig gelagerte 20 cm dicke Platte mit Abmessungen von 5 m v 8 m soll in der Mitte durch einen Unterzug mit den Querschnittsabmessungen 30 cm · 40 cm verstärkt werden. Als Beanspruchung soll nur beispielhaft eine Gesamtlast von 10 kN/m² ohne Berücksichtigung des Eigengewichts wirken.
Handrechnung gemäß Schneider Bautabellen
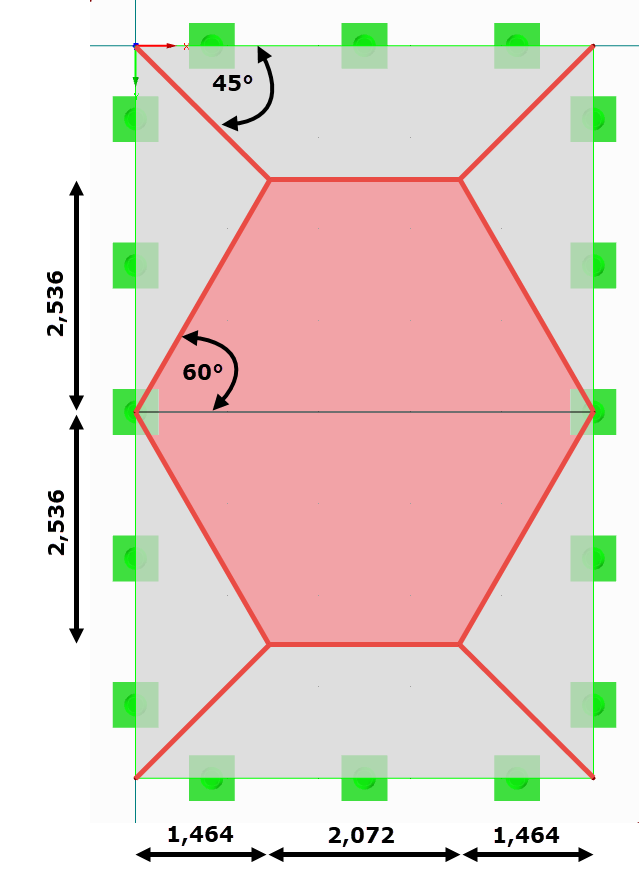
Da die Platte über den Unterzug hinwegläuft, wird der Lasteinzug des Stabes unter einem Winkel von 60° angenommen.
Die maximale Lastordinate einer Trapezlast ergibt sich zu:
0,634 · 10 kN/m² · 4,00 m = 25,36 kN/m
Da in beiden Feldern dieselben Randbedingungen vorliegen, muss die Last verdoppelt werden. Die Last beginnt mit 0 kN/m am Stabanfang und steigt über die Länge von 0,366 · 4,00 m = 1,464 m auf die maximale Lastordinate an. Wird der Unterzug damit belastet, so ergibt sich ein maximales Feldmoment mit My = 140,38 kNm.
RFEM-Berechnung
Bei der Modellierung wurde der Unterzug exzentrisch gesetzt. Die Oberkante des Stabes schließt an die Unterkante der Fläche an. Sämtliche Linienlager tragen nur Vertikalkräfte ab. Damit das System nicht kinematisch wird, wurde zusätzlich in einem Knoten ein Knotenlager mit einer Halterung in X- und Y-Richtung und einer Drehbehinderung um Z gesetzt. Die Belastung wurde als Flächenlast mit 10 kN/m² angenommen.
Als Ergebnis erhält man My = 16,77 kNm.
Hier muss jedoch noch erwähnt werden, dass neben dem Biegemoment auch ein Normalkraftverlauf mit max N = 254,48 kN affin zum Momentenverlauf entsteht. Dies resultiert daraus, dass die Beanspruchung nicht nur über Biegung, sondern auch über ein Kräftepaar (Druck in der Platte, Zug im Stab) abgetragen wird. In Feldmitte erreicht es den höchsten Wert und nimmt zum Rand hin parabelförmig ab.
Wird nun für beide Stäbe eine Stahlbetonbemessung durchgeführt, benötigt der Einzelstab eine untere Feldbewehrung von 10,13 cm², während der "echte" Unterzug mit 3,98 cm² auskommt.
Zur Verifikation der Handrechnung wurde das Mischsystem kopiert und anstelle der tatsächlichen Querschnittsabmessungen ein Starrstab verwendet. Bei diesem System erhält man ein maximales Biegemoment von 141,69 kNm was relativ genau mit der Handrechnung (140,38) übereinstimmt. Die Normalkraft kann mit 0,01 kN vernachlässigt werden.
概述总结
Bei sehr steifen Unterzügen beziehungsweise für die Ermittlung der Lagerkräfte bei vertikal unverschieblichen Lagern, liefert die Handrechnung übereinstimmende Ergebnisse zur FEM-Berechnung. Für genauere und wirtschaftliche Ergebnisse sollten jedoch FEM-Programme verwendet werden. Neben der oben beschriebenen Überschätzung der Stabschnittgrößen verhält es sich ähnlich mit den Plattenschnittgrößen. So kann es beispielsweise bei einem sehr schwachen Unterzug dazu kommen, dass anstelle der angenommenen Stützbewehrung mit dem FEM-Programm infolge der größeren Verformung noch ein positives Moment resultiert. Anstelle der angesetzten Stützbewehrung (an der Plattenoberseite) müsste bei der Berücksichtigung der realistischen Steifigkeiten noch eine Feldbewehrung (an der Plattenunterseite) angeordnet werden.















































_1.jpg?mw=350&hash=ab2086621f4e50c8c8fb8f3c211a22bc246e0552)




-querkraft-hertha-hurnaus.jpg?mw=350&hash=3306957537863c7a7dc17160e2ced5806b35a7fb)


.png?mw=600&hash=49b6a289915d28aa461360f7308b092631b1446e)