正如在 RFEM 6 中技术文章中确定混凝土板内力的用户自定义集成方法中所述，板内力和弯矩是对板厚度上的应力进行数值积分得出的（您可以在这里找到该文章）。 知识库 001817 )。 Wird ein nichtlineares Material verwendet, können Sie dabei in RFEM 6 zwischen der Gauß-Lobatto-Quadratur, der Trapezregel und der Simpsonregel wählen. Außerdem ist es möglich, die Anzahl der Integrationspunkte auf 3 bis 99 selbst festzulegen.
Die Theorie zu den Integrationsmethoden wird im Handbuch zu mehrschichtigen Flächen erklärt: 理论： 积分方法。 Dort finden Sie auch ein ähnliches Beispiel für eine dreischichtige, punktgestützte Platte: 计算举例： 积分方法。
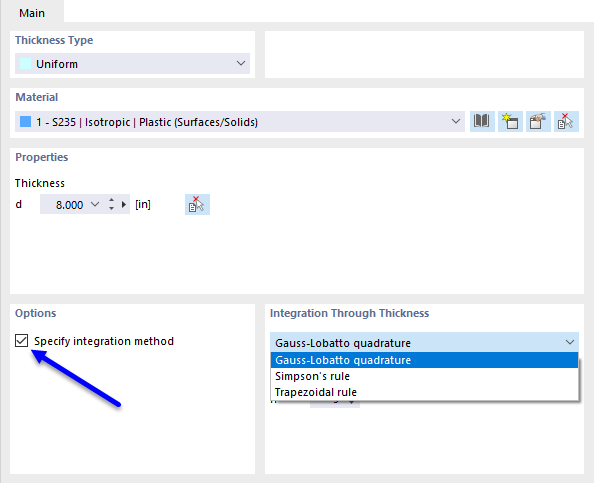
In diesem Beispiel soll für eine Stahlfaserbetonplatte gezeigt werden, welchen Unterschied die Verwendung der verschiedenen Integrationsmethoden und einer unterschiedlichen Anzahl an Integrationspunkten auf das Berechnungsergebnis hat. Dafür wird eine 5 m lange, 2 m breite und 30 cm dicke Platte betrachtet, für die das Materialmodell isotrope Beschädigung verwendet wird. Es wird eine Belastung von 13 kN/m² aufgebracht und die Netzdichte liegt bei 0,5 m.
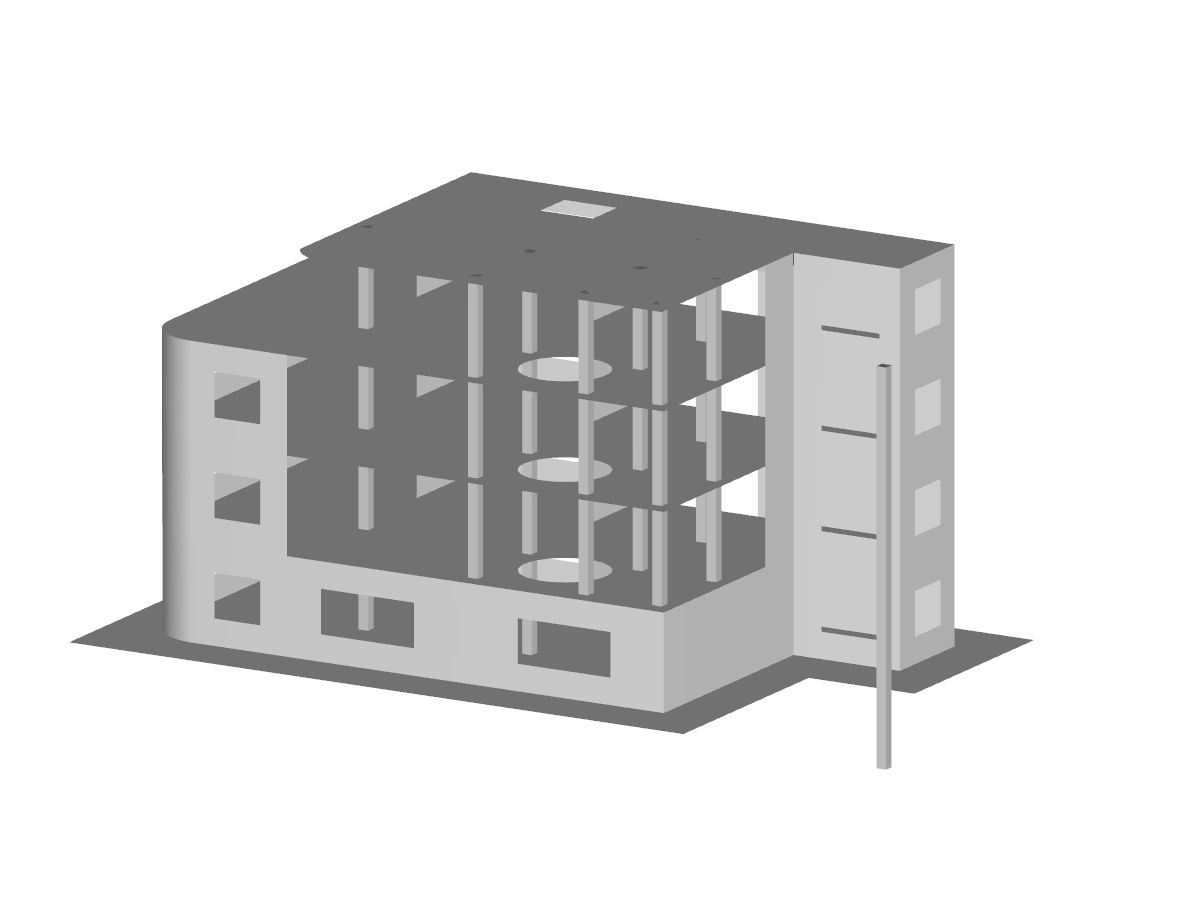
Die Integrationsmethode sowie die Anzahl der Integrationspunkte können in den Basisangaben der Plattendicke festgelegt werden.
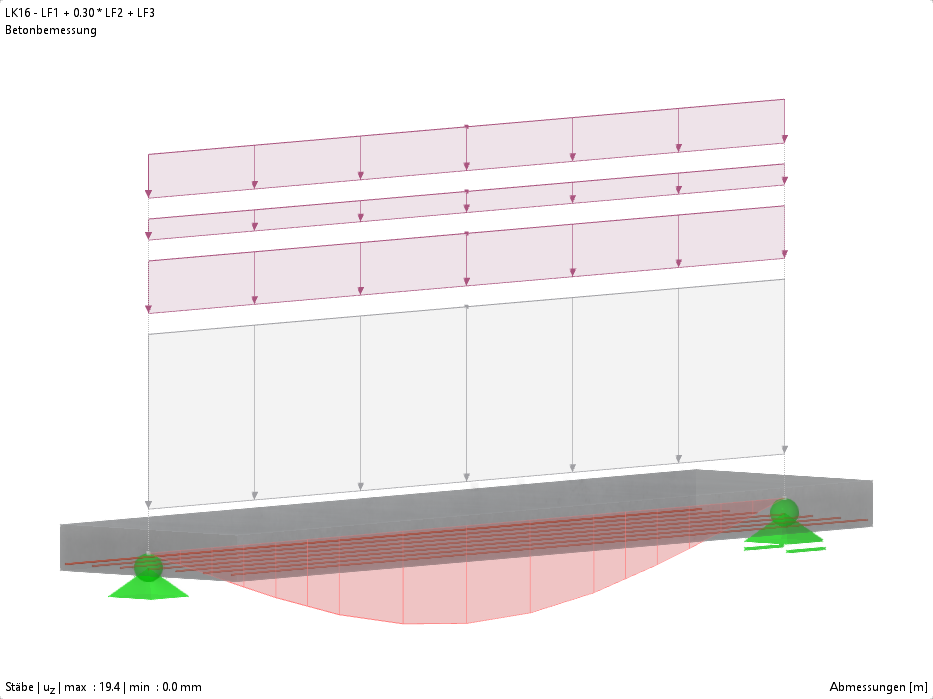
Die Berechnung liefert die folgenden Ergebnisse, wobei vor allem die Mitte der Platte (Rasterpunkt Nr. 28) betrachtet wird.
Für eine geringe Anzahl an Integrationspunkten ergeben sich sichtbare Abweichungen zwischen den einzelnen Integrationsmethoden. Besonders die Trapezregel weist eine geringere Genauigkeit auf. Bei einer höheren Anzahl nähern sich die Ergebnisse aller Integrationsmethoden jedoch einer festen Lösung an. Die in RFEM 6 standardmäßig verwendete Gauß-Lobatto-Quadratur mit 9 Integrationspunkten ist für die meisten Fälle ausreichend. Sollten Sie jedoch eine sehr hohe Belastung auf die Platte aufbringen, werden die Unterschiede zwischen den Integrationsmethoden noch deutlicher.
Insbesondere wenn Sie bis in den Fließbereich des Stahlfaserbetons rechnen, ist eine höhere Anzahl an Integrationspunkten sinnvoll, da das Materialverhalten auf diese Weise besser abgebildet werden kann. Das Spannungs-Dehnungsverhalten in diesem Bereich lässt sich schlecht durch Polynome approximieren, worauf jedoch die numerischen Integrationsmethoden beruhen. Deshalb kann es sich lohnen, in diesem Fall die Trapez- oder Simpsonregel zu verwenden, da diese jeweils auf einen kleineren Bereich angewendet und die Teilergebnisse anschließend addiert werden.
In diesem Fachbeitrag ist das Materialverhalten von Stahlfaserbeton erklärt: RFEM 中计算钢纤维混凝土的材料属性和工程计算
![跨度基于 [1] 中的图 5.2](/zh/webimage/039540/3493372/01_Abmessungen_EN.png?mw=512&hash=3cc425f1463bd5981b358d5889e3109e07ae1233)
.JPG?mw=350&hash=354dcaeb798219977d00c1979f12a0628654c9f0)
.png?mw=600&hash=49b6a289915d28aa461360f7308b092631b1446e)