Die Modellierung der Struktur für die Berechnung mit 7 Freiheitsgraden erfolgt über die Nutzung von Stäben in RFEM und RSTAB. Eine allgemeine Erklärung des Objektes finden Sie im Kapitel Stäbe des RFEM-Handbuchs. Flächen und Volumen können ebenfalls in einem Modell mit aktivierter Wölbkrafttorsion vorhanden sein. Diese Objekte verhalten sich dabei genauso wie bei einer Berechnung ohne Wölbkrafttorsion.
Berechnung von Stäben mit 7 Freiheitsgraden
Stäbe des Typs 'Balken' werden nach Aktivierung des Add-Ons Wölbkrafttorsion (7 Freiheitsgrade) automatisch mit 7 Freiheitsgraden berechnet, wenn ein Querschnitt mit aktivierter Wölbsteifigkeit zugeordnet ist. Nach der Berechnung werden für diese Stäbe zusätzliche Ergebnisse ausgegeben.
Berechnung von Stäben mit 6 Freiheitsgraden
Wird einem Stab des Typs 'Balken' ein Querschnitt zugeordnet, für den die Wölbsteifigkeit deaktiviert ist, so wird auch dieser Stab nur mit 6 Freiheitsgraden berechnet. Die Option zur Deaktivierung der Wölbsteifigkeit wird auch im Kapitel Querschnitte beschrieben.
Alle Stäbe eines anderen Stabtyps werden grundsätzlich mit 6 Freiheitsgraden berechnet. Diese Einschränkung des Stabtyps gilt unabhängig von der gewählten Option zur Aktivierung der Wölbsteifigkeit im Querschnitt.
Randbedingungen
Die Festlegung von Randbedingungen der 6 Freiheitsgrade ux, uy, uz, φx, φy und φz erfolgt mit der Definition von Knotenlagern.
Die Verwölbung an den Stabenden wird standardmäßig als unbehindert angenommen. Nutzen Sie Stabquersteifen, um Wölbfedern an den den Stabenden definieren. Diese können ebenfalls zur Abbildung eines Wölblagers genutzt werden.
Stablager können ebenfalls zur Definition der Randbedingungen genutzt werden.
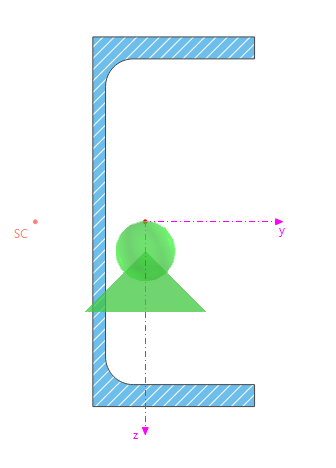
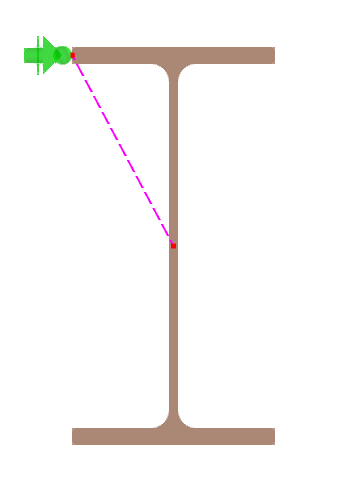
Zu beachten ist, dass alle Lager im Falle der Berechnung mit 7 Freiheitsgraden im Schwerpunkt des Querschnitts angesetzt werden. Je nach Lage des Schubmittelpunktes des für den Stab genutzten Querschnitts kann sich somit ein zusätzliches Torsionsmoment ergeben. Bei der Berechnung mit 6 Freiheitsgraden erfolgt die Lagerung der Querverschiebungen uy und uz des Stabes stets im Schubmittelpunkt. Gleiches gilt für den Anschluss angrenzender Bauteile, dies wird im Abschnitt Anschlusspunkt zu angrenzenden Bauteilen erklärt.
Übergangsbedingungen
Wie auch bei der Berechnung mit 6 Freiheitsgraden wird die Verbindung von Stäben in einem gemeinsamen Knoten als starr angenommen. Die globalen Verformungen und Verdrehungen sind somit an allen im Knoten zusammentreffenden Stabenden gleich. Definieren Sie Stabendgelenke um die Übergangsbedingungen der 6 Freiheitsgrade ux, uy, uz, φx, φy und φz festzulegen und von der starren Verbindung abzuweichen. Neben der Definition von Federwerten sind ebenso auch Nichtlinearitäten möglich. Im Kapitel Stabendgelenke des RFEM-Handbuchs wird die Funktion der Stabendgelenke beschrieben.
Die Verwölbung an den Stabenden wird standardmäßig als unbehindert angenommen. Das Bimoment und die Verwölbung werden daher nicht an angrenzende Stäbe übertragen. Eine Kontinuität der Verwölbung und des Bimoments kann über die Modellierung von ungeteilten Stäben oder die Definition von Stabsätzen erfolgen. Mehr Informationen dazu finden Sie im Kapitel Stabsätze.
Anschlusspunkt zu angrenzenden Bauteilen
Schließen andere Objekte an einen mit 7 Freiheitsgraden zu berechnenden Stab an, so wird der Verbindungspunkt stets im Schwerpunkt angenommen. Querlasten aus einem anschließenden Bauteil oder Lager erzeugen somit je nach Lage des Schubmittelpunktes ein zusätzliches Torsionsmoment.
Bei der Berechnung von Stäben mit 6 Freiheitsgraden werden Querkräfte aus anderen Bauteilen dagegen im Schubmittelpunkt eingeleitet. Normalkräfte aus anderen Bauteilen werden in beiden Fällen im Schwerpunkt übertragen.
Soll der Anschluss an einem anderen Punkt erfolgen, so können Sie die Verbindung mit Starrstäben modellieren oder Stabexzentrizitäten nutzen.