Nestabilita | únor 2023

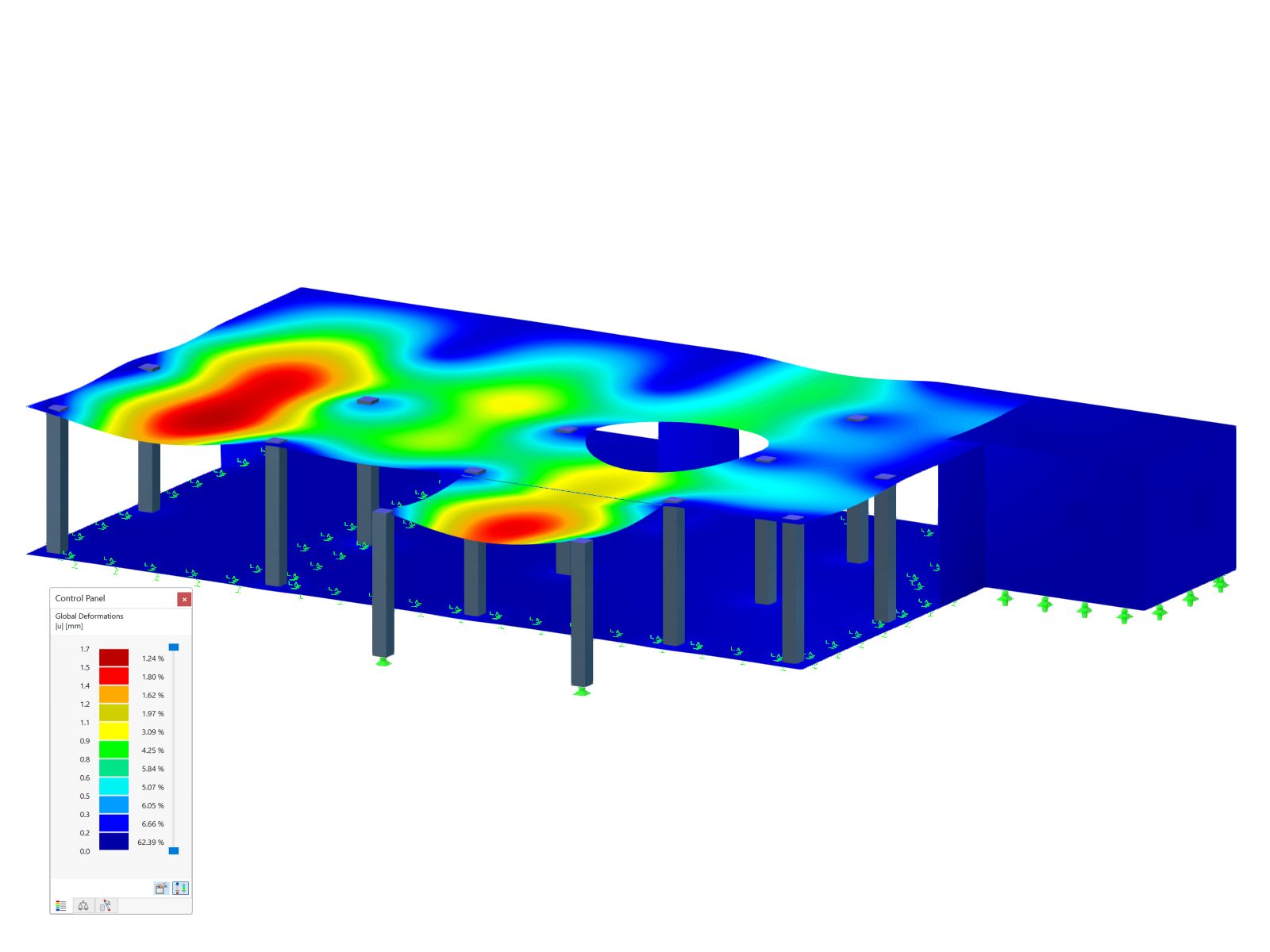
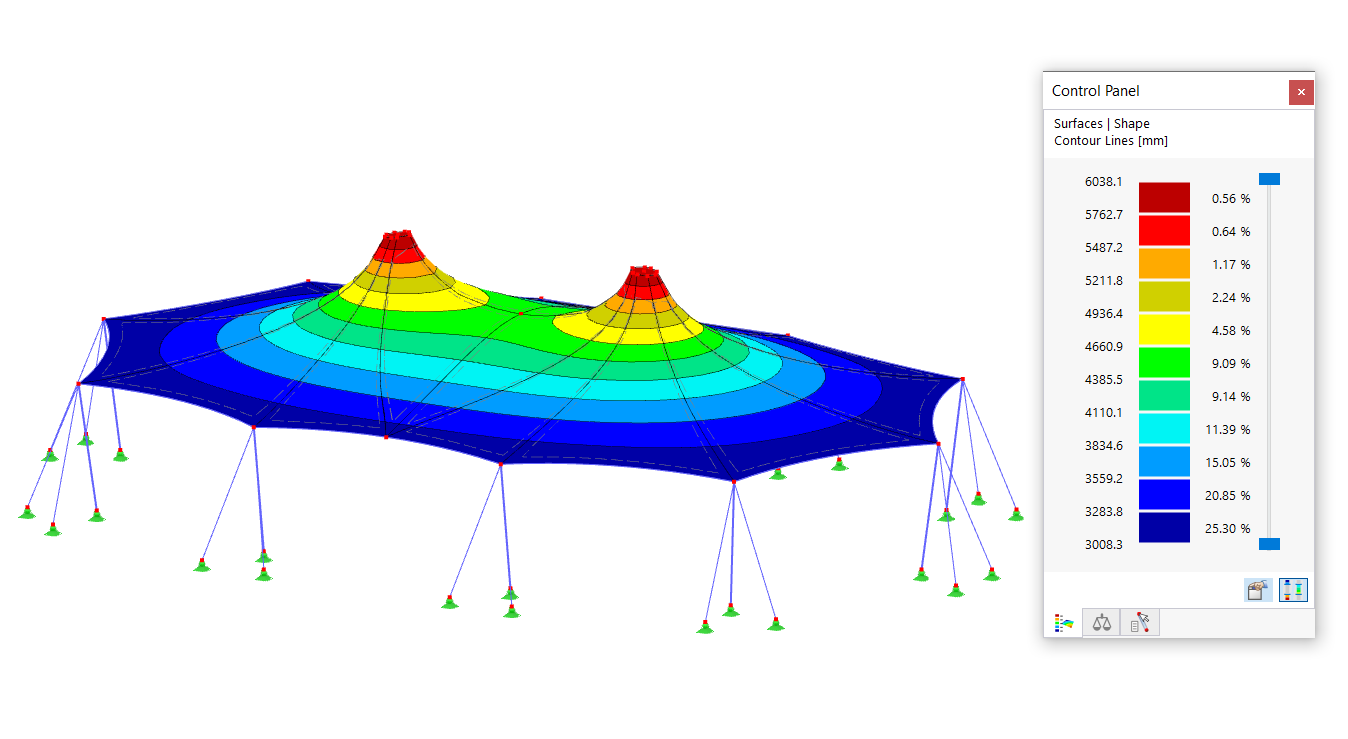
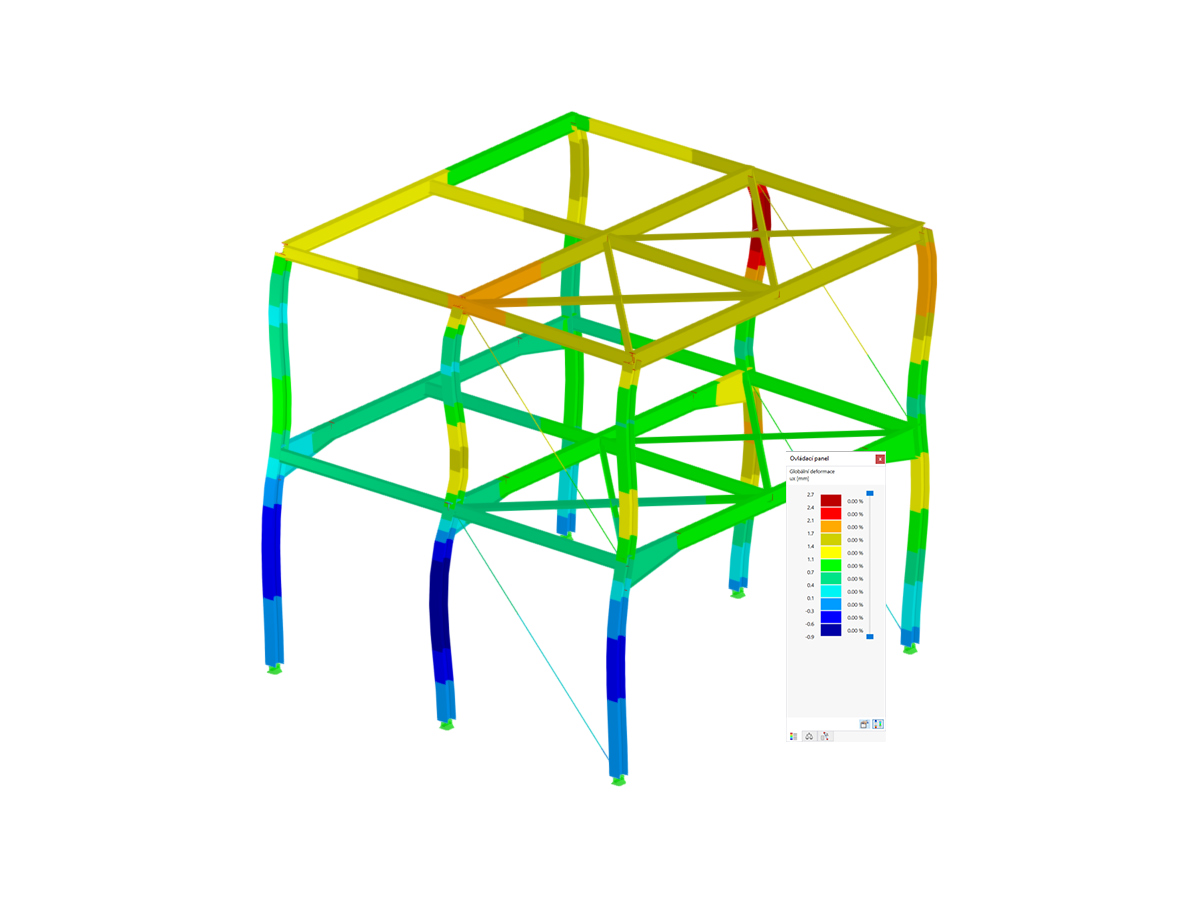
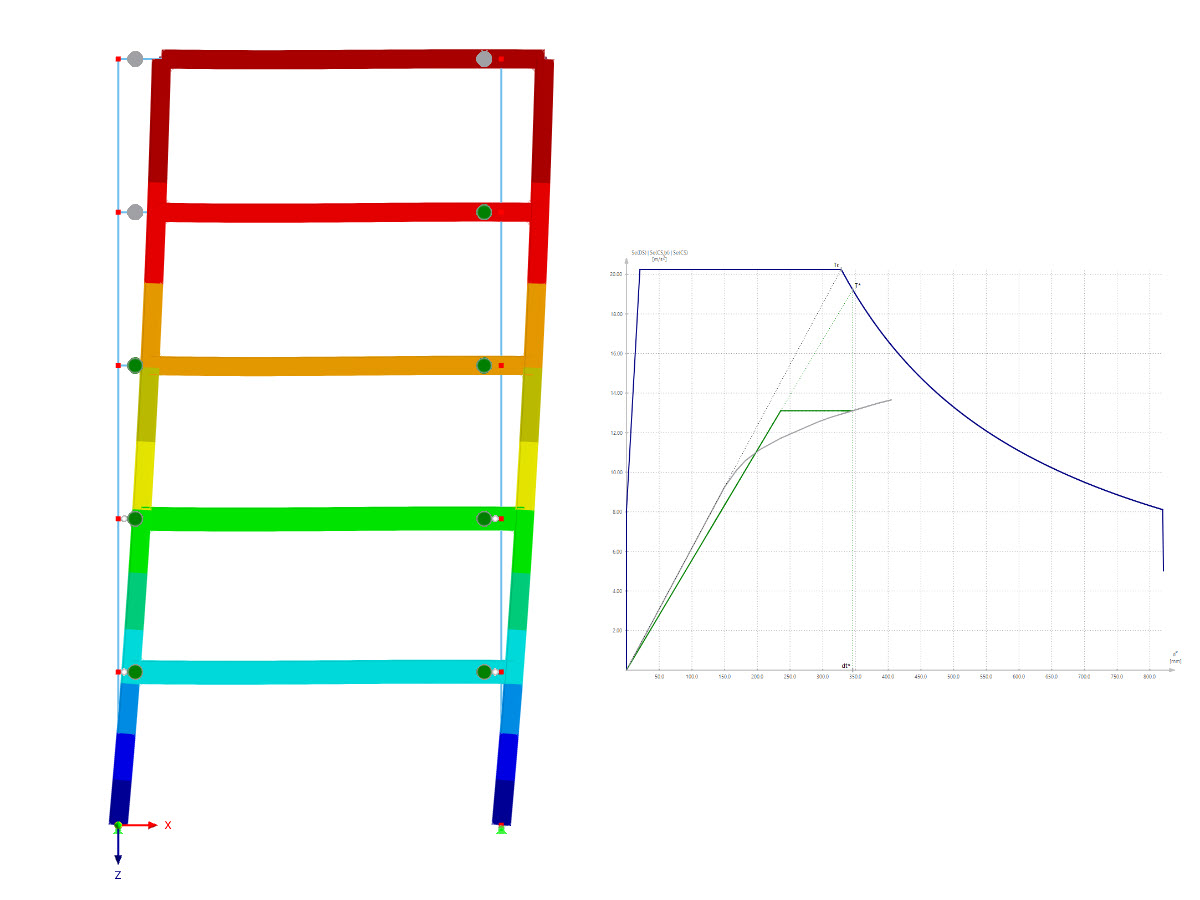
Přerušení výpočtu kvůli nestabilnímu systému může mít různé příčiny. Může na jedné straně naznačovat „skutečnou“ nestabilitu v důsledku přetížení systému a na druhé straně může být tato chybová zpráva způsobena nepřesnostmi v modelování. Níže naleznete možné postupy při hledání příčiny nestability.

1. Kontrola modelování

Nejprve je třeba zkontrolovat, zda je systém z hlediska modelování v pořádku. K tomu slouží v RFEM nebo RSTAB kontrola modelu (Nástroje → Kontrola modelu). Pomocí těchto nástrojů lze například zjistit identické uzly nebo překrývající se pruty a případně je vyčistit.

FAQ

FAQ 005345 | Můj model v programu RFEM 6 / RSTAB 9 je nestabilní. Čím by to mohlo být?

Možnosti kontroly modelu

Konstrukci lze také vypočítat například při čisté vlastní tíze v zatěžovacím stavu podle teorie prvního řádu. Pokud zde existují výsledky, je konstrukce z hlediska modelování stabilní. Pokud tomu tak není, jsou níže uvedeny nejčastější příčiny:

• Nesprávně definovaná podpory / Neexistující podpory

To může vést k nestabilitě, protože systém není držatelný ve všech směrech. Proto je nutné, aby podmínky podpor odpovídaly systému i vnějším okrajovým podmínkám. Staticky neurčité systémy mohou také vést k přerušení výpočtu kvůli nedostatečným okrajovým podmínkám.

Kinematický systém - nosník o jednom poli bez pevné podpory

• Kroucení prutů kolem vlastní osy

Pokud se pruty kroutí kolem vlastní osy a tedy nejsou drženy kolem vlastní osy, může to vést k nestabilitě. Příčinou jsou často nastavení kloubů prutů. Například může být zavedeno kroucení na začátku i na konci prutu.

Zadání torzních kloubů na počátečním a koncovém uzlu

• Chybějící spojení prutů

Zvláště u větších a složitějších modelů se může snadno stát, že některé pruty nejsou propojeny a „visí v prostoru“. Zanesení křížení prutů, které by se měly řezat, může také vést k nestabilitě. Řešením je kontrola modelu „Křížení nepřipojených prutů“, která hledá pruty, jež se kříží, ale nemají společný uzel v průsečíku.

• Nepřítomnost společného uzlu

Uzly jsou na první pohled na stejném místě, ale při bližším pohledu se minimálně liší. Častou příčinou je import z CAD, který lze vyčistit pomocí kontroly modelu.

Výsledek kontroly modelu na identické uzly

• Vznik řetězu kloubů

Příliš mnoho kloubů prutu na jednom uzlu může způsobit řetěz kloubů, což vede k selhání výpočtu. Na jednom uzlu lze definovat pouze n-1 kloubů se stejným stupněm volnosti vzhledem ke globálnímu souřadnému systému, kde „n“ je počet připojených prutů. Totéž platí pro liniové klouby.

Kinematický systém z důvodu nadměrného počtu kloubů konců prutů na uzlu

2. Kontrola ztužení

Nedostatečné ztužení také vede k přerušení výpočtu v důsledku nestability. Proto by vždy mělo být kontrolováno, zda je konstrukce dostatečně ztužena ve všech směrech.

Chybějící ztužení

3. Numerické problémy

K tomuto bodu lze uvést následující příklad: Kloubový rám je ztužen tažnými pruty. Kvůli zkrácení stojin v důsledku svislého zatížení obdrží tažné pruty během prvního výpočtového kroku malé tlakové síly. Ty jsou ze systému odstraněny (protože mohou zachytit pouze tah). Ve druhém výpočtovém kroku je model bez těchto prutů nestabilní.

Existuje několik způsobů, jak tento problém řešit. Tažným prutům můžete přiřadit předpětí (zatížení prutů) k „eliminaci“ malých tlakových sil, přidělit prutům malou tuhost nebo nechat pruty během výpočtu postupně odstraňovat. Tento výpočetní postup je v RSTAB 9 automatizovaný, v RFEM 6 ho lze volitelně povolit.

Parametry výpočtu v programu RFEM 6

4. Hledání příčiny nestability

• Automatická kontrola modelu s grafickým výstupem

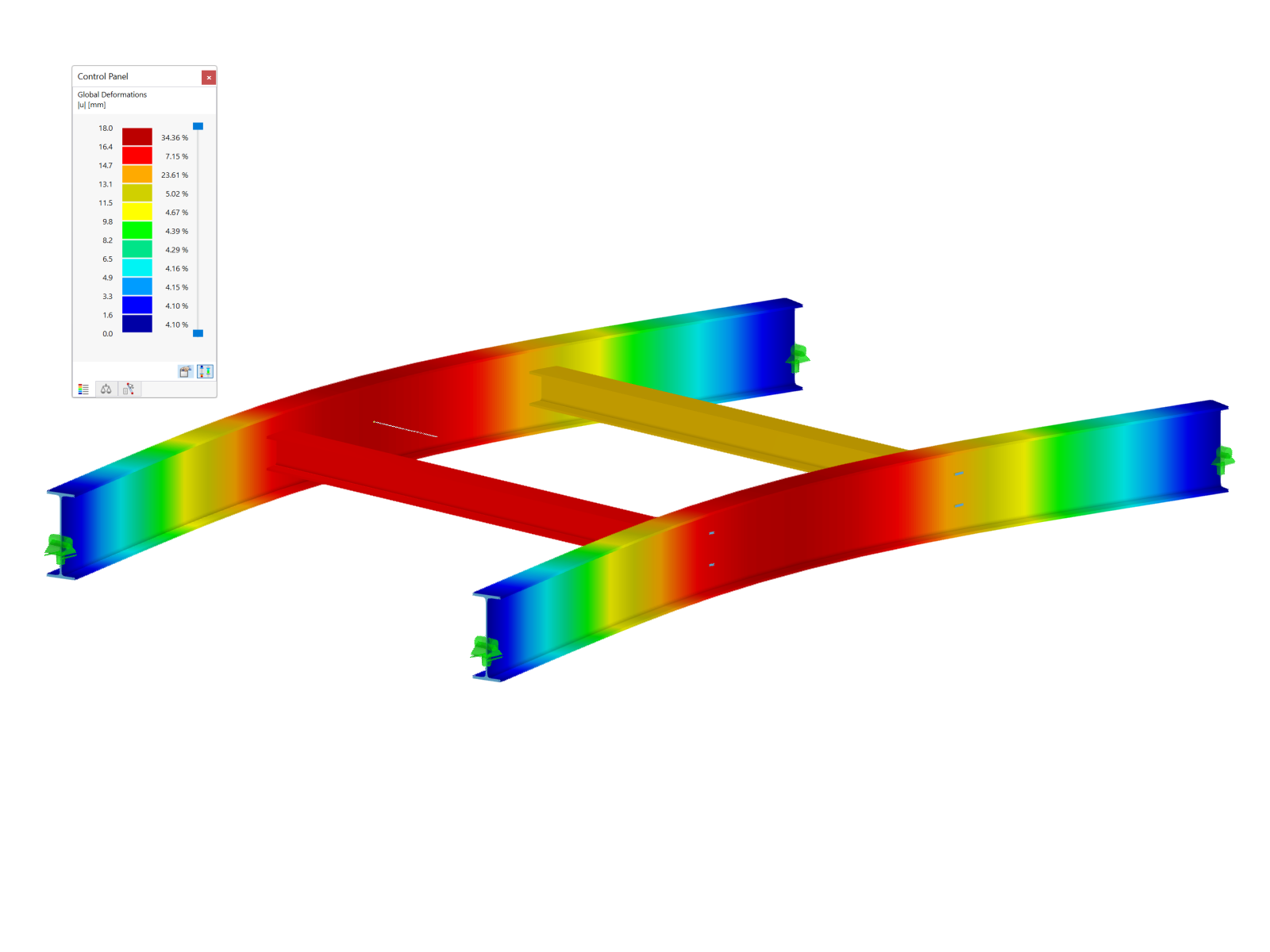
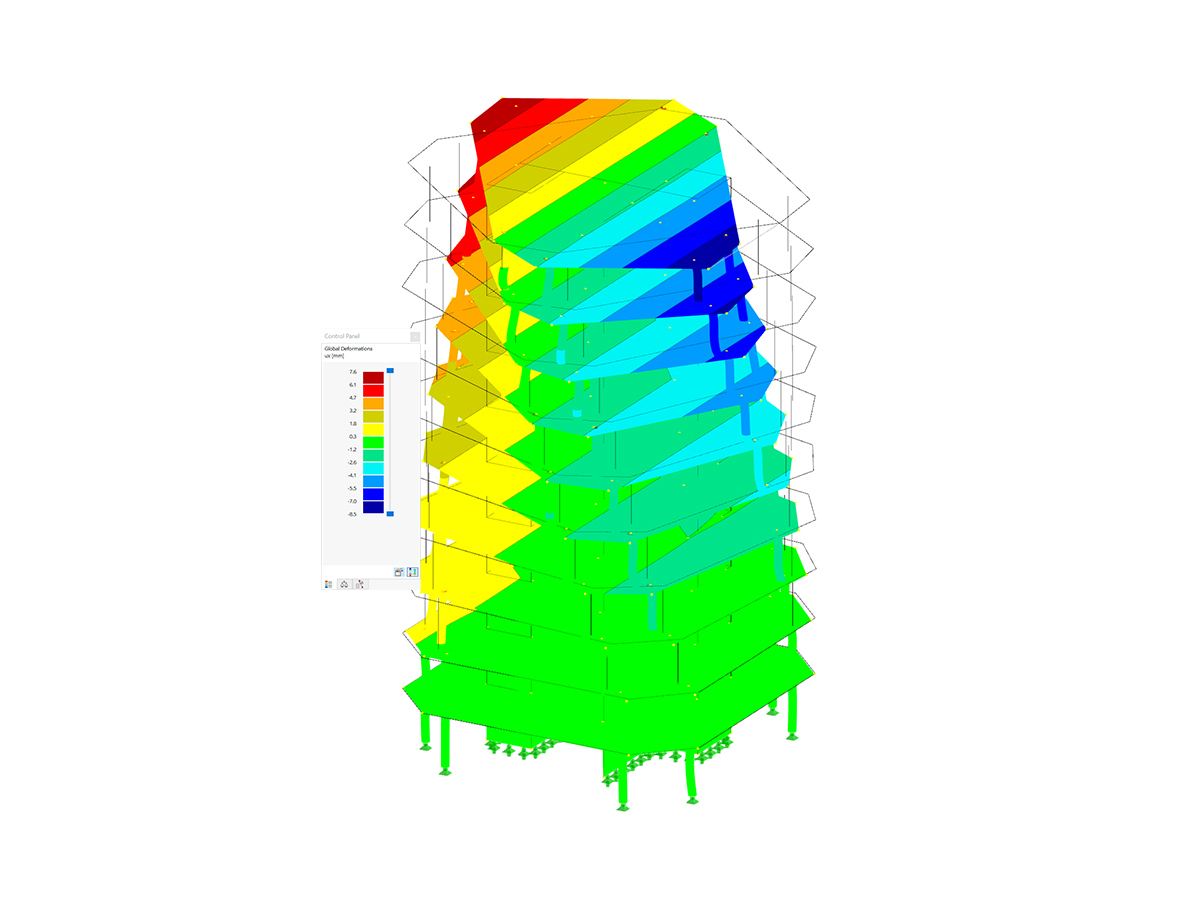
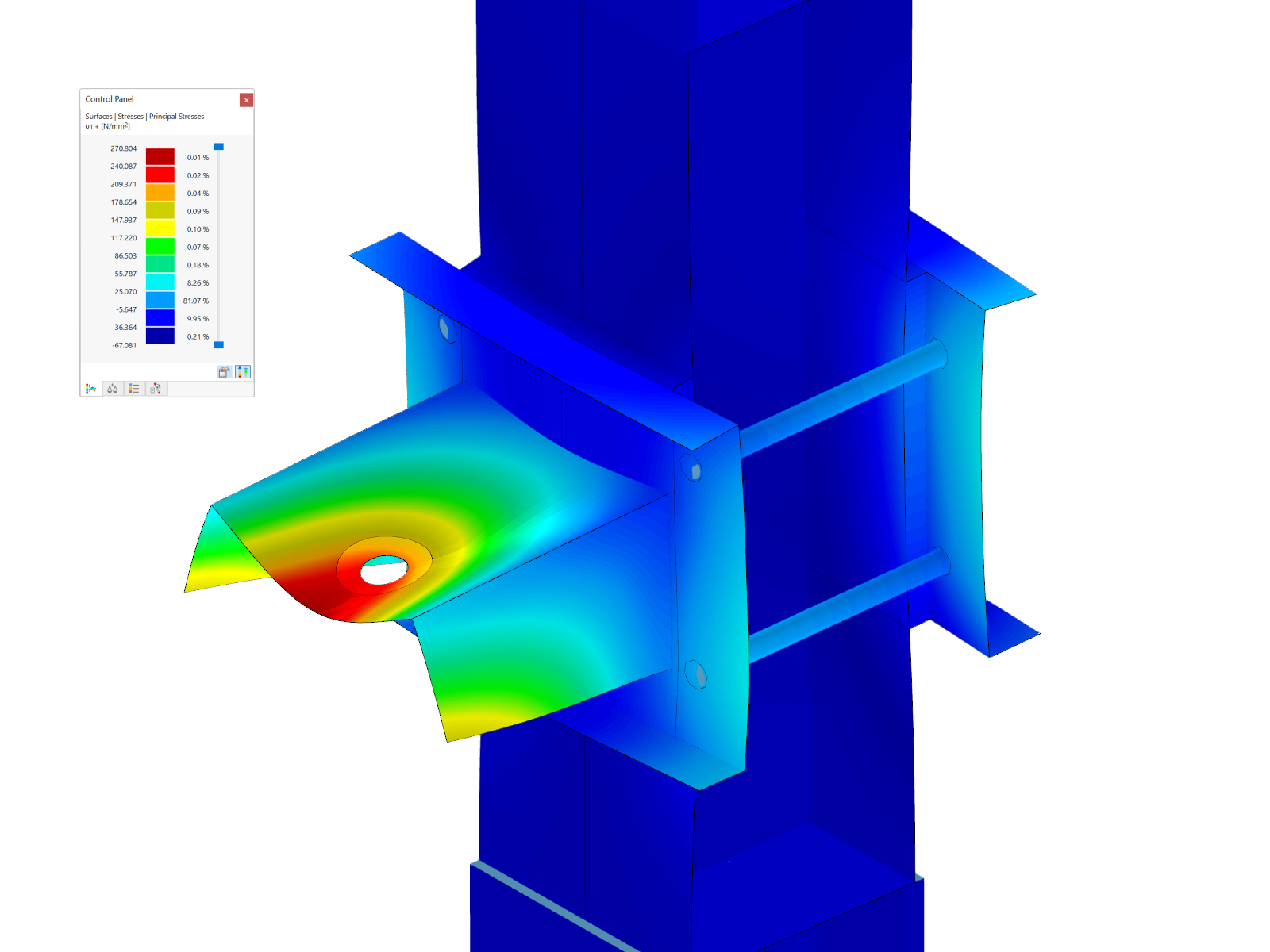
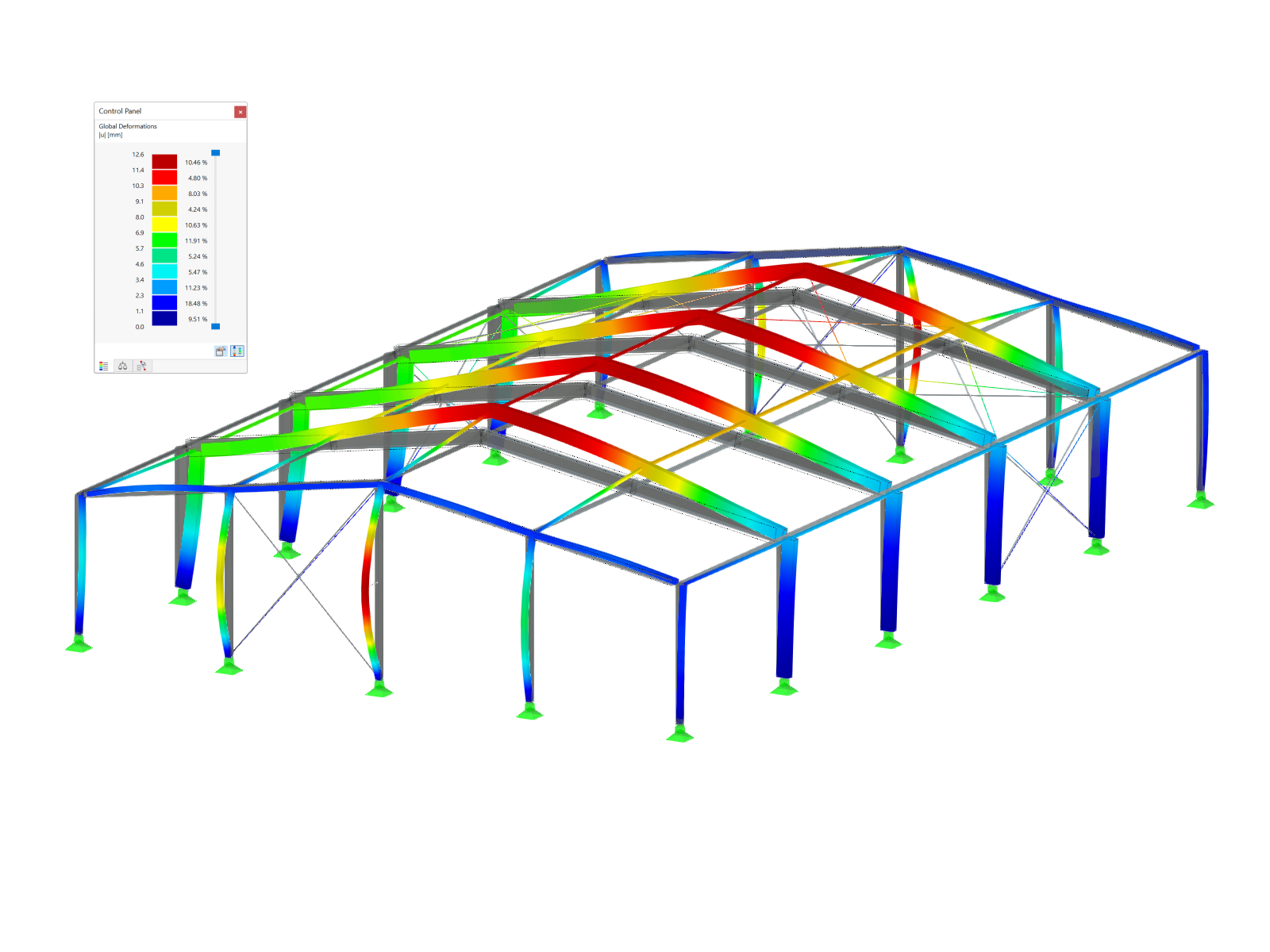
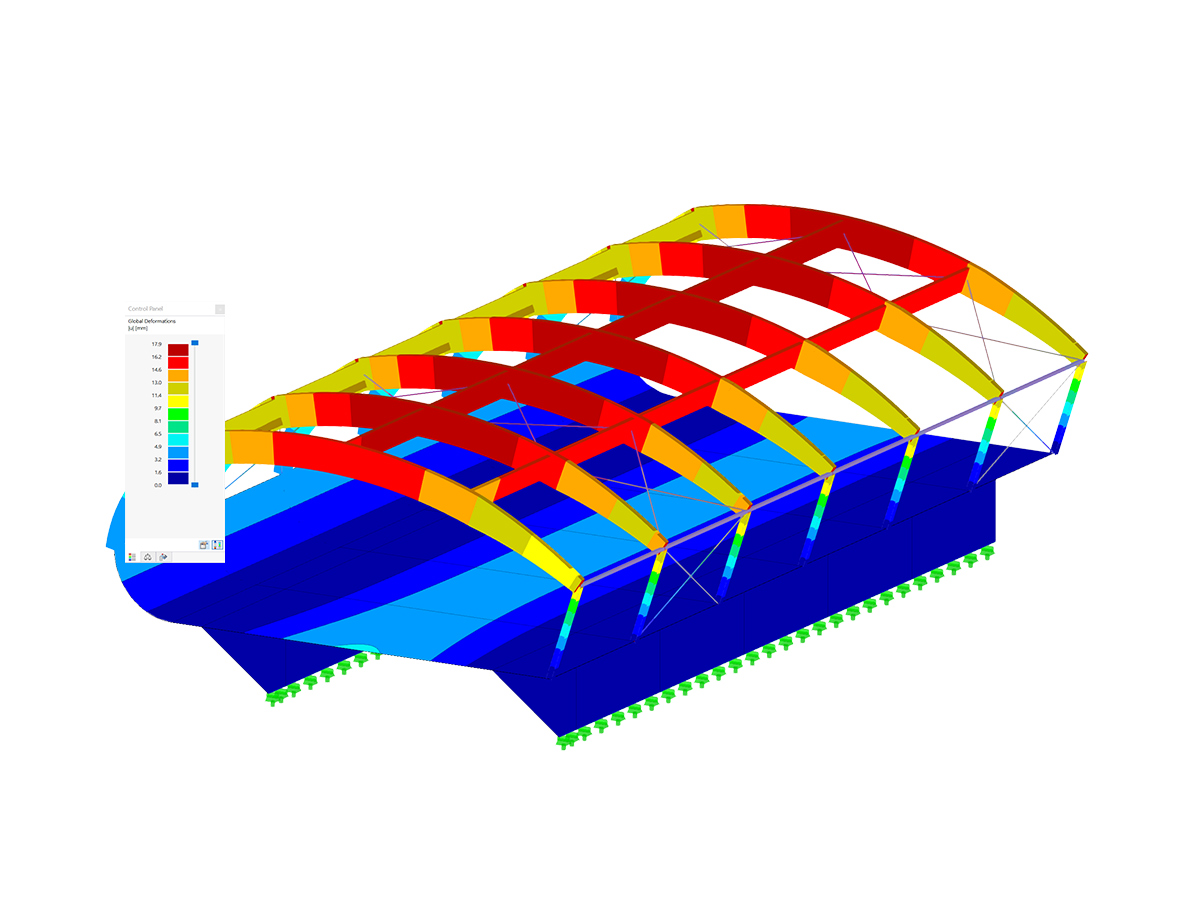
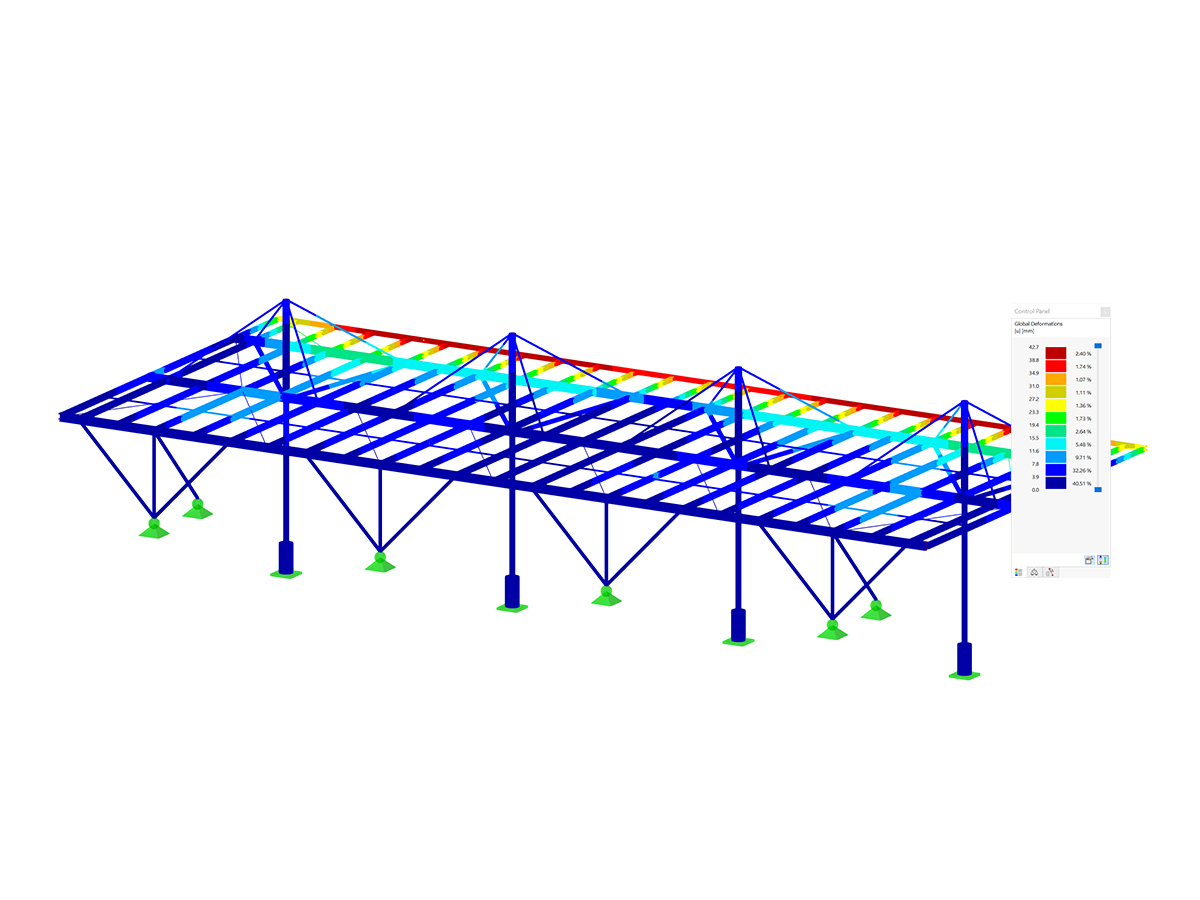
Pro grafické zobrazení příčiny nestability může pomoci přídavný modul Stabilita konstrukce. Pomocí možnosti „Vypočítat bez zatížení pro prokázání stabilizace pomocí vlastního tvaru“ lze vypočítat zdánlivě nestabilní systémy. Na základě dat konstrukce je provedena analýza vlastních čísel, takže je jako výsledek graficky zobrazen nestabilní prvek.

Grafické zobrazení nestability

• Problém s rozvětvením

Pokud lze vypočítat zatěžovací stavy nebo kombinace zatížení podle teorie prvního řádu a výpočet selže až od teorie druhého řádu, jedná se o problém se stabilitou (kritický zatěžovací součinitel menší než 1,00). Kritický zatěžovací součinitel udává, jakým faktorem je třeba zatížení vynásobit, aby se model pod příslušným zatížením stal nestabilním (např. vybočení). Z toho vyplývá: Kritický zatěžovací součinitel menší než 1,00 znamená, že systém je nestabilní. Jen pozitivní kritický zatěžovací součinitel větší než 1,00 umožňuje konstatovat, že zatížení v důsledku předepsaných normálových sil vynásobené tímto faktorem vede ke ztrátě stability stabilního systému. Pro nalezení „slabého místa“ se doporučuje následující postup, který vyžaduje přídavný modul Stabilita konstrukce.

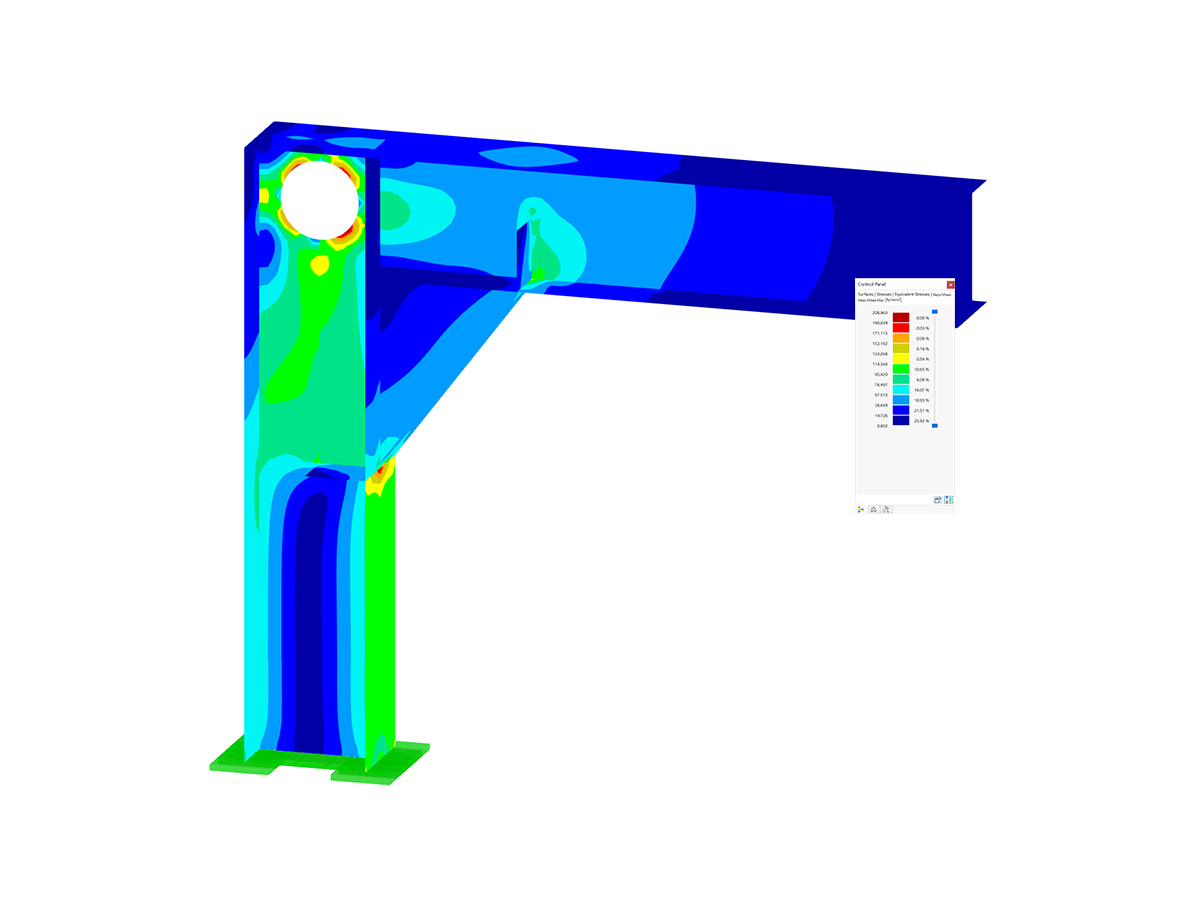
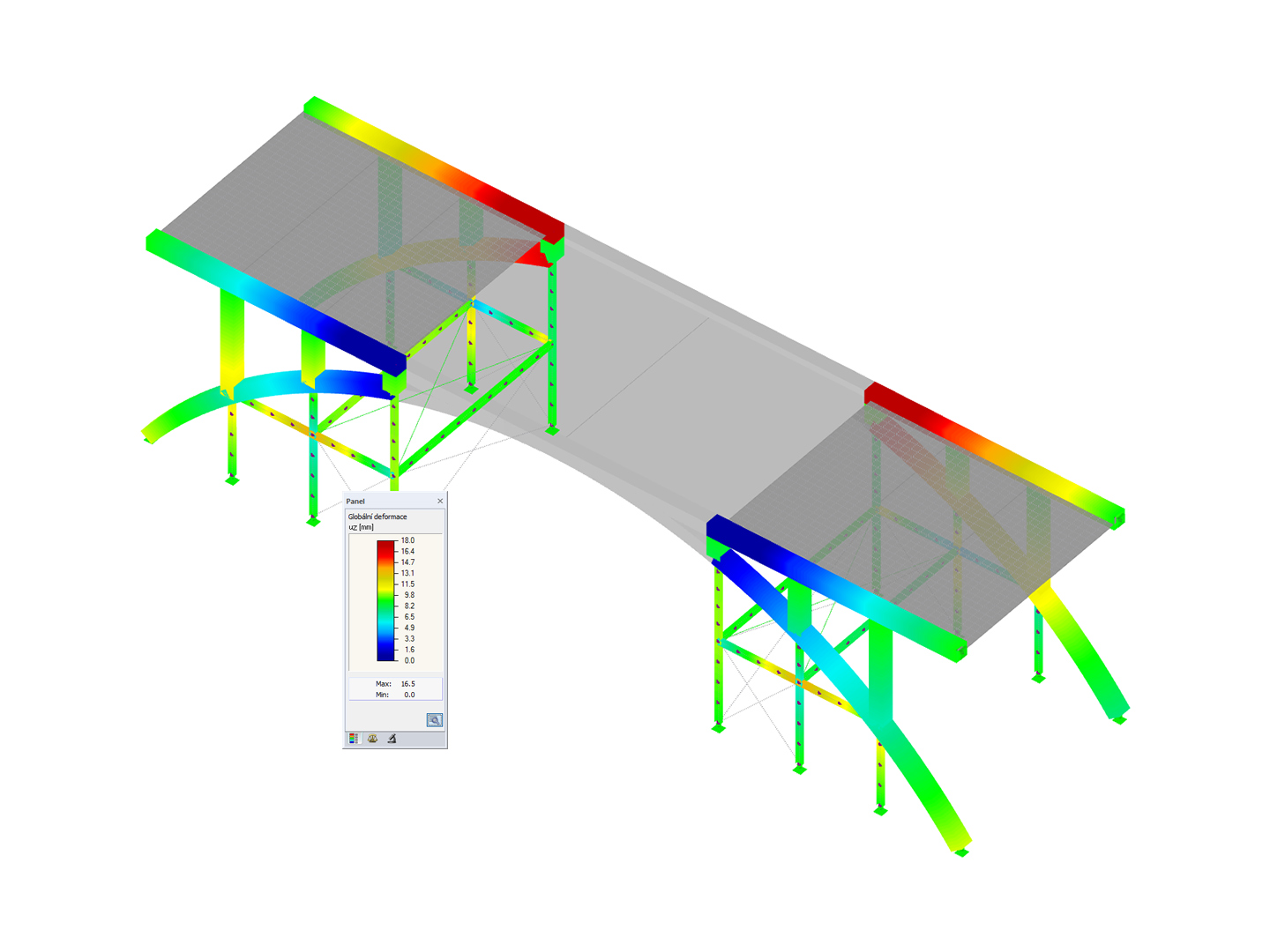
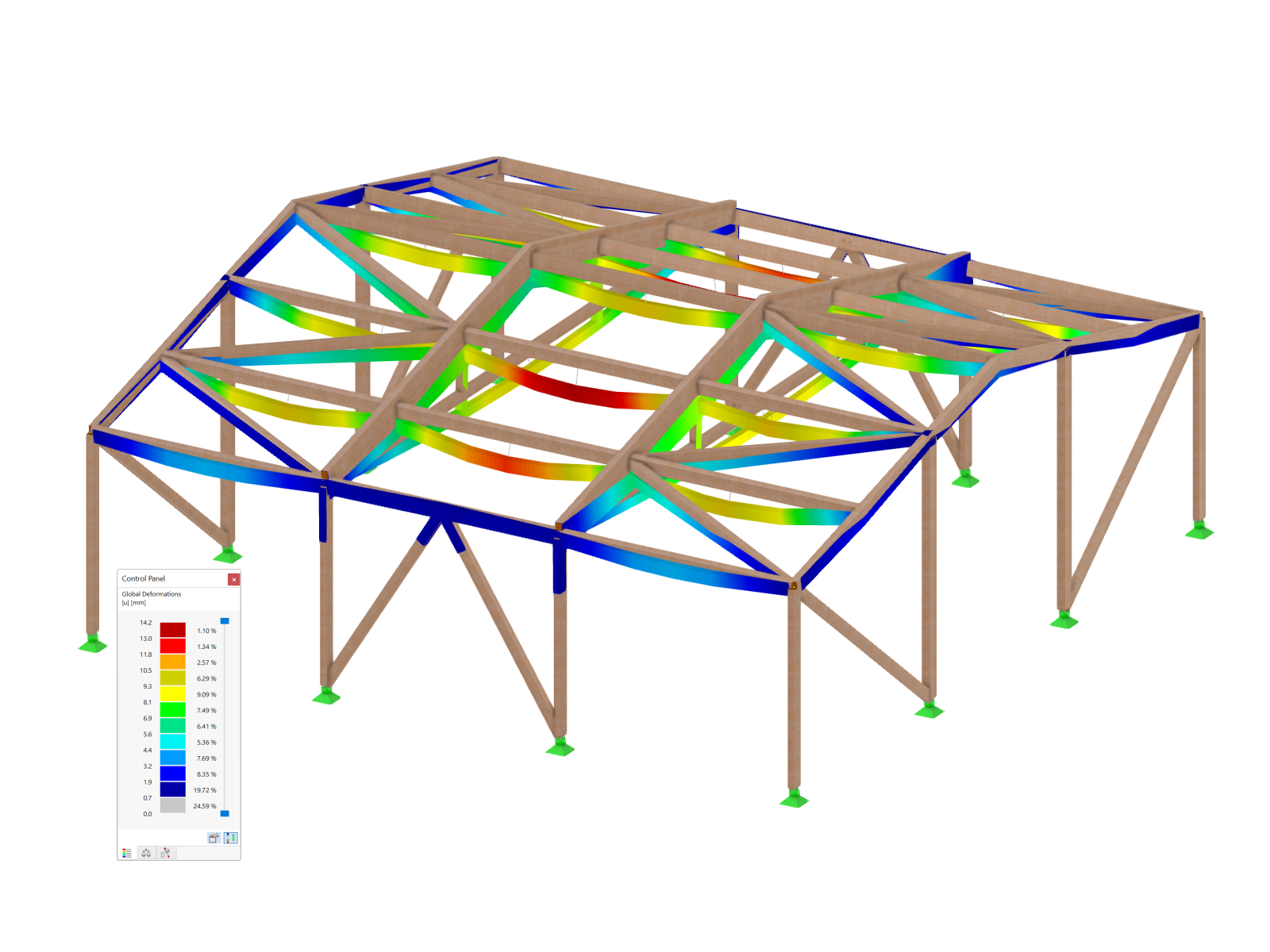
Nejprve by mělo být zatížení příslušné kombinace zatížení snižováno tak dlouho, dokud se kombinace zatížení nestabilizuje. Pomocný k tomu je zatěžovací součinitel v parametrech výpočtu kombinace zatížení. To odpovídá také manuálnímu určení kritického zatěžovacího součinitele, pokud přídavný modul Stabilita konstrukce není k dispozici. U čistě lineárních konstrukčních prvků může někdy stačit vypočítat kombinaci zatížení podle teorie prvního řádu a pomocí přídavného modulu zjistit kritické zatížení. Na základě grafického zobrazení vybočení nebo vyboulení této kombinace zatížení je možné identifikovat problémovou oblast v systému a přijmout opatření k nápravě.