Odpověď:
Pokud se mají konstrukční prvky počítat metodou konečných prvků (MKP), můžeme v programu RFEM volit mezi plochami a tělesy. Veliká výhoda ploch leží v době výpočtu, protože konečné prvky jsou definovány pouze v rovině plochy. Třetí rozměr, tedy tloušťka, se při výpočtu zohledňuje jako fyzikální vlastnost. Na plochu tak lze nahlížet jako na matematické zjednodušení. Plochy lze navíc snáze zesíťovat než tělesa (Jacobiho matice).
Rozlišujeme přitom dva typy plošných prvků. Zatímco v klasické teorii tenkých desek (Kirchhoff) se smykové deformace vlivem smykových sil zanedbávají, pro teorii silných desek (Reissner-Mindlin) je třeba uvažovat speciální rozšířené přístupy. U tenkých desek dominuje účinek čistého ohybu. Proto postačuje také zjednodušená teorie ohybu. Se zvyšující se tloušťkou roste podíl smykového účinku na nosném účinku. Chyba při zanedbání této části je nad určitou tloušťkou tak velká, že je nezbytně nutná vyšší teorie silné desky. To, zda se má deska považovat za "tenkou" nebo "silnou", nezávisí na poměru "rozměr k tloušťce" jednotlivých konečných prvků, ale na podmínkách ve statickém systému. Kromě tloušťky desky jsou rozhodujícími faktory především rozpětí (délka, šířka, poloměr), typ podepření, typ zatížení a také jejich rozdělení. Vzhledem k velkému počtu vlivů nelze stanovit závaznou hodnotu.
Na Obrázku 01 je znázorněna informace, která popisuje platnost příslušných prvků. Velikost „d“ je tloušťka dílce a „L“ délka dílce resp. vzdálenost mezi podepřeními. Poměr d/L udává, kdy který prvek platí pro analýzu. Pokud je poměr d/L velký, je deformace smykem kritickým faktorem a uživatel by měl upřednostnit použití těles. Pokud je poměr d/L malý, deformace smykem nemá žádný kritický vliv a plošné prvky jsou nejúčinnější volbou.
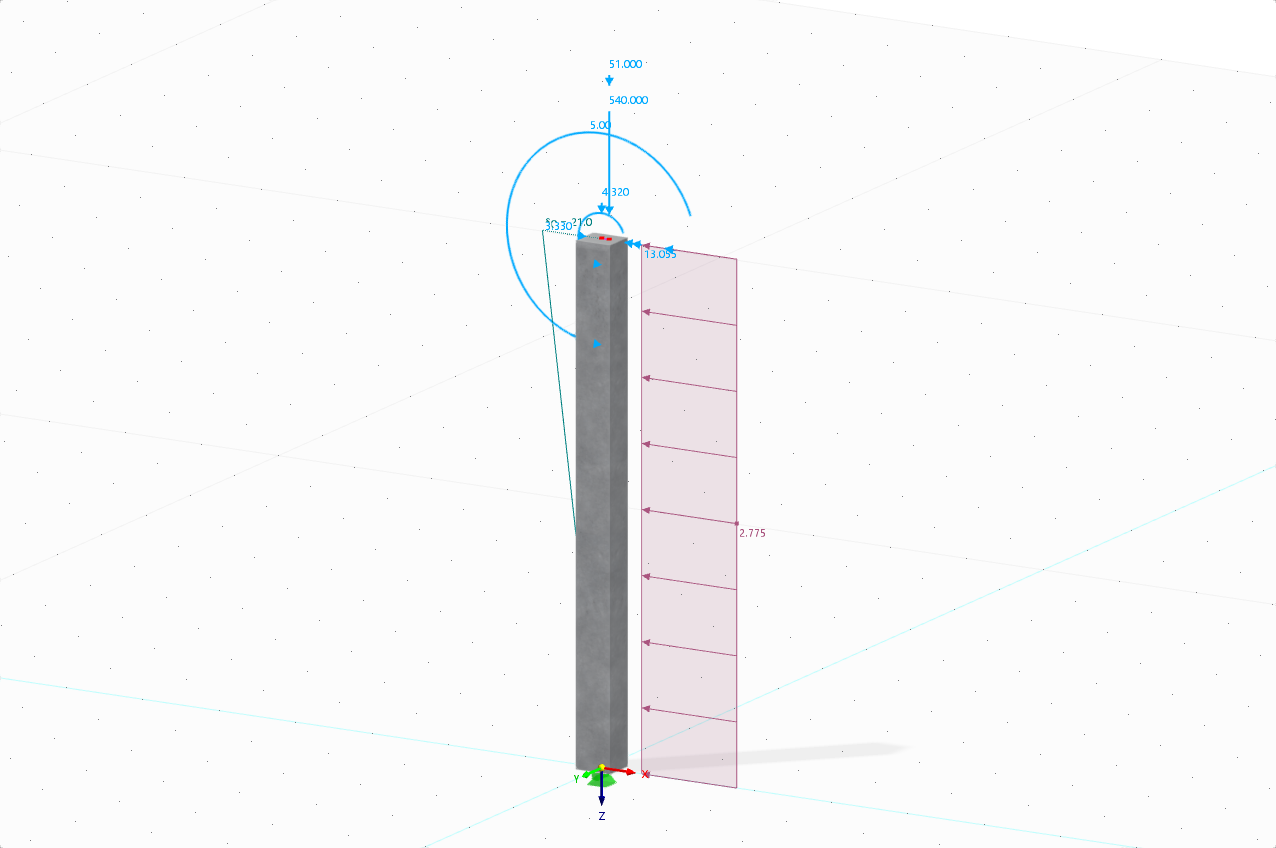
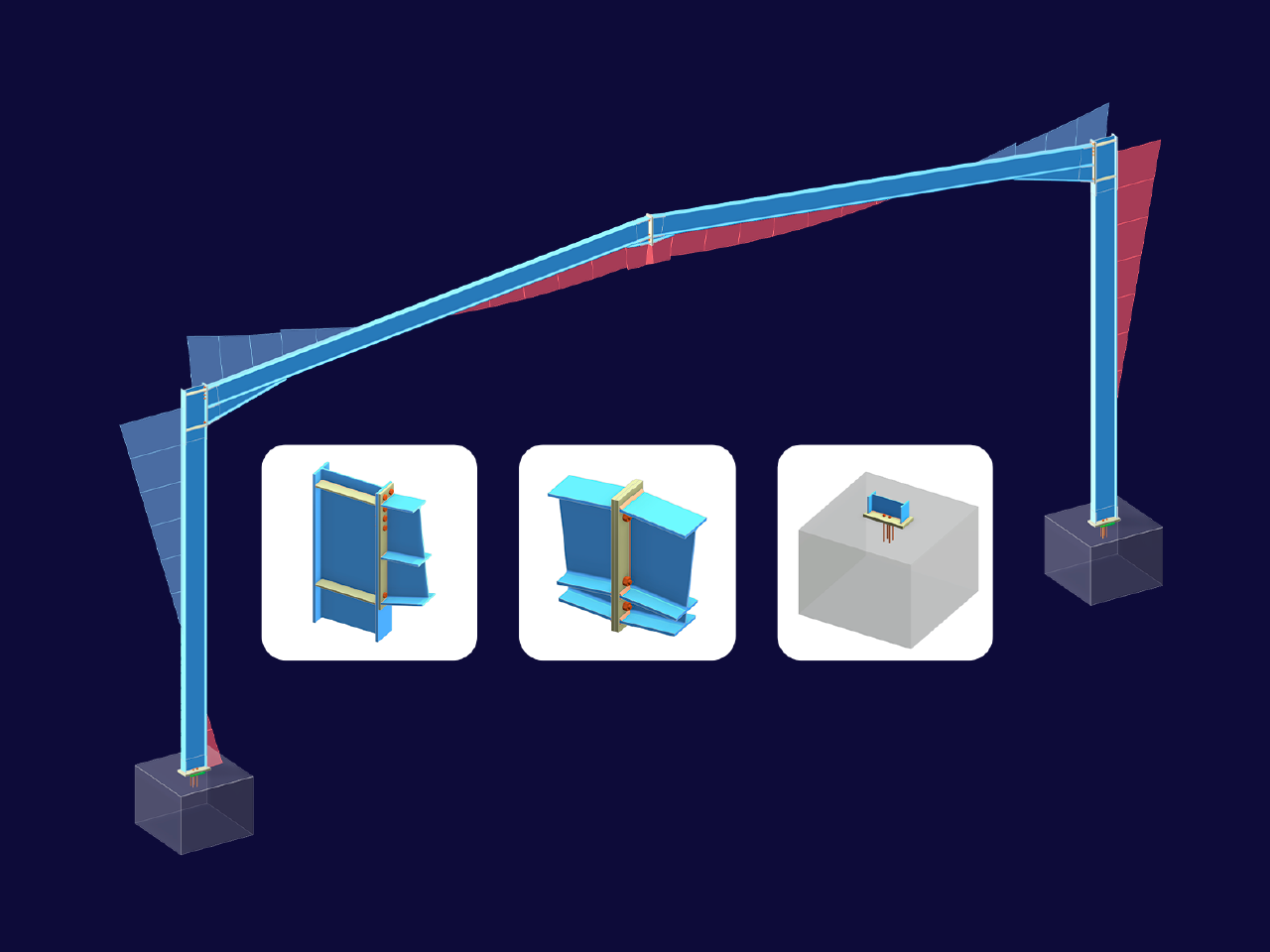
Na Obrázku 02 byly provedeny výpočty s různými prvky. Je zobrazený náhled, takže je možné interpretovat deformace v rovině obrázku. Při malém poměru d/L 0,2 se deformace u všech tří variant velmi dobře shodují. Při d/L = 0,4 již existují rozdíly mezi výpočtem tenké a silné desky. V extrémním případě d/L = 0,7 lze také pozorovat rozdíl mezi silnou deskou a tělesem. Zatížení byla zvolena tak, aby bylo dosaženo stejné deformace u všech těles, aby bylo dosaženo smysluplného výrazu.
.png?mw=350&hash=b023d6c658e181cb7d69028c0f3994dedab96fc5)
.jpg?mw=350&hash=bd355674e865e37d5548c329b8f5f0153cefe276)
.png?mw=600&hash=49b6a289915d28aa461360f7308b092631b1446e)