Main Program RFEM or RSTAB
Recommended Add-on Products for Timber Structures
Multilayer Surfaces such as CLT and Timber Frame Walls
The "Multilayer Surfaces" add-on for RFEM 6 optimizes the modeling and analysis of multilayer timber structures, ideal for cross-laminated timber and timber stud walls. It effectively supports the structural analysis of prefabricated timber panels.
Hybrid Timber Construction with Complementary Materials
The "Building Model" add-on simplifies the modeling and analysis of timber buildings. It speeds up the creation of building models and automatizes the load generation, ideal for demanding structural timber projects.
Construction Stages
The Construction Stages Analysis (CSA) add-on allows for considering the construction process of structures (member, surface, and solid structures) in RFEM.
Optimization of Model Parameters
The add-on uses particle swarm optimization (PSO) to determine optimal parameters for parameterized models based on weight, cost, or CO2 emissions.
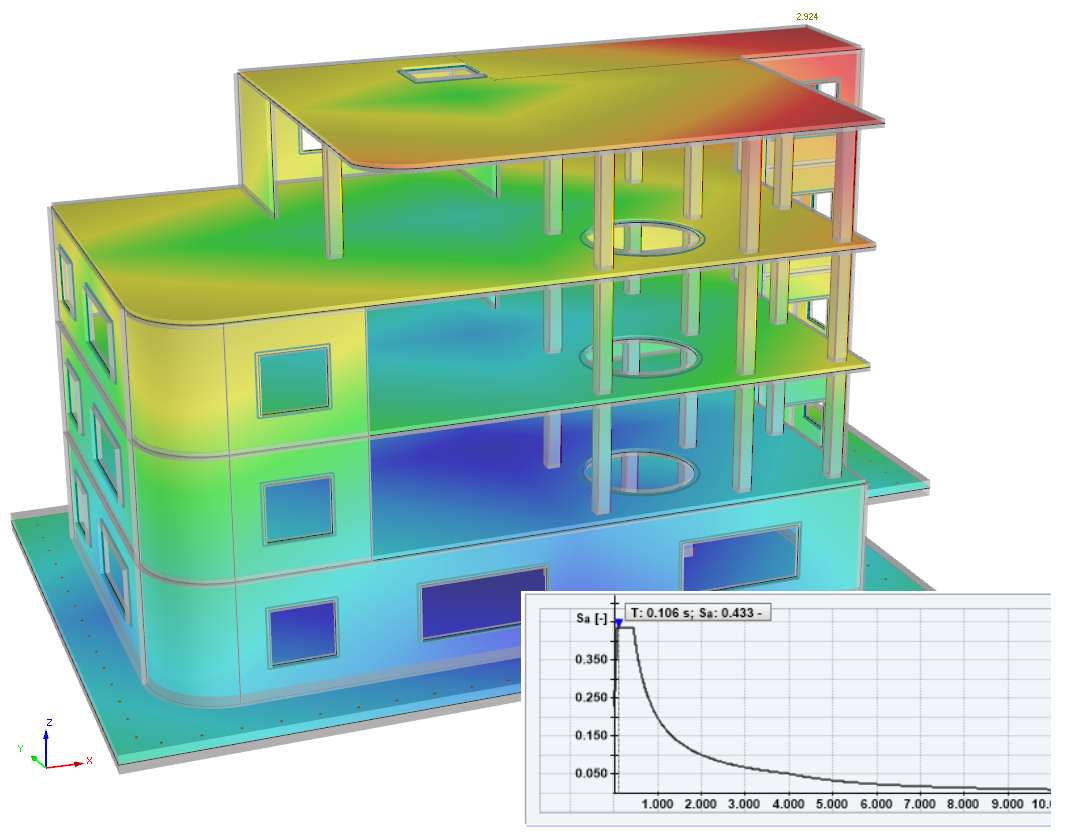
Response Spectrum Analysis
The Response Spectrum Analysis add-on performs seismic analysis using multi-modal response spectrum analysis. The spectra required for this can be created in compliance with the standards or can be user-defined. The equivalent static forces are generated from them. The add-on includes an extensive library of accelerograms from seismic zones that can be used to generate the response spectra.
Support and Learning
We provide professional support and many services in order to help you with finding a quick and efficient solution for your projects.
Integrated Standards for Timber Design
Standards for Timber Design
Annexes for EN 1995-1-1
Technical Support | Sales Team
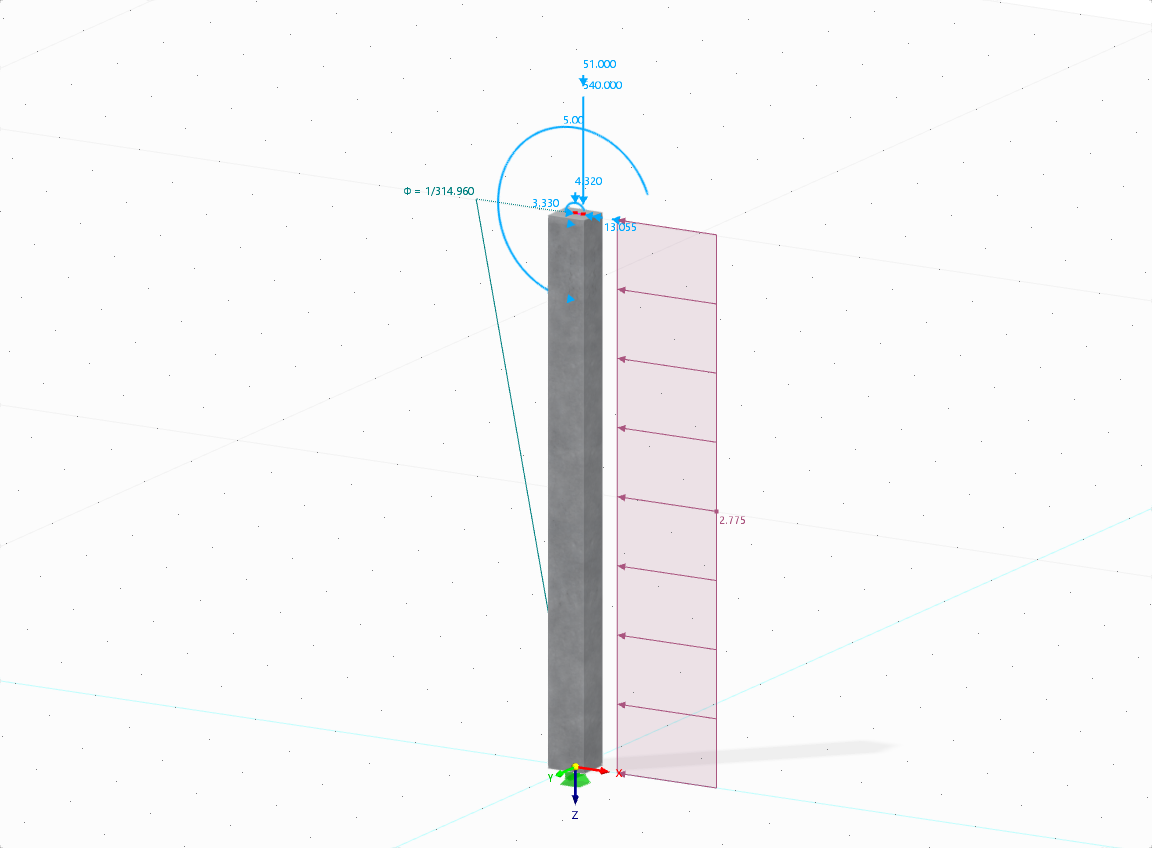
The aim of this technical article is to perform a design according to the general design method of Eurocode 2, using the example of a slender reinforced concrete column.
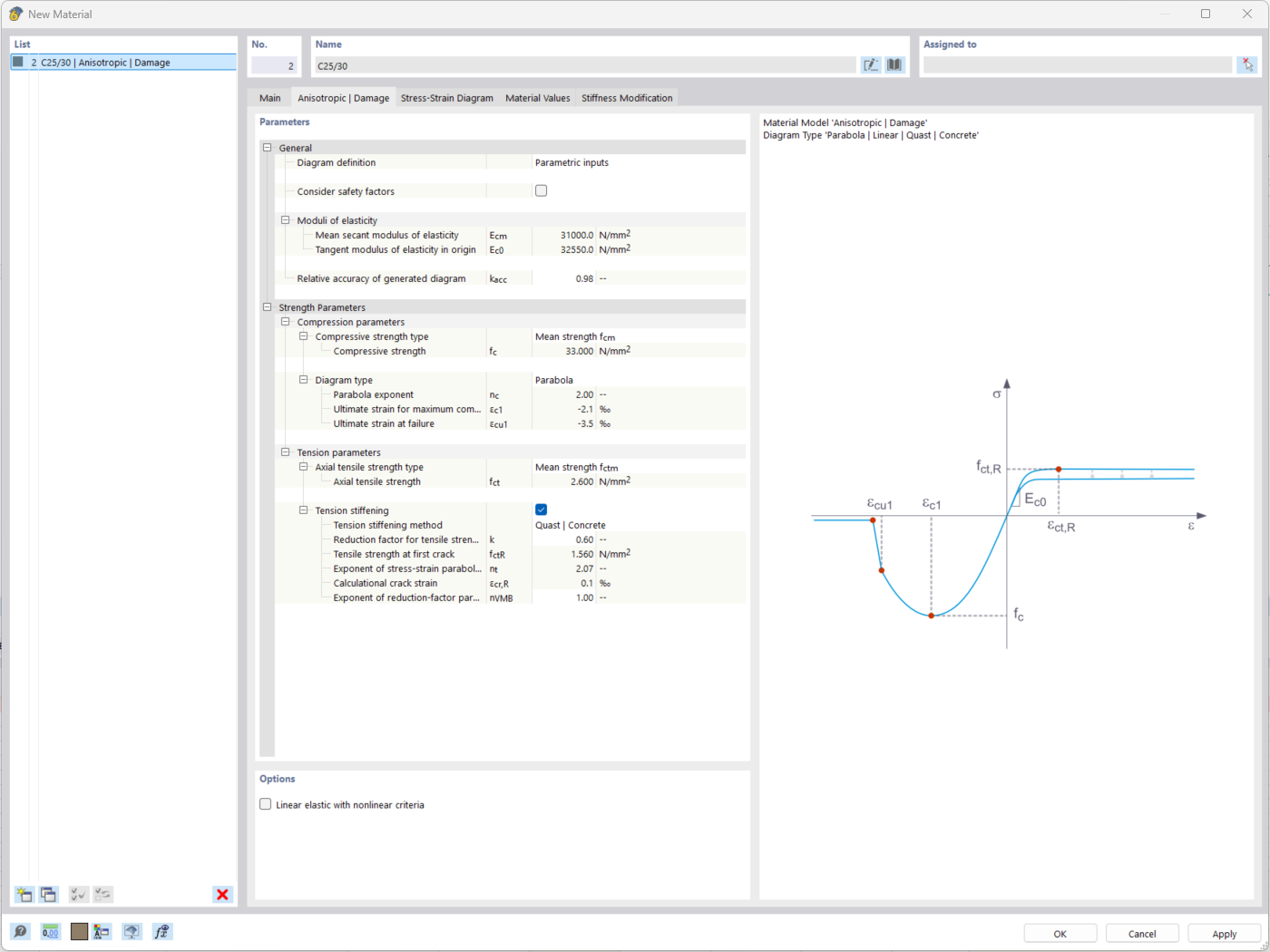
The "Nonlinear Material Behavior" add-on includes the Anistropic | Damage material model for concrete structural components. This material model allows you to consider concrete damage for members, surfaces, and solids.
You can define an individual stress-strain diagram via a table, use the parametric input to generate the stress-strain diagram, or use the predefined parameters from the standards. Furthermore, it is possible to consider the tension stiffening effect.
For the reinforcement, both nonlinear material models "Isotropic | Plastic (Members)" and "Isotropic | Nonlinear Elastic (Members)" are available.
It is possible to consider the long-term effects due to creep and shrinkage using the "Static Analysis | Creep & Shrinkage (Linear)" analysis type that has been recently released. Creep is taken into account by stretching the stress-strain diagram of the concrete using the factor (1+phi), and shrinkage is taken into account as the pre-strain of the concrete. More detailed time step analyses are possible using the "Time-Dependent Analysis (TDA)" add-on.
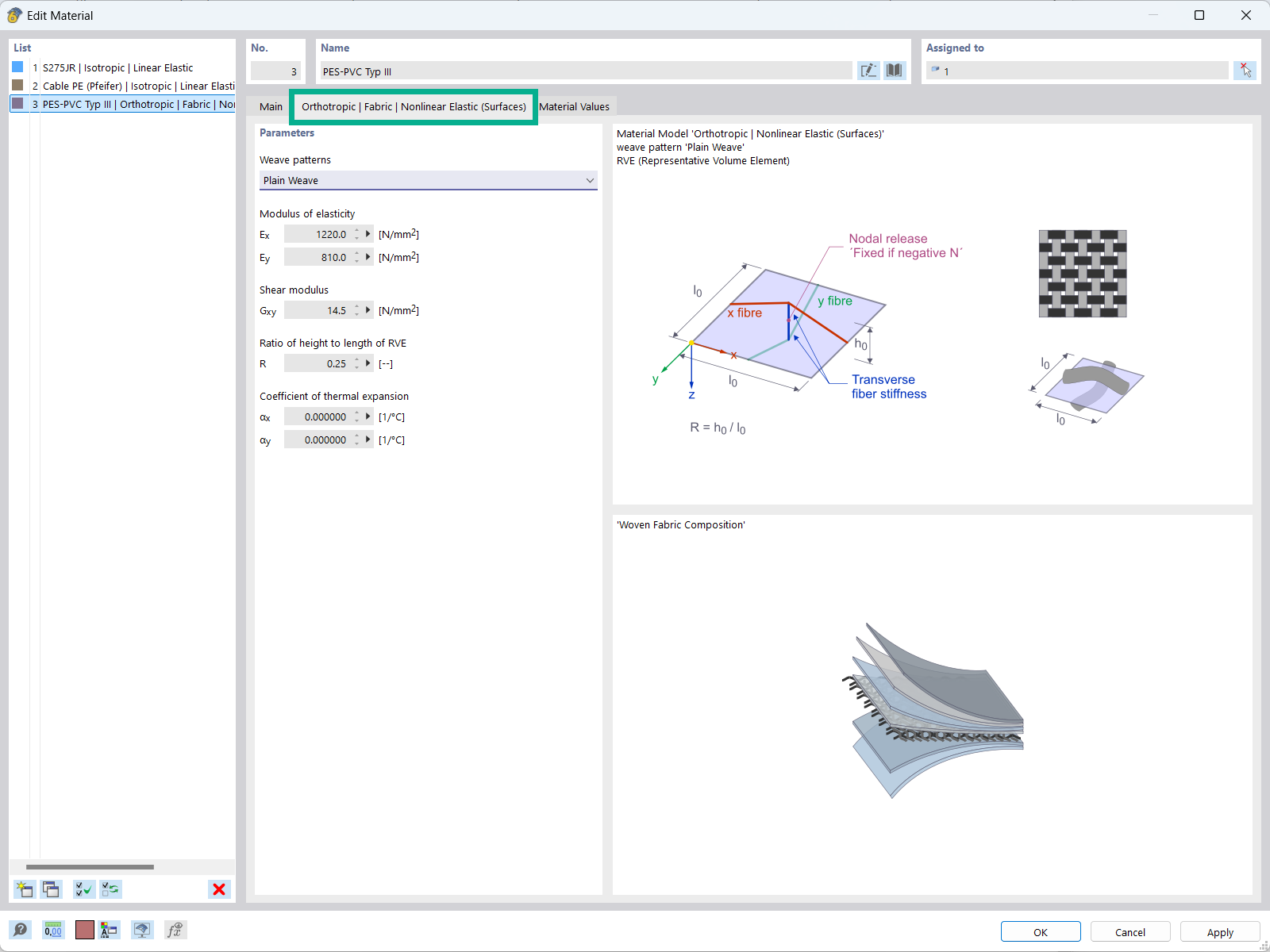
The "Orthotropic | Fabric | Nonlinear Elastic (Surfaces)" material model allows you to define prestressed fabric membranes using the representative microstructure-solid element model – RVE.
By considering the fabric geometry in the microstructure model, the corresponding transversal strain effect can now be considered for all force conditions in the membrane.
.png?mw=512&hash=57a05dc9f33b1949836c96669cadcdc6332b64e5)
Are you familiar with the Tsai-Wu material model? It combines plastic and orthotropic properties, which allows for special modeling of materials with anisotropic characteristics, such as fiber-reinforced plastics or timber.
If the material is plastified, the stresses remain constant. The redistribution is carried out according to the stiffnesses available in the individual directions. The elastic area corresponds to the Orthotropic | Linear Elastic (Solids) material model. For the plastic area, the yielding according to Tsai-Wu applies:
All strengths are defined positively. You can imagine the stress criterion as an elliptical surface within a six-dimensional space of stresses. If one of the three stress components is applied as a constant value, the surface can be projected onto a three-dimensional stress space.
If the value for fy(σ), according to the Tsai-Wu equation, plane stress condition, is smaller than 1, the stresses are in the elastic zone. The plastic area is reached as soon as fy (σ) = 1; values greater than 1 are not allowed. The model behavior is ideal-plastic, which means there is no stiffening.

Did you know? In contrast to other material models, the stress-strain diagram for this material model is not antimetric to the origin. You can use this material model to simulate the behavior of steel fiber-reinforced concrete, for example. Further information about modeling steel fiber-reinforced concrete can be found in this technical article: KB | Determining Material Properties of Steel Fiber-Reinforced Concrete and Their Application in RFEM
In this material model, the isotropic stiffness is reduced with a scalar damage parameter. This damage parameter is determined from the stress curve defined in the Diagram. This does not take the direction of the principal stresses into account; rather, the damage occurs in the direction of the equivalent strain, which also covers the third direction perpendicular to the plane. The tension and compression areas of the stress tensor are treated separately. In this case, different damage parameters apply.
The "Reference element size" controls how the strain in the crack area is scaled to the length of the element. With the default value zero, no scaling is performed. Thus, the material behavior of the steel fiber-reinforced concrete is modeled realistically.
You can find the background information on the "Isotropic Damage" material model in this technical article: KB 001461 │ Nonlinear Material Model Damage .















.png?mw=192&hash=f63e4a3f1836233005de32f60201d5392e507cf1)



.png?mw=80&hash=24e105a767cf2e175614b729c2d2fa1673e4e81b)

















