1877x

Hedi Boukraa，B.Sc.

2024-02-28

VE 1025 | 锥形悬臂梁的两跨连续梁的钢筋混凝土设计

说明

本例题中的钢筋混凝土梁为两跨悬臂梁。截面沿悬臂长度方向不断变化（变截面）。计算内力，承载能力极限状态下所需的纵向和剪切钢筋，并与 [1] 中的结果进行比较。

材料	混凝土C25/30	弹性模量	E	31000	N/mm²
	混凝土C25/30	混凝土抗压强度设计值	_fCD	14.167	N/mm²
	钢筋B500S(B)	屈服强度标准值	f_·yk	500.000	N/mm²
	钢筋B500S(B)	屈服强度设计值	f_yd	434.783	N/mm²
几何尺寸	结构	悬臂梁长度	l_eff,悬臂	4.000	m
		跨度 1 长度	l_eff,1	8.000	m
		跨度 2 长度	l_eff,2	8.000	m
	截面	高度	h	1500	毫米
		宽度	b	2620	毫米
		翼缘高度	f >h	150	毫米
		腹板宽度	_bw	380	毫米
		混凝土保护层	c_名义上	35	毫米
荷载	永久荷载	LC1	g_k,1	10.500 - 90.000 (梯形)	kN/m
		LC2	G_k,2	216.000	kN
		LC3	G_k,3	416.000	kN
	活荷载	LC4	q_k,1,1	40.000	kN/m
		LC5	q_k,1,2	40.000	kN/m
		LC6	q_k,1,3	30.000	kN/m
		LC7	Q_k,2	284.000	kN

验算示例 1025 | 永久和可变荷载

572x

42x

VE 1025 | 两跨悬臂梁

RFEM 设置

考虑支座弯矩acc的有限的弯矩重分布。简化为 5.5
整体支座端部弯矩折减或者弯矩尺寸标注参照5.3.2.2
支座边缘和距离 d 处剪力的折减到 6.2.1(8)
所使用的截面分布类型为杆件始端变截面，以考虑截面高度的变化。

结果

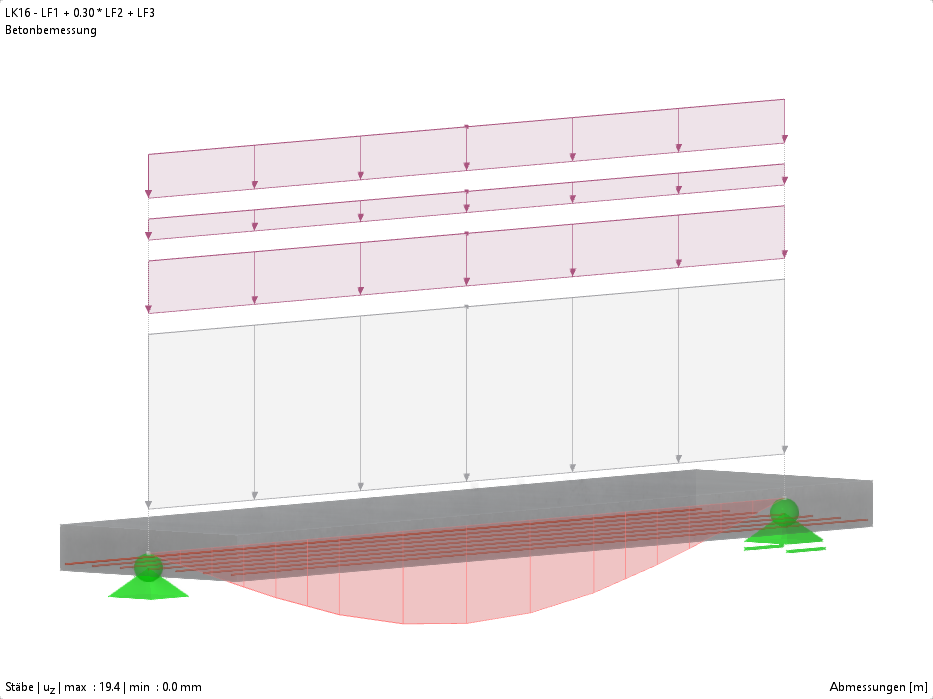
来自永久和活荷载的弯矩和剪力

有限元 g_k,1弯矩和剪力
内力	单位	RFEM/解析解	跨度 1	跨度 2	A 轴	B 轴	C 轴
弯矩	[kNm]	RFEM	248.890	432.840	-296.460	-645.760	0
弯矩	[kNm]	分析解决方案	249.000	433.000	-296.000	-646.000	0
剪力	[kN]	RFEM	-43.330	80.830	-201.000/316.340	-403.660/440.720	-279.280
剪力	[kN]	分析解决方案	-44.000	81.000	-201.000/316.000	-404.000/441.000	-279.000

验算示例 1025 | 荷载工况 LC1 的弯矩和剪力

作用G_k,2作用下的弯矩和剪力
内力	单位	RFEM/解析解	跨度 1	跨度 2	A 轴	B 轴	C 轴
弯矩	[kNm]	RFEM	-305.850	101.850	-815.400	203.720	0
弯矩	[kNm]	分析解决方案	-306.000	102.000	-815.000	204.000	0
剪力	[kN]	RFEM	127.390	-25.460	-215.670/127.390	-127.390/-25.460	-25.460
剪力	[kN]	分析解决方案	127.000	-25.500	-216.000/127.000	-127.000/-25.500	-25.500

验算示例 1025 | 荷载工况 LC2 的弯矩和剪力

作用G_k,3作用下的弯矩和剪力
内力	单位	RFEM/解析解	跨度 1	跨度 2	A 轴	B 轴	C 轴
弯矩	[kNm]	RFEM	676.040	-155.960	0	-311.920	0
弯矩	[kNm]	分析解决方案	626.000	156.000	0	-312.000	0
剪力	[kN]	RFEM	169.010/-246.990	-38.990	169.010	-246.990/38.990	38.990
剪力	[kN]	分析解决方案	169.000/247.000	39.000	169.000	-247.000/39.000	39.000

验算示例 1025 | 荷载工况 LC3 的弯矩和剪力

由 q 引起的弯矩和剪力_k,1,1
内力	单位	RFEM/解析解	跨度 1	跨度 2	A 轴	B 轴	C 轴
弯矩	[kNm]	RFEM	-120.100	40.000	-320.200	79.950	0
弯矩	[kNm]	分析解决方案	-120.220	40.030	-320.490	80.060	0
剪力	[kN]	RFEM	50.070	-10.000	-160.000/50.020	50.020/-10.000	-10.000
剪力	[kN]	分析解决方案	50.000	-10.010	-160.000/50.070	50.070/-10010	-10.010

验算示例 1025 | 荷载工况LC4的弯矩和剪力

由q引起的弯矩和剪力_k,1,2
内力	单位	RFEM/解析解	跨度 1	跨度 2	A 轴	B 轴	C 轴
弯矩	[kNm]	RFEM	240.020	-79.980	0	-159.960	0
弯矩	[kNm]	分析解决方案	240.000	-80.000	0	-160.000	0
剪力	[kN]	RFEM	-19.990	19.990	140.010	-179.990/19.999	19.999
剪力	[kN]	分析解决方案	-20.000	20.000	140.000	-180.000/20.000	20.000

验算示例 1025 | 荷载工况 LC5 的弯矩和剪力

由 q 引起的弯矩和剪力_k,1,3
内力	单位	RFEM/解析解	跨度 1	跨度 2	A 轴	B 轴	C 轴
弯矩	[kNm]	RFEM	-59.980	180.010	0	-119.970	0
弯矩	[kNm]	分析解决方案	-60.000	184.000	0	-120.000	0
剪力	[kN]	RFEM	-15.000	15.000	-15.000	-15000/135000	-105.000
剪力	[kN]	分析解决方案	-15.000	15.000	-15.000	-15000/135000	-105.000

验算示例 1025 | 荷载工况 LC6 的弯矩和剪力

不当弯矩和剪力 Q_k,2
内力	单位	RFEM/解析解	跨度 1	跨度 2	A 轴	B 轴	C 轴
弯矩	[kNm]	RFEM	461.530	-106.470	0	-212.950	0
弯矩	[kNm]	分析解决方案	462.000	-106.500	0	-213.000	0
剪力	[kN]	RFEM	115.380/-168.620	26.620	115.380	-1680.000/26.620	26.620
剪力	[kN]	分析解决方案	-169,000/115,000	26.600	115.000	-15000/135000	-169.000/26.600

验算示例 1025 | 荷载工况LC7的弯矩和剪力

内力

下表列出了承载能力极限状态下的所有荷载组合：

荷载组合	分配的荷载工况
二氧化碳1	1.00·LC1 + 1.00·LC2 + 1.00·LC3
CO2	1.35·LC1 + 1.35·LC2 + 1.35·LC3 + 1.50·LC4 + 1.50·LC5 + 1.50·LC6 + (1.50·LC7)
CO3	1.35·LC1 + 1.35·LC2 + 1.35·LC3 + (1.50·0.70)·LC4 + (1.50·0.70)·LC5 + (1.50·0.70)·LC6 + 1.50·LC7
CO4	1.35·LC1 + 1.00·LC2 + 1.35·LC3 + 1.50·LC5 + 1.50·LC6 + (1.50·LC6) + (1.50·LC7)
CO5	1.35·LC1 + 1.00·LC2 + 1.35·LC3 + (1.50·0.70)·LC5 + 1.50·LC7
CO6	1.00·LC1 + 1.35·LC2 + 1.35·LC3 + (1.50·0.70)·LC4 + 1.50·LC7
CO7	1.35·LC1 + 1.00·LC2 + 1.35·LC3 + (1.50·0.70)·LC5 + (1.50·0.70)·LC6+ 1.50·LC7
CO8	1.35·LC1 + 1.35·LC2 + 1.00·LC3 + 1.50·LC4 + 1.50·LC6
CO9	1.35·LC1 + 1.35·LC2 + 1.35·LC3 + 1.50·LC4 + 1.50·LC5 + (1.50·LC7)

作用	单位	荷载组合	RFEM 结果	参考结果	比值
M_Ed,A	kNm	CO8	-1981.830	-1980.000	1.00
M_Ed,B	kNm	CO4	-1764.600	-1765.000	0.99
M_Ed,1	kNm	CO5	1887.120	1887.000	1.00
M_Ed,2	kNm	CO8	885.540	895.000	0.99
V_Ed,A,li	kN	CO2	-802.500	-803.000	0.99
V_Ed,A,re	kN	CO9	1250.770	1250.000	1.00
V_Ed,1,li	kN	CO6	582.090	581.000	1.00
V_Ed,1,re	kN	CO7	-554.660	-555.000	0.99
V_Ed,B,li	kN	CO4	-1245.820	-1246.000	0.99
V_Ed,B,re	kN	CO4	-886.580	-887.000	0.99
V_Ed,C	kN	CO8	-544.930	-545.000	0.99

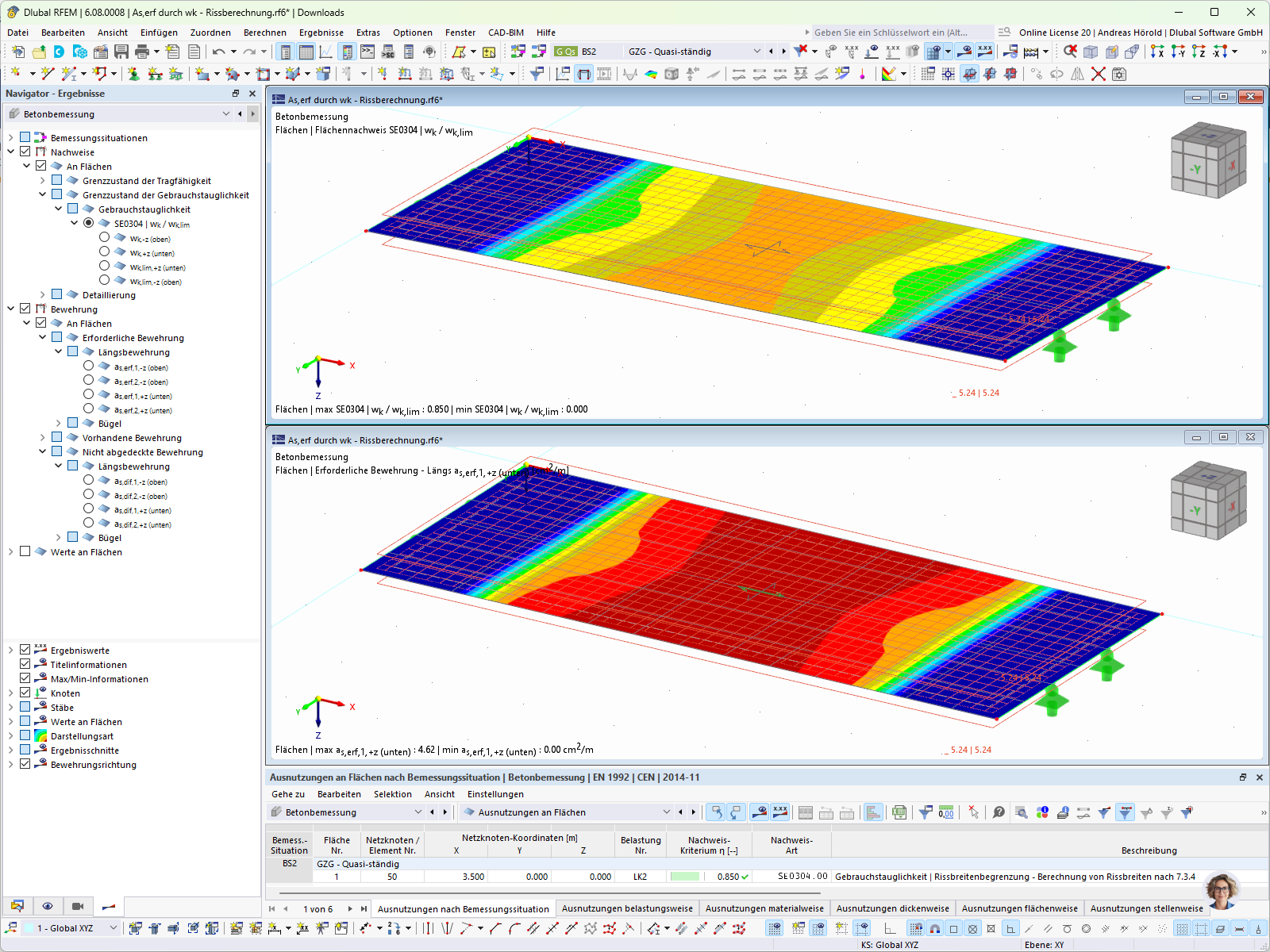
==== 需配的纵向配筋 ====
文献中在荷载组合 4 中和支座 B 7 处考虑了 12% 的弯矩重分布，相比之下，RFEM 对所有荷载组合采用相同的弯矩重分布方法。为了与文献中的文献进行比较，需要对 RFEM 模型进行调整。
'''RFEM与文献比较：'''
'''支座 A：'''位于支座面上。然而，该文献在计算支座端部弯矩时忽略了荷载的影响。为了能够与 RFEM 中的结果进行有意义的比较，有必要在考虑荷载影响的情况下重新计算。不考虑荷载影响的情况下，支座边缘的设计弯矩 M_Ed为 -kNm。考虑荷载的影响，M_Ed增加到-1823.0 kNm。

	RFEM软件		解析解		比值
荷载工况	弯矩设计值 M_Ed	需配的钢筋 A_s,stat,tot	弯矩设计值 M_Ed	需配的钢筋 A_s,stat,tot	M_Ed	A_s,stat,tot
	[kNm]	[厘米² ]	[kNm]	[厘米² ]	[kNm]	[厘米² ]
CO8	-1824.790	32.50	-1823.000	31.60	1.00	1.02

In the literature, it is assumed that the cross-section height at the edge of the support is equal to the cross-section height at the middle of the support. RFEM 程序会自动考虑变截面的实际截面高度。因此，这在 RFEM 中提出了更高的配筋要求。
'''支座 B：'''
这种情况下的临界荷载组合是荷载组合 4。为了与文献相符，支座 B 的弯矩重分配比设为 0.850。

支座B
	RFEM软件		解析解		比值
荷载工况	弯矩设计值 M_Ed	需配的钢筋 A_s,stat,tot	弯矩设计值 M_Ed	需配的钢筋 A_s,stat,tot	M_Ed	A_s,stat,tot
	[kNm]	[厘米² ]	[kNm]	[厘米² ]	[kNm]	[厘米² ]
CO4	-1345.870	22.40	-1360.000	22.80	0.99	0.98

When calculating the design moment, the literature takes into consideration that the moment at the face of the support should not be less than 0.65 of the full fixed end moment (DIN EN 1992-1-1, 5.3.2.2). 该条件在 RFEM 中不适用。
'''跨度 1:'''
由于在 RFEM 中梁被定义为连续杆件，因此无法为每个跨度都指定一个有效宽度 b_eff 。选择跨 1 和 2 的两个有效宽度中的最小值来简化。 b_eff设为 2.620 m。文献考虑荷载组合 7 的弯矩分配率为 12%，因此中间支座的弯矩分配率为 0.880。

跨度 1
	RFEM软件		解析解		比值
荷载工况	弯矩设计值 M_Ed	需配的钢筋 A_s,stat,tot	弯矩设计值 M_Ed	需配的钢筋 A_s,stat,tot	M_Ed	A_s,stat,tot
	[kNm]	[厘米² ]	[kNm]	[厘米² ]	[kNm]	[厘米² ]
CO7	1926.280	30.13	1927.000	33.10	0.99	0.91

'''Span 2:''' In this case, no moment redistribution is considered.

跨度 2
	RFEM软件		解析解		比值
荷载工况	弯矩设计值 M_Ed	需配的钢筋 A_s,stat,tot	弯矩设计值 M_Ed	需配的钢筋 A_s,stat,tot	M_Ed	A_s,stat,tot
	[kNm]	[厘米² ]	[kNm]	[厘米² ]	[kNm]	[厘米² ]
CO8	885.520	13.79	895.000	15.10	0.99	0.91

In the literature, the required longitudinal reinforcement is determined using approximation methods for T-beams according to DAstb-heft 425. 此处假定翼缘处的压力位于翼缘的中心 (h_f/2) 上。在 RFEM 中所需的钢筋截面可以通过截面分析来确定。这导致所需的配筋率比文献中的要低。
'''RFEM 提供的解决方案'''
现在将中间支座的弯矩重分布率为所有荷载组合的 15%。计算结果总结在下表中。
'''支座 A：'''
荷载工况 8 传递的弯矩最大，因此起决定性作用。

支座 A
荷载工况	弯矩设计值 M_Ed	需配的钢筋 A_s,stat,tot
	[kNm]	[厘米² ]
CO8	-1824.840	32.32

'''Support B:'''

支座B：
荷载工况	弯矩设计值 M_Ed	需配的钢筋 A_s,stat,tot
	[kNm]	[厘米² ]
CO4	-1345.890	22.40

'''Span 1:''' When moment redistribution is taken into consideration in all load combinations, CO5 has the highest design bending moment in Span 1.

跨度 1：
荷载工况	弯矩设计值 M_Ed	需配的钢筋 A_s,stat,tot
	[kNm]	[厘米² ]
CO5	2005.410	31.44

'''Span 2:''' CO8 has a design moment after moment redistibution M_Ed of 940 kNm.

跨度 2：
荷载工况	弯矩设计值 M_Ed	需配的钢筋 A_s,stat,tot
	[kNm]	[厘米² ]
CO8	940.000	14.73

验算示例 1025 | 实配和需求的纵向配筋

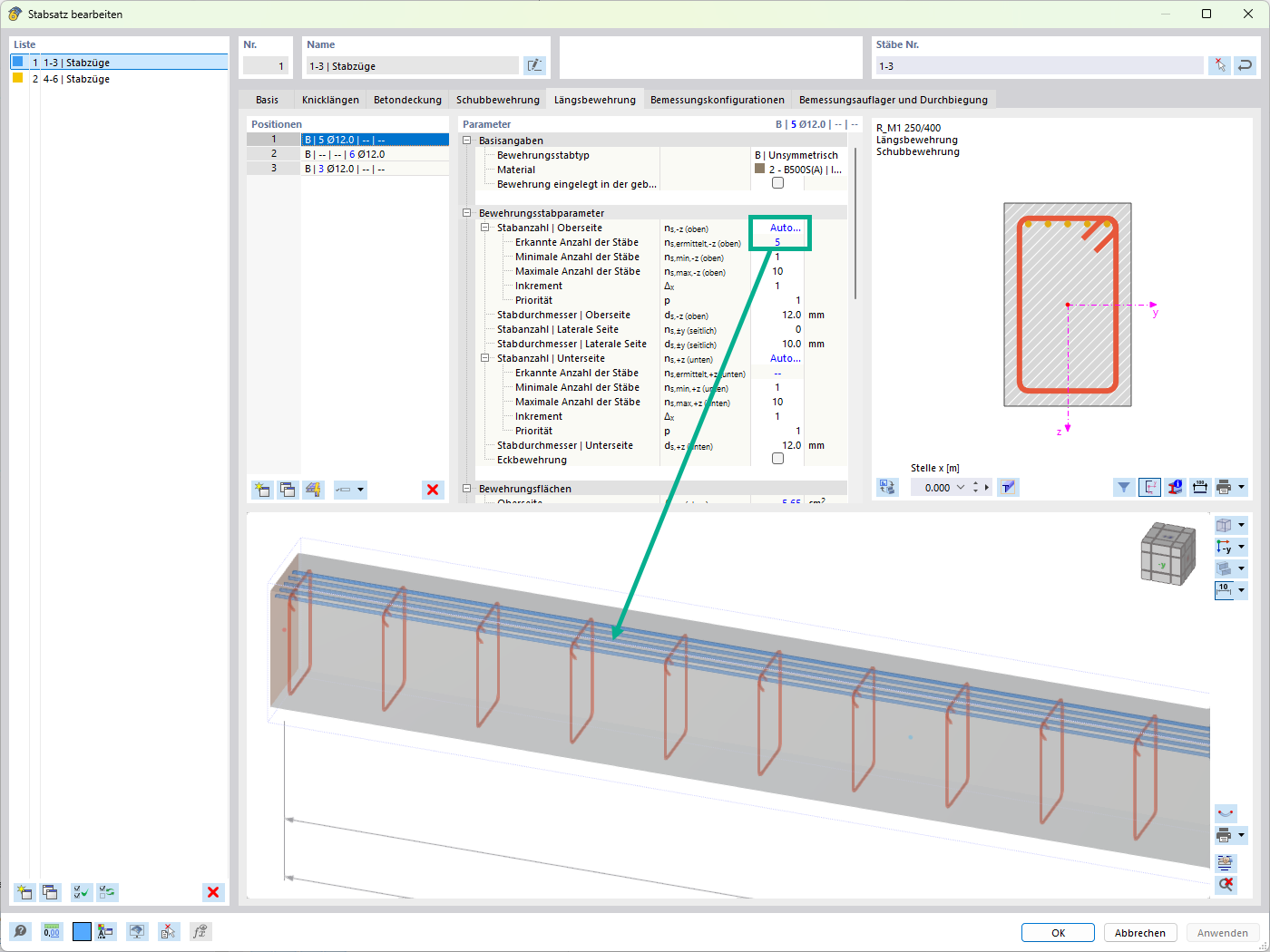
==== 抗剪配筋 ====
'''悬臂梁上的抗剪配筋：'''
为了确定悬臂梁上所需的箍筋，总共检查了 3 个位置。计算结果汇总于下表中：

悬臂
位置 x	参数	符号	单位	RFEM软件	解析解	比值
x = 0.45m	有效高度	d	[m]	0.940	0.920	1.02
	内力臂	[SCHOOL.ZIP]	[m]	0.848	0.828	1.02
	剪力	V_Ed	[kN]	-327.190	-328.000	0.99
	弯矩设计值	M_Ed	[kNm]	-73.320	-74.000	0.99
	受压区域内力的剪力设计值	V_ccd	[kN]	12.550	13.000	0.99
	剪力设计值	V_Ed,red	[kN]	314.640	314.000	1.0
	无钢筋抗剪承载力	V_rd,cc	[kN]	219.420	221.00	0.99
	斜压杆的倾角	ct θ	[-]	3.0	3.0	1.0
	斜压杆承载力	V_rd,max	[kN]	996.230	1003.000	0.99
	所需配筋	a_sw,req	[厘米²/米]	2.84	2.91	0.98
x = 1.37 m	有效高度	d	[m]	1.070	1.050	1.02
	内力臂	[SCHOOL.ZIP]	[m]	0.965	0.945	1.02
	剪力	V_Ed	[kN]	-417.720	-418.000	1.00
	弯矩设计值	M_Ed	[kNm]	-414.250	-415.000	1.00
	受压区域内力的剪力设计值	V_ccd	[kN]	62.210	66.000	0.94
	剪力设计值	V_Ed,red	[kN]	355.510	353.000	1.01
	无钢筋抗剪承载力	V_rd,cc	[kN]	250.070	252.000	0.99
	斜压杆的倾角	ct θ	[-]	3.0	3.0	1.0
	斜压杆承载力	V_rd,max	[kN]	1135.860	1144.000	0.99
	所需配筋	a_sw,req	[厘米²/米]	2.83	2.86	0.99
x = 2.37 m	有效高度	d	[m]	1.210	1.190	1.02
	内力臂	[SCHOOL.ZIP]	[m]	1.090	1.070	1.02
	剪力	V_Ed	[kN]	-541.800	-543.000	1.0
	弯矩设计值	M_Ed	[kNm]	-891.790	-893.00	1.00
	受压区域内力的剪力设计值	V_ccd	[kN]	118.250	125.000	0.95
	剪力设计值	V_Ed,red	[kN]	423.550	418.000	1.01
	无钢筋抗剪承载力	V_rd,cc	[kN]	283.220	285.000	0.99
	斜压杆的倾角	ct θ	[-]	3.0	3.0	1.0
	斜压杆承载力	V_rd,max	[kN]	1286.410	1298.000	0.99
	所需配筋	a_sw,req	[厘米²/米]	2.98	2.99	1.0

'''Span 1:''' The decisive member location for the calculation of the stirrups in field 1 is at a distance d from the right edge of the support A.

跨度 1
参数	符号	单位	RFEM软件	解析解	比率
有效高度	d	[m]	1.440	1.430	1.00
支座 A 处的剪力	V_Ed,A	[kN]	1250.770	1250.000	1.00
剪力设计值	V_Ed,A,re	[kN]	952.430	954.000	1.00
无钢筋抗剪承载力	V_Rd,cc	[kN]	346.210	343.000	1.00
斜压杆的倾角	ct θ	[-]	1.88	1.87	1.00
所需抗剪配筋	a_sw,req	[厘米²/米]	8.95	9.11	0.98

'''Span 2:''' The calculation of the stirrups is done analog to span 1.

跨度 2
参数	符号	单位	RFEM软件	解析解	比率
有效高度	d	[m]	1.440	1.440	1.02
支座 B 处的剪力	V_Ed,B	[kN]	886.580	855.000	1.03
剪力设计值	V_Ed,B,re	[kN]	613.100	584.000	1.05
无钢筋抗剪承载力	V_Rd,cc	[kN]	346.210	343.000	1.00
斜压杆的倾角	ct θ	[-]	2.75	2.91	0.95
所需抗剪配筋	a_sw,req	[厘米²/米]	3.94	3.58	1.10

跨 2 的结果的差异是由于文献考虑了弯矩重分配后的支座 B 处的剪力。但是弯矩重发布并不影响 RFEM 中的剪力验算

验算示例 1025 | 已提供和需要的横向配筋

572x

42x

VE 1025 | 两跨悬臂梁

参考

德国混凝土与结构工程协会 E. V, 按欧洲规范 2 计算的实例。第 1 卷：建筑施工，柏林： Ernst & Sohn 2012, 一等奖更正了 1 的再版。版本，978-3-433-01877-4

;