Descripción del trabajo
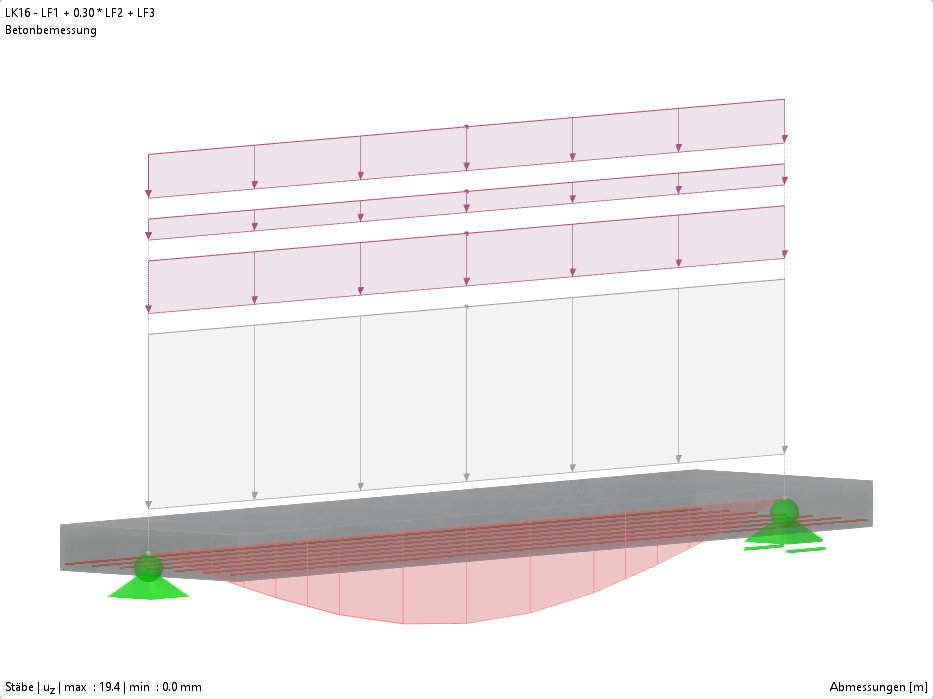
Una viga de hormigón armado se calcula como una viga de dos vanos con un voladizo. La sección varía a lo largo del voladizo (sección de sección variable). Los esfuerzos internos, la armadura longitudinal necesaria y la armadura de cortante para el estado límite último se calculan y comparan con los resultados en [1].
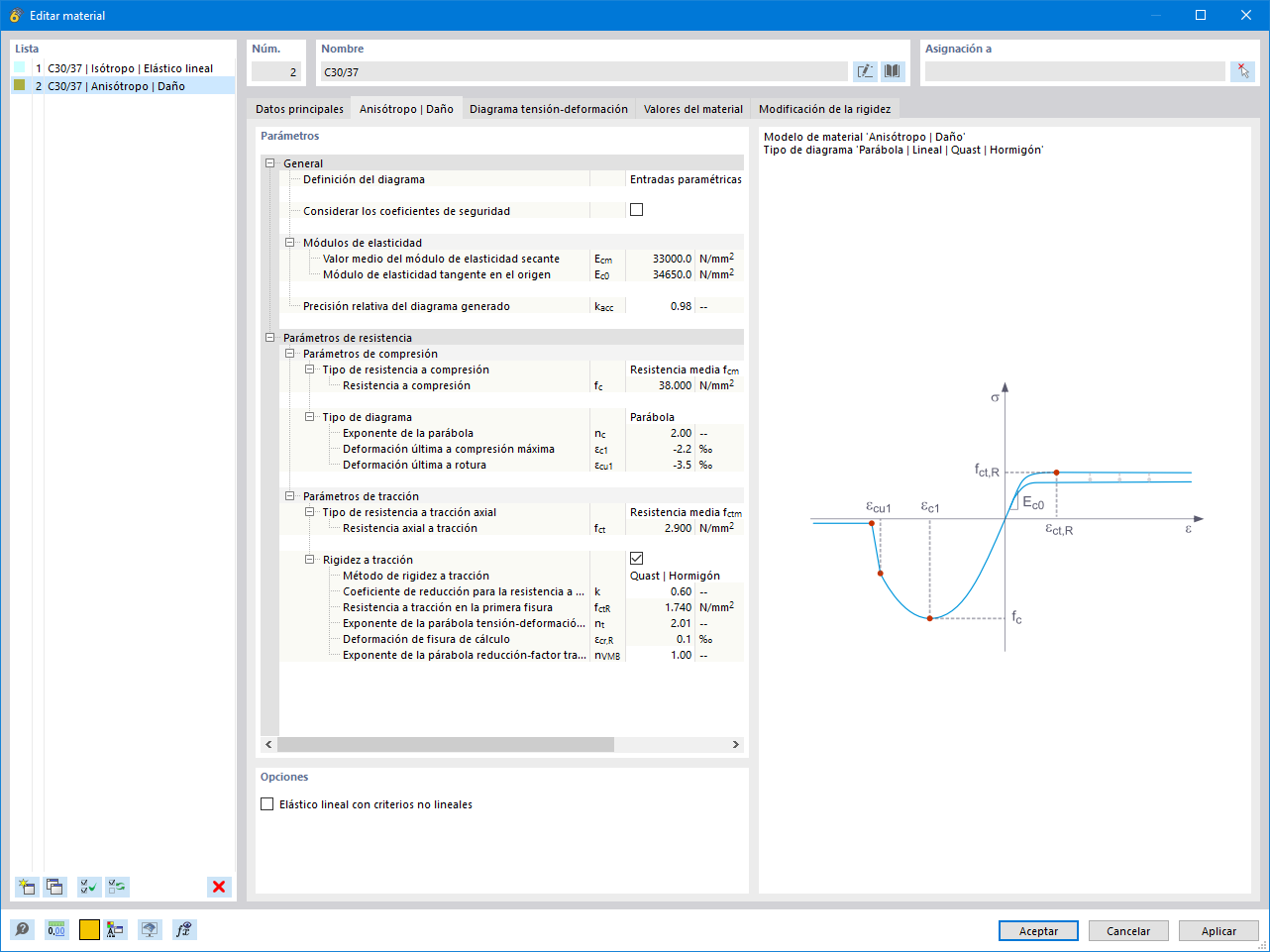
| Material | Hormigón C25/30 | Módulo de elasticidad | E | 31000 | N/mm2 |
| Valor de cálculo de la resistencia a compresión del hormigón | fcd | 14,167 | N/mm2 | ||
| Acero de armadura B500S(B) | Límite elástico característico | fyk | 500,000 | N/mm2 | |
| Límite elástico de cálculo | fyd | 434,783 | N/mm2 | ||
| Geometría | Estructura | Longitud del voladizo | leff,voladizo | 4,000 | m |
| Longitud del vano 1 | leff,1 | 8,000 | m | ||
| Longitud del vano 2 | leff,2 | 8,000 | m | ||
| Sección | Altura | H | 1500 | mm | |
| Ancho | b | 2620 | mm | ||
| Altura del ala | hf | 150 | mm | ||
| Anchura del alma | bw | 380 | mm | ||
| Recubrimiento de hormigón | cnom | 35 | mm | ||
| Cargas | Cargas permanentes | CC1 | gk,1 | 10,500 - 90,000 (trapezoidal) | kN/m |
| CC2 | Gk,2 | 216,000 | kN | ||
| CC3 | Gk,3 | 416,000 | kN | ||
| Sobrecargas de uso | CC4 | qk,1,1 | 40,000 | kN/m | |
| CC5 | qk,1,2 | 40,000 | kN/m | ||
| CC6 | qk,1,3 | 30,000 | kN/m | ||
| CC7 | Qk,2 | 284,000 | kN |
416x
23x
Configuración de RFEM
- Consideración de la redistribución limitada del momento del apoyo según hasta 5,5
- Reducción de los momentos o dimensionamiento para los momentosen la cara de un apoyo monolítico acc. hasta 5.3.2.2
- Reducción de los esfuerzos cortantes en la cara del apoyo y la distancia d según hasta 6.2.1(8)
- El tipo de distribución de la sección utilizada es de sección variable al inicio de la barra, para considerar el cambio de altura de la sección.
Resultados
- Momento flector y esfuerzo cortante a partir de cargas permanentes y de uso
Momento flector y esfuerzo cortante debido a gk,1 Esfuerzo interior Unidad RFEM/Solución analítica Vano 1 Vano 2 Eje A Eje B Eje C Momento flector [kNm] RFEM 248,890 432,840 -296.460 -645,760 0 Solución analítica 249,000 433,000 -296.000 -646.000 0 Esfuerzo cortante, [kN] RFEM -43,330 80,830 -201.000/316.340 -403.660/440.720 -279.280 Solución analítica -44 000 81,000 -201.000/316.000 -404.000/441.000 -279.000 Momento flector y esfuerzo cortante debido a Gk,2 Esfuerzo interior Unidad RFEM/Solución analítica Vano 1 Vano 2 Eje A Eje B Eje C Momento flector [kNm] RFEM -305.850 101,850 -815.400 203,720 0 Solución analítica -306.000 102,000 -815.000 204,000 0 Esfuerzo cortante, [kN] RFEM 127,390 -25.460 -215.670/127.390 -127,390/-25,460 -25.460 Solución analítica 127,000 -25.500 -216.000/127.000 -127.000/-25.500 -25.500 Momento flector y esfuerzo cortante debido a Gk,3 Esfuerzo interior Unidad RFEM/Solución analítica Vano 1 Vano 2 Eje A Eje B Eje C Momento flector [kNm] RFEM 676,040 -155,960 0 -311,920 0 Solución analítica 676,000 156,000 0 -312.000 0 Esfuerzo cortante, [kN] RFEM 169.010/-246.990 -38,990 169,010 -246.990/38.990 38,990 Solución analítica 169.000/247.000 39,000 169,000 -247.000/39.000 39,000 Momento flector y esfuerzo cortante debido a qk,1,1 Esfuerzo interior Unidad RFEM/Solución analítica Vano 1 Vano 2 Eje A Eje B Eje C Momento flector [kNm] RFEM -120.100 40,000 -320.200 79,950 0 Solución analítica -120,220 40,030 -320.490 80,060 0 Esfuerzo cortante, [kN] RFEM 50,070 -10.000 -160.000/50.020 50,020/-10,000 -10.000 Solución analítica 50,000 -10.010 -160.000/50.070 50,070/-10,010 -10.010 Momento flector y esfuerzo cortante debido a qk,1,2 Esfuerzo interior Unidad RFEM/Solución analítica Vano 1 Vano 2 Eje A Eje B Eje C Momento flector [kNm] RFEM 240,020 -79,980 0 -159,960 0 Solución analítica 240,000 -80.000 0 -160.000 0 Esfuerzo cortante, [kN] RFEM -19,990 19,990 140,010 -179,990/19,999 19,999 Solución analítica -20.000 20,000 140,000 -180.000/20.000 20,000 Momento flector y esfuerzo cortante debido a qk,1,3 Esfuerzo interior Unidad RFEM/Solución analítica Vano 1 Vano 2 Eje A Eje B Eje C Momento flector [kNm] RFEM -59,980 180,010 0 -119,970 0 Solución analítica -60.000 184,000 0 -120.000 0 Esfuerzo cortante, [kN] RFEM -15 000 15,000 -15 000 -15.000/135.000 -105.000 Solución analítica -15 000 15,000 -15 000 -15.000/135.000 -105.000 Momento flector y esfuerzo cortante debido a Qk,2 Esfuerzo interior Unidad RFEM/Solución analítica Vano 1 Vano 2 Eje A Eje B Eje C Momento flector [kNm] RFEM 461,530 -106,470 0 -212,950 0 Solución analítica 462,000 -106.500 0 -213.000 0 Esfuerzo cortante, [kN] RFEM 115,380/-168,620 26,620 115,380 -168.620/26.620 26,620 Solución analítica -169.000/115.000 26,600 115,000 -15.000/135.000 -169.000/26.600
- Esfuerzos internos
La siguiente tabla contiene todas las combinaciones de carga del estado límite último:Combinación de cargas Casos de carga asignados CO1 1,00·CC1 + 1,00·CC2 + 1,00·CC3 CO2 1,35·CC1 + 1,35·CC2 + 1,35·CC3 + 1,50·CC4 + 1,50·CC5 + 1,50·CC6 + (1,50·0,80)·CC7 CO3 1,35·CC1 + 1,35·CC2 + 1,35·CC3 + (1,50·0,70)·CC4 + (1,50·0,70)·CC5 + (1,50·0,70)·CC6 + 1,50·CC7 CO4 1,35·CC1 + 1,00·CC2 + 1,35·CC3 + 1,50·CC5 + 1,50·CC6 + (1,50·0,80)·CC7 CO5 1,35·CC1 + 1,00·CC2 + 1,35·CC3 + (1,50·0,70)·CC5 + 1,50·CC7 CO6 1,00·CC1 + 1,35·CC2 + 1,35·CC3 + (1,50·0,70)·CC4 + 1,50·CC7 CO7 1,35·CC1 + 1,00·CC2 + 1,35·CC3 + (1,50·0,70)·CC5 + (1,50·0,70)·CC6+ 1,50·CC7 CO8 1,35·CC1 + 1,35·CC2 + 1,00·CC3 + 1,50·CC4 + 1,50·CC6 CO9 1,35·CC1 + 1,35·CC2 + 1,35·CC3 + 1,50·CC4 + 1,50·CC5 + (1,50·0,80)·CC7
Acción Unidad Combinación de carga Resultado de RFEM Resultado de referencia Razón MEd,A kNm CO8 -1981.830 -1980.000 1.00 MEd,B kNm CO4 -1764.600 -1765.000 0,99 Med,1 kNm CO5 1887,120 1887,000 1.00 Ed,2 kNm CO8 885,540 895,000 0,99 VEd,A,li kN CO2 -802.500 -803.000 0,99 VEd,A,re kN CO9 1250,770 1250,000 1.00 VEd,1,li kN CO6 582,090 581,000 1.00 VEd,1,re kN CO7 -554.660 -555.000 0,99 VEd,B,li kN CO4 -1245.820 -1246.000 0,99 VEd,B,re kN CO4 -886.580 -887.000 0,99 VEd,C kN CO8 -544.930 -545.000 0,99 En la literatura, se consideró una redistribución del momento del 15% en el apoyo B dentro de las combinaciones de carga 4, y una redistribución del momento del 12% dentro de la combinación de carga 7. Por el contrario, RFEM aplica la misma redistribución de momentos en todas las combinaciones de carga. Para facilitar una comparación significativa con la literatura, se realizarán ajustes en el modelo de RFEM. Posteriormente, se presentará la solución real proporcionada por '''RFEM''' '''.''' está en la cara del apoyo. Sin embargo, la bibliografía omite la influencia de la carga al calcular el momento en la cara del apoyo. Para permitir una comparación significativa con los resultados en RFEM, es necesario volver a calcularlo considerando la influencia de la carga. El momento de cálculo en la cara del apoyo sin consideración de influencia de carga, MEd, es - 1819,0 kNm. Considerando el efecto de las cargas, MEd aumenta a- 1823,0 kNm.
{>class="table-header"RFEM Solución analítica Razón Caso de carga Momento flector de cálculo MEd Armadura necesaria As,stat,tot Momento flector de cálculo MEd Armadura necesaria As,stat,tot MED As,stat,tot [kNm] [cm2 ] [kNm] [cm2 ] [kNm] [cm2 ] CO8 -1824.790 32,50 -1823.000 31,60 1.00 1,02
En la literatura, se supone que la altura de la sección en el borde del apoyo es igual a la altura de la sección en el medio del apoyo. Sin embargo, en RFEM, se considera la altura real de la sección debido a la sección de sección variable. Como resultado, esto conduce a mayores requisitos de armadura en RFEM.
'''Apoyo B:'''
La combinación de carga crítica en este caso es la combinación de carga 4. Para coincidir con la bibliografía, la relación de redistribución de momentos en el apoyo B se establece en 0,850.
Apoyo B RFEM Solución analítica Razón Caso de carga Momento flector de cálculo MEd Armadura necesaria As,stat,tot Momento flector de cálculo MEd Armadura necesaria As,stat,tot MEd As,stat,tot [kNm] [cm2 ] [kNm] [cm2 ] [kNm] [cm2 ] CO4 -1345.870 22,40 -1360.000 22,80 0,99 0.98
Al calcular el momento de cálculo, la bibliografía tiene en cuenta que el momento en la cara del apoyo no debe ser menor que 0.65 del momento fijo total en el extremo (DIN EN 1992-1-1, 5.3.2.2). Esta condición no está implementada en RFEM. Esto explica la diferencia en el momento de cálculo. '''Vano 1:'''
Dado que la viga se define como una barra continua en RFEM, no es posible establecer una anchura eficazbeff para cada vano. El valor más pequeño de las dos anchuras eficaces del vano 1 y 2 se usa para simplificar. beff se establece en 2,620 m. La bibliografía considera una redistribución de momentos del 12 % para la combinación de carga 7, por lo que la relación de redistribución de momentos en el apoyo central ahora se establece en 0,880.
Vano 1 RFEM Solución analítica Razón Caso de carga Momento flector de cálculo MEd Armadura necesaria As,stat,tot Momento flector de cálculo MEd Armadura necesaria As,stat,tot MEd As,stat,tot [kNm] [cm2 ] [kNm] [cm2 ] [kNm] [cm2 ] CO7 1926,280 30,13 1927,000 33,10 0,99 0,91
'''Vano 2:'''
En este caso, no se considera la redistribución de momentos. La relación de redistribución de momentos se establece en 1,000.
En la literatura, la armadura longitudinal necesaria se determina utilizando métodos de aproximación para vigas en T según DAstb-heft 425. Usando este método, se supone que la fuerza de compresión en el ala está en el centro del ala (hf/2). en RFEM, la armadura necesaria se determina con un análisis de la sección. Esto da como resultado una armadura necesaria menor que en la bibliografía.Vano 2 RFEM Solución analítica Razón Caso de carga Momento flector de cálculo MEd Armadura necesaria As,stat,tot Momento flector de cálculo MEd Armadura necesaria As,stat,tot MEd As,stat,tot [kNm] [cm2 ] [kNm] [cm2 ] [kNm] [cm2 ] CO8 885,520 13,79 895,000 15,10 0,99 0,91
'''RFEM proporcionó la solución'''
Ahora, la redistribución del momento en el apoyo central se establece en un 15% en todas las combinaciones de carga. Los resultados se resumen en las tablas a continuación.
'''Apoyo A:'''
El caso de carga 8 entrega el momento flector más alto y, por lo tanto, es decisivo.
Apoyo A Caso de carga Momento flector de cálculo MEd Armadura necesaria As,stat,tot [kNm] [cm2 ] CO8 -1824.840 32,32
'''Apoyo B:'''
Apoyo B: Caso de carga Momento flector de cálculo MEd Armadura necesaria As,stat,tot [kNm] [cm2 ] CO4 -1345.890 22,40
'''Vano 1:'''
Cuando se considera la redistribución de momentos en todas las combinaciones de carga, CO5 tiene el momento flector de cálculo más alto en el vano 1.
Vano 1: Caso de carga Momento flector de cálculo MEd Armadura necesaria As,stat,tot [kNm] [cm2 ] CO5 2005,410 31,44
'''Vano 2:'''
CO8 tiene un momento de cálculo tras la redistribución del momento MEd de 940 kNm.
Vano 2: Caso de carga Momento flector de cálculo MEd Armadura necesaria As,stat,tot [kNm] [cm2 ] CO8 940,000 14,73
#'''Armadura de cortante'''
Armadura '''de cortante en el voladizo:'''
Para determinar los cercos necesarios en el voladizo, se examinan 3 posiciones. Los resultados se resumen en la siguiente tabla:
'''Vano 1:'''Voladizo Posición x Parámetro Símbolo Unidad RFEM Solución analítica Razón x = 0,45 m Canto útil d [m] 0,940 0,920 1,02 Brazo mecánico interior z [m] 0,848 0,828 1,02 esfuerzo cortante VEd [kN] -327.190 -328.000 0,99 Momento flector de cálculo MED [kNm] -73,320 -74.000 0,99 Componente de cortante de cálculo del esfuerzo en el área de compresión Vccd [kN] 12,550 13,000 0,99 Esfuerzo cortante de cálculo VEd,red [kN] 314,640 314,000 1,0 Capacidad a cortante sin armadura Vrd,cc [kN] 219,420 221,00 0,99 Inclinación de la biela comprimida cuna Θ [-] 3.0 3.0 1,0 Capacidad de la biela comprimida Vrd,máx. [kN] 996,230 1003,000 0,99 Armadura necesaria asw,nec [cm2/m] 2,84 2.91 0.98 x = 1,37 m Canto útil d [m] 1,070 1,050 1,02 Brazo mecánico interior z [m] 0,965 0,945 1,02 esfuerzo cortante VEd [kN] -417.720 -418.000 1.00 Momento flector de cálculo MED [kNm] -414.250 -415.000 1.00 Componente de cortante de cálculo del esfuerzo en el área de compresión Vccd [kN] 62,210 66,000 0,94 Esfuerzo cortante de cálculo VEd,red [kN] 355,510 353,000 1,01 Capacidad a cortante sin armadura Vrd,cc [kN] 250,070 252,000 0,99 Inclinación de la biela comprimida cuna Θ [-] 3.0 3.0 1,0 Capacidad de la biela comprimida Vrd,máx. [kN] 1135,860 1144,000 0,99 Armadura necesaria asw,nec [cm2/m] 2,83 2,86 0,99 x = 2,37 m Canto útil d [m] 1,210 1,190 1,02 Brazo mecánico interior z [m] 1,090 1,070 1,02 esfuerzo cortante VEd [kN] -541.800 -543.000 1,0 Momento flector de cálculo MED [kNm] -891.790 -893,00 1.00 Componente de cortante de cálculo del esfuerzo en el área de compresión Vccd [kN] 118,250 125,000 0,95 Esfuerzo cortante de cálculo VEd,red [kN] 423,550 418,000 1,01 Capacidad a cortante sin armadura Vrd,cc [kN] 283,220 285,000 0,99 Inclinación de la biela comprimida cuna Θ [-] 3.0 3.0 1,0 Capacidad de la biela comprimida Vrd,máx. [kN] 1286,410 1298,000 0,99 Armadura necesaria asw,nec [cm2/m] 2,98 2,99 1,0
La posición de la barra decisiva para el cálculo de los cercos en el campo 1 está a una distancia d del borde derecho del apoyo A.
'''Vano 2:''' El cálculo de los cercos se realiza de forma análoga al vano 1.Vano 1 Parámetro Símbolo Unidad RFEM Solución analítica Razón Canto útil d [m] 1,440 1,430 1.00 Esfuerzo cortante en el apoyo A VEd,A [kN] 1250,770 1250,000 1.00 Esfuerzo cortante de cálculo VEd,A,re [kN] 952,430 954,000 1.00 Capacidad a cortante sin armadura VRd,cc [kN] 346,210 343,000 1.00 Inclinación de la biela de compresión cuna Θ [-] 1.88 1,87 1.00 Armadura de cortante necesaria asw,nec [cm2/m] 8,95 9,11 0.98
Las diferencias en los resultados para el vano 2 se deben al hecho de que la bibliografía considera el esfuerzo cortante en el apoyo B después de la redistribución del momento. Sin embargo, la redistribución de momentos no influye en el cálculo del esfuerzo cortante en RFEM.Vano 2 Parámetro Símbolo Unidad RFEM Solución analítica Razón Canto útil d [m] 1,440 1,440 1,02 Esfuerzo cortante en el apoyo B VEd,B [kN] 886,580 855,000 1,03 Esfuerzo cortante de cálculo VEd,B,re [kN] 613,100 584,000 1.05 Capacidad a cortante sin armadura VRd,cc [kN] 346,210 343,000 1.00 Inclinación de la biela de compresión cuna Θ [-] 2.75 2.91 0,95 Armadura de cortante necesaria asw,nec [cm2/m] 3,94 3,58 1.10
.png?mw=600&hash=49b6a289915d28aa461360f7308b092631b1446e)
