Volver a los ejemplos
¿Le ha resultado útil esta página?
28x
009034
28-02-2025

VE0034 | Torsión de chapa delgada

Descripción del trabajo

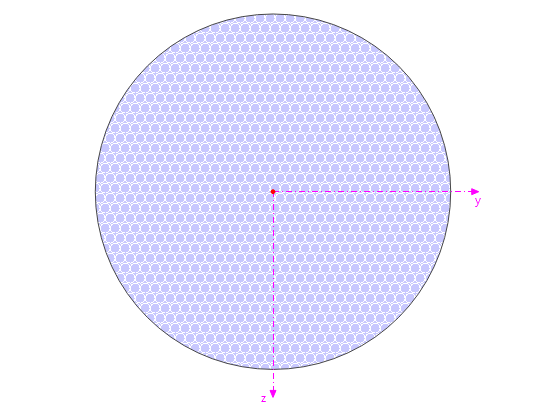
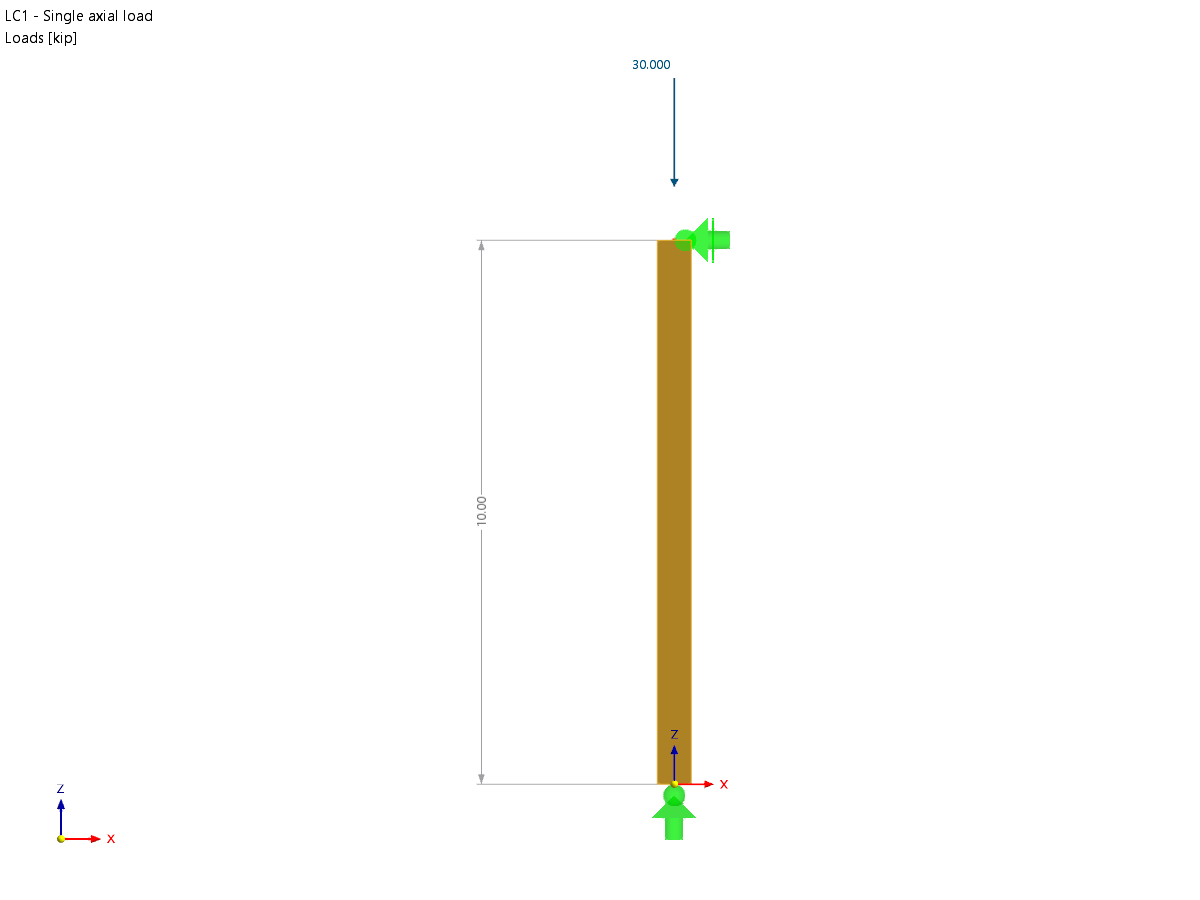
Una placa delgada está fija en un lado (φz = 0) y se carga por medio del par distribuido en el otro lado. Primero, la placa se modela como una superficie plana. Además, la placa se modela como un cuarto de la superficie del cilindro. El ancho del modelo plano' es igual a la longitud de un cuarto del círculo del modelo curvo. Por lo tanto, el modelo curvo tiene una constante de torsión J casi igual que el modelo plano. Determine el giro máximo de la placa φz,max para ambos modelos geométricos y compare los resultados utilizando la teoría de placas de Kichhoff y Mindlin.

Material Acero Módulo de elasticidad E 210000,000 MPa
coeficiente de Poisson ν 0,300 -
Geometría Radio del modelo curvo r 100,000 mm
Anchura del modelo plano s 157,080 mm
espesor de la losa h 200,000 mm
Altura de la chapa t 3,000 mm
Carga Par distribuido m 1268,720 Nm/m
Torsión de Placa Delgada
Torsión de Placa Delgada

Solución analítica

La constante de torsión para la placa plana (sección rectangular) se puede calcular según la siguiente fórmula:

J=st33=1413.720 mm4
Constante de torsión para la placa plana

Considerando el mismo ancho de la placa plana y curva, se puede usar la misma constante de torsión. El ancho de la placa plana es el mismo que la longitud de un cuarto del círculo del modelo curvo: s=πr/2. Las constantes de torsión de la placa plana y la placa curva también se comparan utilizando el programa SHAPE-THIN: Jp =1396.710mm4,Jc =1392,670mm4. Usando la constante de torsión, que se calcula en la fórmula mencionada anteriormente, se puede determinar el giro máximo en la parte superior de la placa (z = h) de la siguiente manera:

φz,max=mshGJ=0.349 rad=20.000°
Giro máximo en la parte superior de la chapa

Configuración de RFEM

  • Modelado en RFEM 5.26 y RRFEM 6.06
  • El tamaño del elemento es lFE = 0,002 m
  • Se considera el análisis geométricamente lineal
  • El número de incrementos es 5
  • Se usa la entidad de placa
  • Se utilizan elementos cuadrangulares

Resultados

Modelo Solución analítica RFEM 6 RFEM 5
φz,máx. [°] φz,máx. [°] Razón [-] φz,máx. [°] Razón [-]
Planar, Kirchhoff 20,000 20,163 1,008 20,163 1,008
Curva, Kirchhoff 20,163 1,008 20,163 1,008
Plano, Mindlin 20,666 1,033 20,733 1,037
Curvo, Mindlin 20,797 1,040 20,863 1,044
Ejemplo de verificación 0034 | 1
662x
17x
Ejemplo de verificación 0034 | 1
;
Vídeos
Modelos para descargar
Artículos de la base de datos de conocimientos
Formas básicas de estructuras de membranas [1]
Este artículo se centra en los aspectos específicos del diseño de estructuras de con membranas que tienen requisitos específicos, como la búsqueda de forma y la generación de patrones de corte. Una parte integral del diseño de estas estructuras es el proceso de encontrar formas pretensadas adecuadas y generar patrones de corte. El texto describe brevemente dos procesos básicos en el diseño de estructuras con membranas. Se explican los principios físicos y se ilustran las tesis individuales con ejemplos.
KB 001879 | Influencia de la rigidez a flexión de los cables
Este artículo describe y explica la influencia de la rigidez a flexión de los cables en sus esfuerzos internos. Además, el texto proporciona información sobre cómo se puede reducir esta influencia.
KB 001848 | Cálculo de pilares de madera según la norma NDS 2018 en RFEM 6
Con el complemento Timber Design, es posible diseñar pilares de madera según el método ASD estándar de 2018 NDS. El cálculo preciso de la capacidad de compresión de barras de madera y los factores de ajuste son importantes para las consideraciones de la seguridad y el diseño. El siguiente artículo verificará la resistencia crítica al pandeo máxima calculada por el complemento Timber Design utilizando ecuaciones analíticas paso a paso según la norma NDS 2018, incluidos los factores de ajuste de compresión, el valor de cálculo de compresión ajustado y la relación de cálculo final.
RWIND 2 es un programa para la generación de cargas de viento basado en CFD (Dinámica de Fluidos Computacional). La simulación numérica del flujo de viento se genera alrededor de cualquier edificio, incluidos los tipos de geometría irregular o única, para determinar las cargas de viento en las superficies y barras. RWIND 2 se puede integrar con RFEM/RSTAB para el análisis y dimensionamiento de estructuras o como una aplicación independiente.
Capturas de pantalla
Características de los productos
Característica 002423 | Representación de resultados en sólidos

Los resultados de las tensiones en sólidos se pueden mostrar como puntos coloreados en los elementos finitos.

Rendimiento de cálculo mejorado mediante la consideración optimizada de los grados de libertad en los nudos en RFEM

El número de grados de libertad en un nudo ya no es un parámetro de cálculo global en RFEM (6 grados de libertad para cada nudo de la malla en los modelos en 3D, 7 grados de libertad para el análisis de torsión de alabeo). Por lo tanto, cada nudo se considera generalmente con un número diferente de grados de libertad, lo que conduce a un número variable de ecuaciones en el cálculo.

Esta modificación acelera el cálculo, especialmente para los modelos donde se podría lograr una reducción significativa del sistema (por ejemplo, en cerchas y estructuras de membranas).

Visualización ampliada de deformaciones en superficies

Muestre las deformaciones ampliadas de barras, superficies y sólidos (por ejemplo, deformaciones principales importantes, las deformaciones totales equivalentes, etc.) en el Navegador de proyectos - Resultados en RFEM y en la Tabla 4.0.

Por ejemplo, puede mostrar las deformaciones plásticas determinantes al realizar el diseño plástico de conexiones con elementos de superficies.

Exportar modelos de RFEM o RSTAB al formato * .glb o * .glTF

Los modelos de RFEM y RSTAB se pueden guardar como modelos glTF en 3D (formatos *.glb y *.glTF). Vea los modelos en 3D en detalle con un visor 3D de Google o Babylon. Lleve sus gafas de realidad virtual (VR), como Oculus, para "caminar" a través de la estructura.

Puede integrar los modelos glTF en 3D en sus propios sitios web utilizando JavaScript según estas instrucciones (como en la web de Dlubal - Modelos para descargar): "Represente fácilmente modelos 3D interactivos en la web y en realidad aumentada" .

Preguntas más frecuentes (FAQs)

¿Dónde puedo encontrar los informes de actualización de RFEM 5, RSTAB 8, SECCIÓN, E-SECCIONES, RX-TIMBER, PUENTE GRÚA, PANELES, COMPOSITE?

Para mi tarjeta gráfica NVIDIA, tengo la opción entre un controlador del "Production Branch" o del "New Feature Branch". ¿Qué controlador es más adecuado para RFEM/RSTAB?
¿Es posible evaluar rápidamente si la malla utilizada es lo suficientemente fina?
¿Por qué los valores mínimos y máximos del desplazamiento total no coinciden con las deformaciones cuando se trabaja con combinaciones de resultados?

¿Por qué recibo un mensaje de error sobre un material no válido al definir superficies de madera?
¿RFEM 5 tiene el contacto de superficies?
Proyectos de clientes