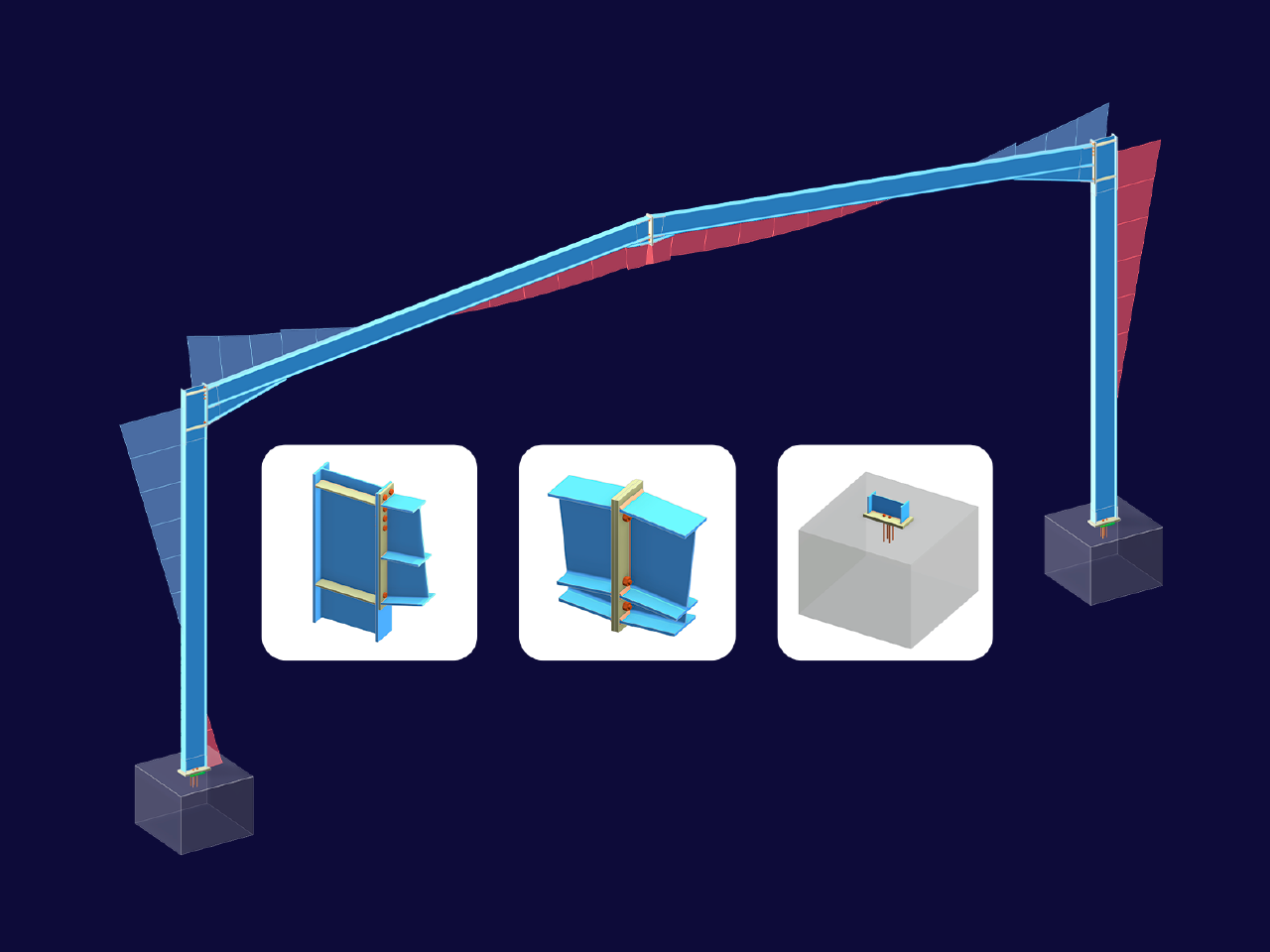
Le modèle de cet article technique est basé sur un système avec gousset sur un poteau, décrit en détail à la page 8.67 de l'ouvrage [1] issu de la littérature spécialisée.
Système
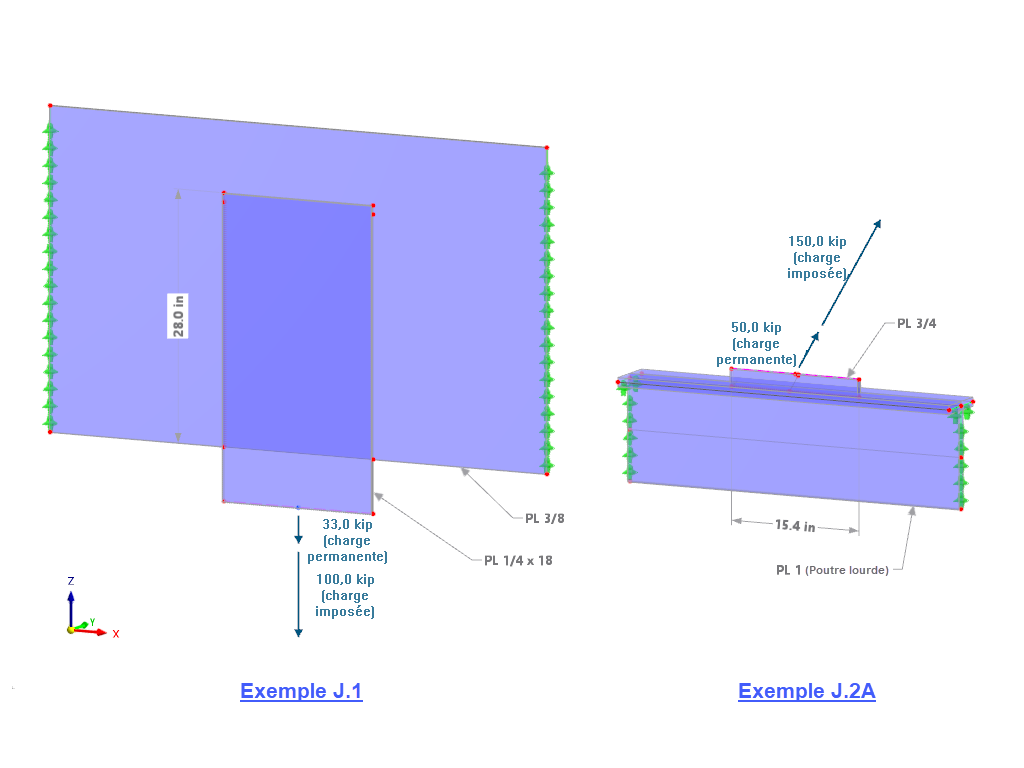
Ce système est composé d'un poteau HEB 140 à la semelle duquel un gousset doit être soudé à l'aide d'une double soudure d'angle. Le poteau est ainsi connecté à une barre de traction, qui est ignorée dans cet exemple. Une charge de 330 kN est appliquée et répartie sur les trois trous correspondants aux vis du système. Bien que la charge soit connue ici, les efforts requis doivent être déterminés à partir des efforts internes du gousset. La charge est utilisée à des fins de vérification seulement.
Détermination de la résultante des efforts
La formule de la résultante des efforts est celle du tableau 8.66c de [1].
Les différents composants d'effort peuvent être calculés comme suit :
Les efforts F ainsi que le moment peuvent être déterminés en définissant une coupe. Seul le gousset doit être considéré dans la boîte de dialogue de la coupe.
Méthode 1
Après le calcul, vous pouvez afficher graphiquement les résultantes de la coupe de chaque section.
Ces valeurs peuvent ensuite être utilisées dans les formules correspondantes. L'affectation des résultantes des efforts est la suivante pour cet exemple.
F1⊥, Ed = PX = 165,37 kN
F2⊥, Ed = PY = 0 kN
Fll, Ed = PZ = 285,95 kN
MEd = MY = 8,38 kNm
Les résultantes de coupe étant disposées de la même manière que les axes globaux, il est nécessaire de modifier les résultats pour les soudures ou les coupes positionnées différemment afin d'obtenir les efforts et les moments correspondants. Par conséquent, une autre méthode est appliquée.
Méthode 2
La coupe déjà créée peut également être à nouveau utilisée. Le diagramme de résultats correspondant est ouvert pour poursuivre l'analyse.
En considérant le système d'axes local de la surface, les efforts internes de base vx (= 0, car pas de charges horizontales), nx et nxy sont affichés. L'interprétation des résultats des diagrammes permet également les efforts requis. Un calcul supplémentaire est nécessaire, mais uniquement pour déterminer le moment. Pour ce faire, les valeurs intermédiaires de l'effort interne de base nx sont exportées vers Excel. Le moment résulte de la somme des efforts des différents segments multipliée par la distance correspondante jusqu'au centre de la coupe.
Les résultats obtenus grâce aux deux méthodes sont identiques. Une brève vérification en décomposant l'effort de 330 kN appliqué à un angle de 30° permet également d'obtenir les paires d'efforts ainsi que le moment de :
F⊥, Ed = 330 ⋅ sin 30 ° = 165 kN
Fll, Ed = 330 ⋅ cos 30 ° = 285 kN
MEd = 165 ⋅ 0,05 = 8,3 kNm
Vérification de la soudure d'angle
La résultante des efforts peut maintenant être déterminée à l'aide des efforts et du moment.
N⊥, Ed = 165/34 + 8,38/(34²/6) = 9,20 kN/cm
V⊥, Ed = 0
Vll, Ed = 286/34 = 8,41 kN/cm
Fw, Ed = √ 9,2² + 8,41² = 12,46 kN/cm
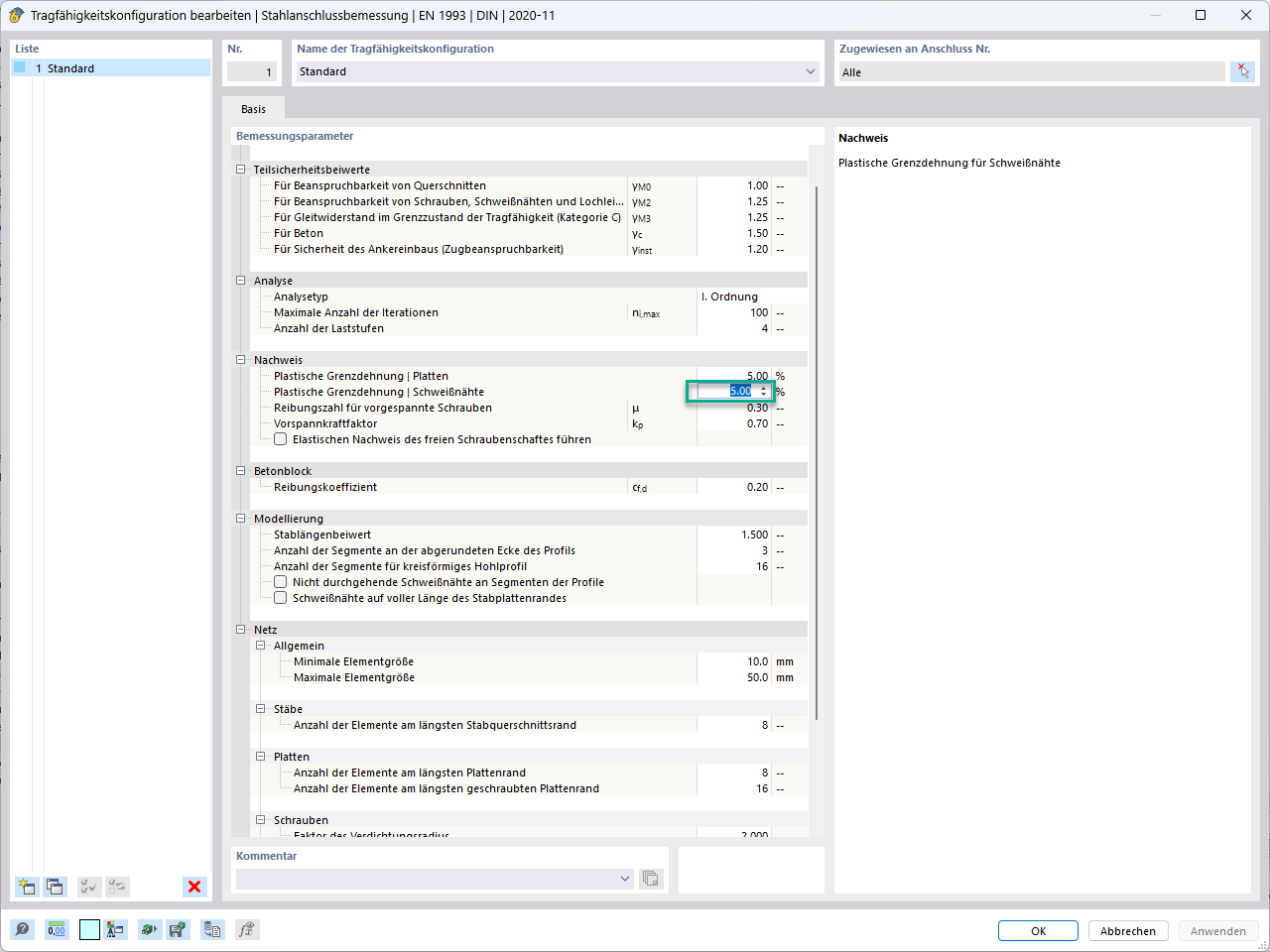
Elle est finalement comparée à la valeur de calcul de la résistance de la soudure d'angle. La soudure d'angle est supposée faire 3 mm d'épaisseur.
Fw, Rd = (36/√ 3 ⋅ 0,8 ⋅ 1,25) ⋅ 2 ⋅ 0,3 = 12,47 kN/cm
Fw, Ed = 12,46 kN/cm <Fw, Rd = 12,47 kN/cm
Dlubal_KohlA_Rev1.png?mw=350&hash=f8d2ccd6ebb5a4c58d1c98f433e9f5171a41f581)
.png?mw=600&hash=49b6a289915d28aa461360f7308b092631b1446e)
