5760x

001650

Dipl.-Ing. (FH) Lukas Sühnel

2020-08-05

从有限元模型中计算得出结果，以便进行简化的焊缝设计

欧洲规范 EN 1993-1-8 章节 4.5.3.3。为用户提供了一种简化的角焊缝承载能力极限状态设计方法。根据规范，如果角焊缝区域的合力的设计值小于焊缝承载力的设计值，则满足设计要求。由于有限元计算的特性，如果您想对面模型中的焊缝尺寸进行标注，将会得到不同的结果。因此，我们在下文中将介绍如何从模型中确定分力。

本技术文章中的模型是基于柱子节点板体系，更多详细信息请参见 [1] 书第 8.67 页。

系统

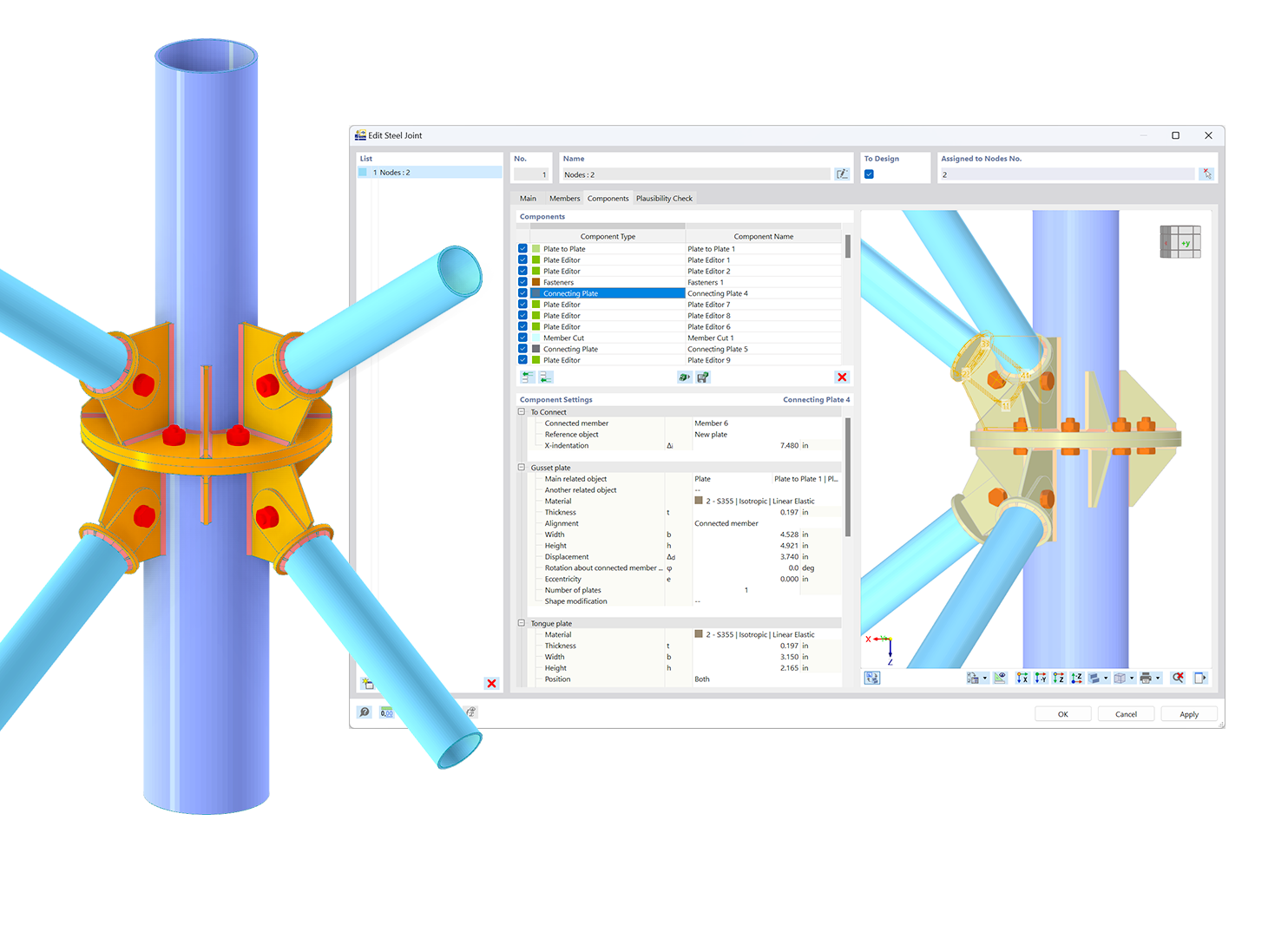
Grundlegend besteht das System aus einer Stütze HEB 140, an deren Flansch ein Knotenblech mittels einer Doppelkehlnaht angeschweißt werden soll. Dieses verbindet die Stütze mit einem Zugstab, welcher hier jedoch unbeachtet bleiben soll. Die einwirkende Last beträgt 330 kN und wird auf die drei Schraubenlöcher verteilt in das System eingetragen. Obgleich die Last hier bekannt ist, soll die Bestimmung der benötigten Kräfte aus den Schnittgrößen des Knotenbleches erfolgen. Die Last dient nur der gedanklichen Kontrolle.

1 System mit lokalem Achsensystem des Knotenbleches

Bestimmung der Kraftresultierenden

Die Formel für die Kraftresultierende wird aus Tafel 8.66c in [1] entnommen.

F_{w, Ed} = \sqrt{({N^{2}}_{⊥, Ed} + {V^{2}}_{⊥, Ed} + {V^{2}}_{∥, Ed})}

Kraftresultierende

Die einzelnen Kraftkomponenten können wie folgt berechnet werden.

N_{⊥, Ed} = \frac{F_{1 ⊥, Ed}}{l_{w}} \pm \frac{M_{Ed}}{(\frac{l_{w}^{2}}{6})}

V_{⊥, Ed} = \frac{F_{2 ⊥, Ed}}{l_{w}}

V_{∥, Ed} = \frac{F_{∥, Ed}}{l_{w}}

力分量

Die Kräfte F sowie das Moment können mittels der Definition eines Schnittes bestimmt werden. Dabei sollte im Dialog des Schnittes nur das Knotenblech betrachtet werden.

2 截面定义

方法 1

Nach erfolgter Berechnung kann man sich grafisch die Schnittresultierenden für jeden Schnitt ausgeben lassen.

3 Resultierende Kräfte und Momente des Schnittes

Diese Werte können nun in die entsprechenden Formeln eingesetzt werden. Die Zuordnung der Resultierenden zu den Kräften sieht in diesem Beispiel wie folgt aus.

F_1⊥,Ed = P_X = 165, 37 kN
F_2⊥,Ed = P_Y = 0 kN
F_ll,Ed = P_Z = 285, 95 kN
M_Ed = M_Y = 8, 38 kNm

Da die Schnittresultierenden analog der globalen Achsen angeordnet sind, wären bei anderweitig liegenden Schweißnähten beziehungsweise Schnitten weitere Ergebnistransformationen nötig, um die entsprechenden Kräfte und Momente zu erhalten. Es soll daher noch eine weitere Methode aufgezeigt werden.

方法 2

Auch hierfür kann der bereits angelegte Schnitt verwendet werden. Für die weitere Auswertung wird der zugehörige Ergebnisverlauf geöffnet.

4 Resultierende Kräfte und Momente des Schnittes

Unter Beachtung des lokalen Flächen-Achsen-Systems werden die Grundschnittgrößen v_x (= 0, da keine horizontalen Lasten), n_x sowie n_xy dargestellt. Die Ergebnisinterpretation der Verläufe liefert erneut die benötigten Kräfte. Einzig für die Bestimmung des Momentes bedarf es einer weiteren Berechnung. Hierzu werden die Zwischenwerte der Grundschnittgröße n_x nach Excel exportiert. Das Moment ergibt sich dann aus der Summe der Kräfte der einzelnen Segmente multipliziert mit dem zugehörigen Abstand bis zur Mitte des Schnittes.

5 Ergebniswerte des Schnittes

Die Ergebnisse der beiden Methoden sind identisch. Eine gedankliche Überprüfung mittels der Zerlegung der im Winkel von 30 ° angreifenden Kraft von 330 kN ergibt ebenfalls die Kräftepaare sowie das Moment von:
F_⊥,Ed = 330 ⋅ sin 30 ° = 165 kN
F_ll,Ed = 330 ⋅ cos 30 ° = 285 kN
M_Ed = 165 ⋅ 0,05 = 8, 3 kNm

Nachweis der Kehlnaht

Mittels der Kräfte sowie des Momentes kann nun die Kraftresultierende bestimmt werden.
N_⊥,Ed = 165 / 34 + 8, 38 / ( 34² / 6 ) = 9, 20 kN/cm
V_⊥,Ed = 0
V_ll,Ed = 286 / 34 = 8, 41 kN/cm
F_w,Ed = √ 9, 2² + 8, 41² = 12, 46 kN/cm

Diese wird final dem Bemessungswert der Tragfähigkeit der Kehlnaht gegenüber gestellt. Die Kehlnahtdicke wird hierbei mit 3 mm angenommen.